Question

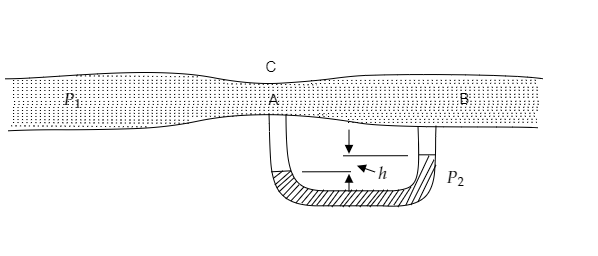
A fluid of density ${\rho _1}$ is flowing through a tube of varying cross-section. A manometer containing a liquid of density ${\rho _2}$ is connected to the tube as shown. The area of cross-section of the tube at point A and B are ${a_1}$ and ${a_2}$ respectively. Find the rate of flow of the liquid through the tube.

A) ${a_1}{a_2}\sqrt {\dfrac{{2{\rho _2}gh}}{{{\rho _1}\left( {{a_2}^2 - {a_1}^2} \right)}}} $
B) ${a_1}{a_2}\sqrt {\dfrac{{2gh}}{{{\rho _1}\left( {{a_2}^2 - {a_1}^2} \right)}}} $
C) $\dfrac{{{a_1}}}{{{a_2}}}\sqrt {\dfrac{{2{\rho _2}gh}}{{{\rho _1}\left( {{a_2}^2 - {a_1}^2} \right)}}} $
D) ${a_1}{a_2}\sqrt {\dfrac{{2{\rho _1}gh}}{{{\rho _2}\left( {{a_2}^2 - {a_1}^2} \right)}}} $

Answer 1

Hint: The given tube has different cross-sectional areas at A and B. So the velocity of the liquid at A and B will also differ. But the mass flowing through A will be the same as that flowing through B. Flow rate refers to the amount of liquid flowing through a given area. Bernoulli’s equation for regions A and B will help us determine the flow rate of the liquid through the tube.

Formulae used:
Bernoulli’s equation is given by, ${P_1} + \dfrac{{\rho {v_1}^2}}{2} + \rho g{h_1} = {P_2} + \dfrac{{\rho {v_2}^2}}{2} + \rho g{h_2}$ where ${P_1}$ , ${P_2}$ are the pressures at two different sections of a tube, $\rho $ is the density of the fluid, ${v_1}$ , ${v_2}$ are the velocities of the fluid at the two different sections, $g$ is the acceleration due to gravity and ${h_1}$ , ${h_2}$ are the heights from the ground.
The equation of continuity is given by, ${A_1}{v_1} = {A_2}{v_2}$ where ${A_1}$ , ${A_2}$ are the area at two different regions of a tube and ${v_1}$ , ${v_2}$ are the velocities at these two regions.

Complete step by step answer:
The density of the liquid flowing through the given tube is given to be ${\rho _1}$ .
The density of the liquid in the manometer is given to be ${\rho _2}$ .
The cross-sectional area of the tube at A is given to be ${a_1}$ while that at B is given to be ${a_2}$ .
Let ${P_A}$ and ${P_B}$ be the pressure of the liquid at A and B.
Let ${v_1}$ and ${v_2}$ be the velocity of the liquid at A and B.
Express Bernoulli's equation for the regions A and B.
Bernoulli’s equation for regions A and B can be expressed as ${P_A} + \dfrac{{{\rho _1}{v_1}^2}}{2} = {P_B} + \dfrac{{{\rho _1}{v_2}^2}}{2}$ .
$ \Rightarrow {P_A} - {P_B} = \dfrac{{{\rho _1}}}{2}\left( {{v_2}^2 - {v_1}^2} \right)$ -------- (1)
The pressure difference at A and B as given by the manometer will be ${P_A} - {P_B} = {\rho _2}gh$ ------- (2)
Substituting equation (2) in (1) we get, ${\rho _2}gh = \dfrac{{{\rho _1}}}{2}\left( {{v_2}^2 - {v_1}^2} \right)$
$ \Rightarrow \left( {{v_2}^2 - {v_1}^2} \right) = \dfrac{{2{\rho _2}gh}}{{{\rho _1}}}$ ----------- (3)
Using the continuity equation at A and B express the velocity at A.
As the area and velocity of the liquid at A are ${a_1}$ , ${v_1}$ and that at B are ${a_2}$ , ${v_2}$ , the continuity equation for A and B can be expressed as ${a_1}{v_1} = {a_2}{v_2}$ .
$ \Rightarrow {v_2} = \dfrac{{{a_1}{v_1}}}{{{a_2}}}$ --------- (4)
Substituting equation (4) in (3) we get, ${\left( {\dfrac{{{a_1}{v_1}}}{{{a_2}}}} \right)^2} - {v_1}^2 = \dfrac{{2{\rho _2}gh}}{{{\rho _1}}}$
On simplifying this becomes $\dfrac{{{a_1}^2{v_1}^2 - {a_2}^2{v_1}^2}}{{{a_2}^2}} = \dfrac{{2{\rho _2}gh}}{{{\rho _1}}}$ or ${v_1}^2 = \dfrac{{{a_2}^2}}{{\left( {{a_1}^2 - {a_2}^2} \right)}}\left( {\dfrac{{2{\rho _2}gh}}{{{\rho _1}}}} \right)$
$ \Rightarrow {v_1} = {a_2}\sqrt {\dfrac{{2{\rho _2}gh}}{{{\rho _1}\left( {{a_1}^2 - {a_2}^2} \right)}}} $
Express the flow rate of the liquid at A.
The flow rate of the liquid at A will be the flow rate of the liquid through the tube.
Then the flow rate of the liquid is expressed as $Q = {a_1}{v_1}$ -------- (5)
Substituting for ${v_1} = {a_2}\sqrt {\dfrac{{2{\rho _2}gh}}{{{\rho _1}\left( {{a_1}^2 - {a_2}^2} \right)}}} $ in equation (5) we get, $Q = {a_1}{a_2}\sqrt {\dfrac{{2{\rho _2}gh}}{{{\rho _1}\left( {{a_1}^2 - {a_2}^2} \right)}}} $
Thus we obtain the flow rate of the liquid as $Q = {a_1}{a_2}\sqrt {\dfrac{{2{\rho _2}gh}}{{{\rho _1}\left( {{a_1}^2 - {a_2}^2} \right)}}} $ .

So the correct option is A.

Note: The manometer is an instrument that is used to determine the pressure of a tube which has a U-shape similar to the given tube. As the pressure of the liquid at A and B are different, the liquid in the manometer will reach two different heights as shown in the figure. The pressure difference between A and B is then obtained as the potential energy per unit volume of the liquid in the manometer and it is given by equation (2).