Question

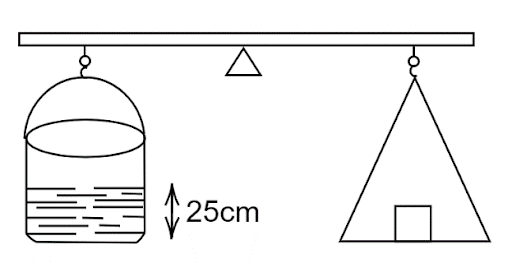
A cylinder containing water up to a height of 25 cm has a hole of cross-section \[\dfrac{1}{4}{\rm{c}}{{\rm{m}}^{\rm{2}}}\]in its bottom. It is counterpoised in a balance. What is the initial change in the balancing weight when water begins to flow out?

A. Increases of 12.5gm-wt
B. Increases of 6.25gm-wt
C. Decreases of 12.5gm-wt
D. Decreases of 6.25gm-wt

Answer 1

Hint:Before we start addressing the problem, we need to know about what data has been provided and what we need to solve. Here they have given the height of water in a cylinder, and the cross-sectional area of a cylinder. We need to find the initial change in the balancing weight, whether it is decreasing or increasing. In order to see that let’s look into the following steps.

Formula Used:
To find the weight of an object we have,
\[F = wg\]
\[ \Rightarrow w = \dfrac{F}{g}\]
Where, F is the force and G is acceleration due to gravity.

Complete step by step solution:

Image: Weighing of a cylinder containing water.

Consider the cylinder in which the water begins to flow out at velocity v and having the area of cross section A. Then the volume flow rate is given by,
\[V = Av\]
The mass flow rate is written as,
\[m = V \times \rho \]…………….. (1)
Now, substitute the value of volume in the above equation we get,
\[m = Av \times \rho \]
We know that, \[v = \sqrt {2gh} \]
Then substitute the above value in equation (1) we obtain
\[m = A\sqrt {2gh} \times \rho \]…… (2)

Now, the momentum is given by,
\[P = mv\]………… (3)
Put the value of equation (2) in (3) we obtain,
\[P = A\sqrt {2gh} \times \rho v\]
From equation (3), the rate of change of momentum can be written as,
\[\dfrac{{dP}}{{dt}} = \dfrac{{dm}}{{dt}}v\]

We know that \[\dfrac{{dm}}{{dt}}\] is the mass flow rate, and \[\dfrac{{dP}}{{dt}}\] is force then,
\[F = Av\rho \times v\]
\[\Rightarrow F = A{v^2}\rho \]
\[ \Rightarrow F = A\left( {2gh} \right)\rho \]
In order to find the weight, we have,
\[F = wg\]
\[ \Rightarrow w = \dfrac{F}{g}\]
Put the value of equation (4) in above equation, we get
\[ \Rightarrow w = A\left( {2h} \right)\rho \]

Now substitute the values of area is \[\dfrac{1}{4}{\rm{c}}{{\rm{m}}^{\rm{2}}}\] height is 25cm and density of water is \[{\rm{1gm/}}{{\rm{m}}^{\rm{3}}}\] in above equation we get,
\[ \Rightarrow w = \dfrac{1}{4}\left( {2 \times 25} \right) \times 1\]
\[ \Rightarrow w = 12.5gm - wt\]
When the water begins to flow out, then the net upward reaction force decreases because the weight of the water in the cylinder decreases thereby decreasing the balancing weight. Therefore, the initial change in the balancing weight when water begins to flow out decreases by 12.5gm-wt.

Hence, option C is the correct answer.

Note:While calculating don’t get confused with the mass and the rate of flow of mass, as rate of mass refers to the flow of mass per unit time and convert every unit into S.I unit at last.