Question

A convex mirror has a focal length $f$. A real object is placed at a distance $f$ in front of it from the pole produces an image at:
A) $\infty $
B) $f$
C) $\dfrac{f}{2}$
D) $2f$

Answer 1

Hint: To solve this question we have to use mirror formulae. Also, for a convex mirror, the focal length is on the painted side. So it is considered positive while the object distance is considered negative.

Formulae used:
$\dfrac{1}{f} = \dfrac{1}{v} + \dfrac{1}{u}$
Here $f$ is the focal length for the mirror, $v$ is the distance of image from the pole and $u$ is the distance of the object from the pole.

Complete step by step answer:
In the question, a convex mirror is given. It is said that it has a focal length of $f$ and the object is kept at $f$ distance in front of the image.
Let’s see the diagram of a convex mirror.

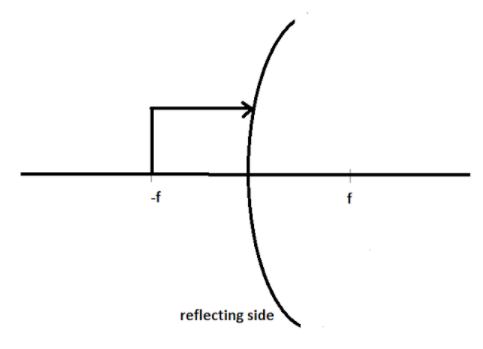
We know that all the distance in the direction of the light source is considered positive whereas the distance in the opposite directions is considered negative. So for a convex mirror, the focal length is considered positive as it is on the non-reflecting side of the mirror i.e. in the direction of the light source. As the object is present in the opposite direction of the light source, its distance is considered negative. Here,
Focal length =$f$ and
Object distance = $ - f$
Applying the mirrors formulae,
$ \Rightarrow \dfrac{1}{f} = \dfrac{1}{v} + \dfrac{1}{u}$
Here $f$ is the focal length for the mirror, $v$ is the distance of the image from the pole and $u$ is the distance of the object from the pole.
Substituting the values of focal length and object distance, we get
$ \Rightarrow \dfrac{1}{f} = \dfrac{1}{v} + \dfrac{1}{{ - f}}$
$ \Rightarrow \dfrac{1}{v} = \dfrac{1}{f} + \dfrac{1}{f}$
$ \Rightarrow \dfrac{1}{v} = \dfrac{2}{f}$
$ \therefore v = \dfrac{f}{2}$
So the answer will be $\dfrac{f}{2}$ in the direction of the light source i.e. on the non-reflecting side of the mirror.

Hence option (C) is the answer.

Note: Always use the mirror formulae after proper use of signs. The positive or negative signs should be given according to their direction from the light source. The one which is in the backward direction of the light source should be given negative signs and the one which is in the direction of the light source is considered positive.