Question

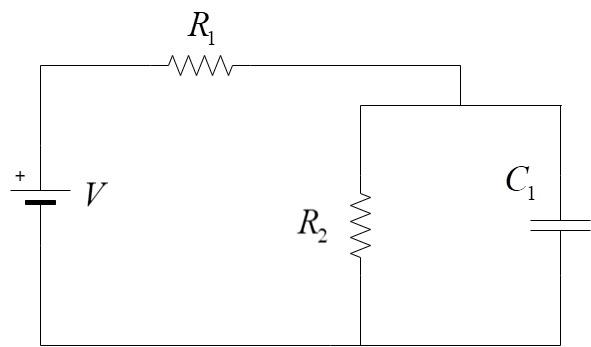
A Circuit contains two identical resistors of resistance R and a capacitor of capacitance ${C_1}$ connected to a battery that provides an emf of V, as shown above. At time zero, the Capacitor is initially uncharged. Which of the following expressions would represent the power dissipated in the resistor ${R_2}$ ​at time zero?

A) 0
B) $\dfrac{1}{{{e^{RC}}}}$
C) $\dfrac{{{V^2}}}{R}$
D) $\dfrac{{{V^2}}}{{2R}}$

Answer 1

Hint: In capacitor at time equal to zero there will be no current flowing and will also be equal to zero hence charge also be zero. When connected to a battery of emf V the capacitor will get charged and through the formula of V=IR we will get the value of current and then P=${I^2}R$ for power dissipated in R.

Complete step by step solution:
Step 1:
Let us know about the capacitor first before solving the question:
 A capacitor (originally known as a condenser) is a passive two-terminal electrical component used to store energy electro statically in an electric field. The forms of practical capacitors vary widely, but all contain at least two electrical conductors (plates) separated by a dielectric (i.e. insulator).
The starting capacitor works by accumulating a large electrical charge inside the capacitor. During compressor or other motor startup, the start capacitor releases its charge to give a voltage "boost" to get the electric motor spinning.

Step 2:
Coming to the question:
A Circuit contains two identical resistors of resistance R and a capacitor of capacitance ${C_1}$ connected to a battery that provides an emf of V
At time zero, the Capacitor is initially uncharged.
At time t=0 there will zero charge in the capacitors, which is q=0
After a long time steady state is reached, now the voltage across capacitor is constant (equal to the voltage of battery) hence current becomes zero
The total resistance across the capacitor is ${R_1} + {R_2}$
Now from the formula of $V$ = $IR$ we can find the current across the capacitor
Therefore, $I$ = $\dfrac{V}{{{R_{TOTAL}}}}$ $ \Rightarrow \dfrac{V}{{{R_1} + {R_2}}}$
Or we can write current I=$\dfrac{V}{{2R}}$ as resistance is same (given in question)
The formula for power dissipated is P=${I^2}R$
So, the power dissipated in resistor ${R_2}$​at time zero is P=${\left( {\dfrac{V}{{2R}}} \right)^2}R$ which is equal to $\dfrac{{{V^2}}}{{2R}}$

Hence, the correct option is Option D.

Additional information:
Capacitors have many important applications. They are used, for example, in digital circuits so that information stored in large computer memories is not lost during a momentary electric power failure; the electric energy stored in such capacitors maintains the information during the temporary loss of power.
Capacitors (sometimes known as condensers) are energy-storing devices that are widely used in televisions, radios, and other kinds of electronic equipment. Tune a radio into a station, take a flash photo with a digital camera, or flick the channels on your HDTV and you're making good use of capacitors.

Note: The students should not assume that the capacitance of a conductor depends on the charge and voltage. The capacitance of a conductor is a property of a material which is given by the formula – $C = \dfrac{{{\varepsilon _0}A}}{d}$
where ${\varepsilon _0}$ is the permittivity, A is the area of the two conductors and d = the distance of separation between the two conductors.