Question

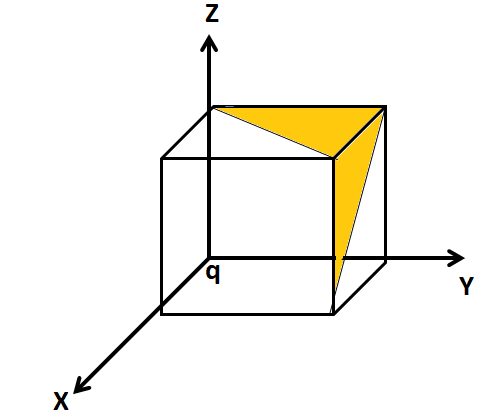
A charge ‘\[q\]’ is placed at one corner of a cube as shown in the figure. The flux of electrostatic field \[\vec E\] through the shaded area is:

A. \[q/48{\varepsilon _0}\]
B. \[q/8{\varepsilon _0}\]
C. \[q/24{\varepsilon _0}\]
D. \[q/4{\varepsilon _0}\]

Answer 1

Hint: In this question, we need to find the flux of electrostatic field \[\vec E\] through the shaded area. For this, the total flux through the cube and the total flux through one outer face of the cube. With the help of this, we have to find the total flux through the shaded area.

Complete step by step solution:
Consider the following figure.

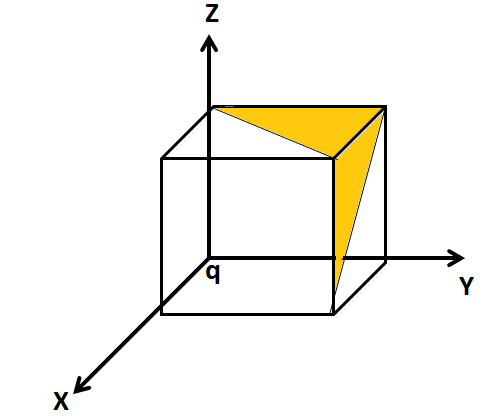
We know whenever a charge q is positioned at the cube-corner; it is distributed evenly by eight cubes.
The total flux through the cube is given by,
\[{T_C} = \left( {q/{\varepsilon _0}} \right) \times \dfrac{1}{8}\]
\[{T_C} = \dfrac{q}{{8{\varepsilon _0}}}\]
However, there is only flux across three faces.
Thus, the total flux through one external face of the cube \[ = \left( {\dfrac{q}{{8{\varepsilon _0}}}} \right) \times \dfrac{1}{3}\]

This gives the total flux through one external face of the cube \[ = \left( {\dfrac{q}{{24{\varepsilon _0}}}} \right)\]
So, the total flux through shaded region is given by,
\[{T_S} = \left( {\dfrac{q}{{24{\varepsilon _0}}} + \dfrac{q}{{24{\varepsilon _0}}}} \right) \times \dfrac{1}{2}\]
By simplifying, we get
\[{T_S} = \dfrac{q}{{24{\varepsilon _0}}}\]
Here, half of every face is shaded by a cube.

Therefore, the correct option is (C).

Additional Information: We can say that the electric flux is described as the tally of the amount of electric field lines that penetrate a region. Here, the electric field lines are thought to start with positive charges and end with negative charges. We can denote it mathematically as \[\phi = E \times A\] where, \[\phi ,E\] and \[A\] are the electric flux, magnitude of electric field and area of the surface through which the electric flux is to be determined respectively.

Note: Many students make mistakes in finding the total flux through the shaded region. Also, we may get false results due to wrong calculations. This is the only way through which we can solve this example in a simplified way.