Question

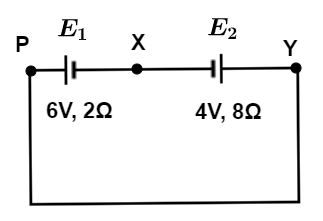
A cell ${E_1}$ of emf $6V$ and internal resistance $2\Omega $ is connected with another cell ${E_2}$ ​ of emf $4V$ and internal resistance $8\Omega $ (as shown in the figure). The potential difference across points X and Y is:

(A) $3.6V$
(B) $10V$
(C) $5.6V$
(D) $2V$

Answer 1

Hint: In order to solve this question, firstly we will find the net resistance and emf of the circuit to calculate the current in the circuit, and then using the general relation between emf, current, and resistance, we will solve for the potential difference between two points X and Y.

Formula Used:
$V = E + IR$
Where,
E-The emf of the battery,
R- The resistance
I-The current flowing into the battery and
V-The potential difference across the two points including the battery

Complete answer:
We have given that, cell ${E_1}$ of emf 6V and internal resistance $2\Omega $ is connected with another cell ${E_2}$ ​ of emf $4V$ and internal resistance $8\Omega $, let us assume that ‘I’ be the current flowing in the circuit as shown in the below figure,

Now, the net emf of two batteries is
\[
  E = {E_1} - {E_2} \\
  E = 6 - 4 \\
  E = 2V \\
 \]

The net resistance of series combination of the circuit is
$
  R = {R_1} + {R_2} \\
  R = 8 + 2 \\
  R = 10\Omega \\
 $

So, Current I flowing in the circuit is given by $I = \dfrac{E}{R}$ on putting the required values, we get
$
  I = \dfrac{2}{{10}} \\
  I = 0.2A \\
 $

Now, Between the points X and Y the emf of the battery is ${E_2} = 4V$ ,resistance between points X and Y is ${R_2} = 8\Omega $ and current is $I = 0.2A$ let V be the potential difference across pints X and Y then using formula, $V = E + IR$ we get
$
  V = 4 + (0.2)8 \\
  V = 4 + 1.6 \\
  V = 5.6 \\
 $

So, The potential difference between points X and Y is 5.6V

Hence, the correct option is (C) 5.6V.

Note: It should be remembered that the equation $V = E + IR$ is used because the current is entering into the battery if current were leaving the battery then the equation $V = E - IR$ will be used and in a series combination of resistances same current flows in every resistance of the circuit.