Question

A body moves along an uneven surface with constant speed at all points. The normal reaction of the road on the body is:


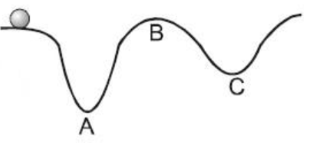
A) maximum at A
B) maximum at B
C) minimum at C
D) the same at A, B & C

Answer 1

Hint: For any question type where the normal reaction of the body is asked then start the question by making FBD (free body diagram) as it facilitates the further solution in a smooth manner.

Complete step by step solution:
Free body diagram is given as


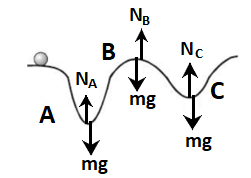
Let us consider that the body is moving with constant velocity v.
For A:
The body exerts a force (action) equal to the weight W=mg on the surface. The surface exerts a reaction NA on the body in equal direction.
Here, the centripetal force (${{\text{F}}_{\text{C}}}{\text{ = }}\dfrac{{{\text{m}}{{\text{v}}^{\text{2}}}}}{{{{\text{R}}_{\text{A}}}}}$) is in upward direction.
Net force is given by
$ {{\text{N}}_{\text{A}}}{\text{ - mg = }}\dfrac{{{\text{m}}{{\text{v}}^{\text{2}}}}}{{{{\text{R}}_{\text{A}}}}} \\
   \Rightarrow {{\text{N}}_{\text{A}}}{\text{ = }}\dfrac{{{\text{m}}{{\text{v}}^{\text{2}}}}}{{{{\text{R}}_{\text{A}}}}}{\text{ + mg}}...{\text{(i)}} \\
$
Where ${{\text{N}}_{\text{A}}}$= Normal reaction

For B:
The body exerts a force (action) equal to the weight W=mg on the surface. The surface exerts a reaction NB on the body in equal direction.
Here, the centripetal force (${{\text{F}}_{\text{C}}}{\text{ = }}\dfrac{{{\text{m}}{{\text{v}}^{\text{2}}}}}{{{{\text{R}}_{\text{B}}}}}$) is in downward direction.
Net force is given by
$ {\text{mg - }}{{\text{N}}_{\text{B}}}{\text{ = }}\dfrac{{{\text{m}}{{\text{v}}^{\text{2}}}}}{{{{\text{R}}_{\text{B}}}}} \\
   \Rightarrow {{\text{N}}_{\text{B}}}{\text{ = mg - }}\dfrac{{{\text{m}}{{\text{v}}^{\text{2}}}}}{{{{\text{R}}_{\text{B}}}}}...{\text{(ii)}} \\
$

For C:
The body exerts a force (action) equal to the weight W=mg on the surface. The surface exerts a reaction NC on the body in an equal direction.
Here, the centripetal force (${{\text{F}}_{\text{C}}}{\text{ = }}\dfrac{{{\text{m}}{{\text{v}}^{\text{2}}}}}{{{{\text{R}}_{\text{C}}}}}$) is in downward direction.
Net force is given by
$ {{\text{N}}_{\text{C}}}{\text{ - mg = }}\dfrac{{{\text{m}}{{\text{v}}^{\text{2}}}}}{{{{\text{R}}_{\text{C}}}}} \\
   \Rightarrow {{\text{N}}_{\text{C}}}{\text{ = mg + }}\dfrac{{{\text{m}}{{\text{v}}^{\text{2}}}}}{{{{\text{R}}_{\text{C}}}}}...{\text{(iii)}} \\
$

Since radius of A < radius of C i.e. ${{\text{R}}_{\text{A}}}{\text{ < }}{{\text{R}}_{\text{C}}}$ (from the given figure)
From (i), (ii) and (iii) we get
${{\text{N}}_{\text{A}}}$ is maximum.
Thus, the normal reaction of the road on the body is maximum at A.

Therefore, option (A) is the correct choice.

Note: Action and reaction are equal in magnitude, opposite in direction and the most important point is that both the forces i.e. (action and reaction) act on different bodies not on the same body.