




Concepts of Current Electricity and Magnetism for JEE Advanced Physics
When it comes to JEE Advanced exams, there is no chapter which can be ignored. Just like most of the chapters electricity and magnetism plays a vital role in scoring good grades and ranking. Because of its vast syllabus and concepts, electricity and magnetism are considered one of the most important chapters for JEE advanced exams.
The electricity and magnetism chapter consists of many sub-topics that are considered to be very basic and important. The first concept that we get to see in electricity and magnetism notes is electrostatics. The unit electrostatics and charges is a fundamental part of current electricity and magnetism. In this chapter, we study the link between electricity and magnetism.
The key concepts of the electricity and magnetism chapter are electrostatics, current electricity and the laws related to it, capacitance, magnetostatics, electromagnetic induction, etc.
In this article, we will discuss the electricity and magnetism chapter and the important concepts of the chapter for JEE exam. Let’s start!
JEE Advanced Physics Chapters 2026
Important Topics of Electricity and Magnetism Chapter
Coulomb's law
Gauss law
Electric potential and capacitance
Ohm’s law
Kirchoff’s current and voltage law
Wheatstone Networks
Biot-Savart’s law
Ampere’s law
Electromagnetic induction
Faraday’s law and Lenz law
LC, RC and LCR circuits
LCR series and parallel connections
Electricity and Magnetism Important Concept of JEE Advanced
List of Important Formulas for Electricity and Magnetism Chapter
JEE Advanced Electricity and Magnetism Solved Examples
1. A particle of mass m and charge q moves with a constant velocity v along the positive x direction. It enters a region containing a uniform magnetic field B directed along the negative z direction, extending from x = 3 to x = 5. The minimum value of v required so that the particle can just enter the region.
Sol:
Given,
The mass of the particle=m
Charge of the particle=q
The particle is moving along positive x axis with constant velocity v directed along the negative z axis. Now, we are asked to determine the minimum value of v, for entering the field B.
In this problem, the magnetic field B is perpendicular to the motion of particle the particle in the given region.
Therefore,
The magnetic force=The centripetal force
$qv B=\dfrac {m{v^2}}{r}$
$v=\dfrac {qBr}{m}$
Here, the region is extended from x=3 to x=5, thus the value of r will be:
r=5-3=2
Thus, we get:
$v=\dfrac {2qB}{m}$
Hence, the minimum value of v, for entering the field B is $\dfrac {2qB}{m}$.
Key Point: In this problem we can note one important formula i.e., the minimum value of v when B is perpendicular to the motion of the particle will be $\dfrac {\left({x_2}-{x_3}\right)qB}{m}$.
2. A small circular loop of conducting wire has radius a and carries current I. It is placed in a uniform magnetic field B perpendicular to its plane such that when rotated slightly about its diameter and released, it starts performing simple harmonic motion of time period T. If the mass of the loop is m then :
$T=\sqrt {\dfrac {2m}{IB}}$
$T=\sqrt {\dfrac {\pi m}{IB}}$
$T=\sqrt {\dfrac {\pi m}{2IB}}$
$T=\sqrt {\dfrac {2\pi m}{IB}}$
Sol:
Given that, we have a loop of mass m and radius a, carrying a current I. The current loop is placed in field perpendicular to the magnetic field B.
Now, let us assume that the loop is slightly rotated by an angle $\theta$, then the torque acting on the loop will be:
$\tau = - MB \sin \theta$
$I\alpha=-MB \theta$ (Because, the angle $\theta$ is very small, thus $\sin \theta=\theta$)
$\dfrac {mr^2}{2}\alpha=- \left(\pi {r^2}I\right)B \theta$
$\alpha=\dfrac {2IB\pi}{m}\theta$.....(1)
We know that,
$\alpha = \omega^2 \theta$....(2)
From (1) and (2), we get:
$\omega^2 =\dfrac {2\pi IB}{m}$
$\omega = \sqrt{\dfrac {2\pi IB}{m}}$
Therefore, time period T of rotation will be:
$T=\dfrac {2\pi}{\omega}=\dfrac {2\pi}{\dfrac {2\pi IB}{m}}$
$T=\sqrt {\dfrac {2\pi m}{IB}}$
Therefore, option D is the right answer.
Key Point: To solve the questions like this we need to learn a few standard values of moment of inertia, to save our calculation time.
Previous Year Questions of Electricity and Magnetism
1. A coil having N turns is wound tightly in the form of a spiral with inner and outer radii 'a' and 'b' respectively. Find the magnetic field at centre, when a current I passes through coil: (JEE 2021)
$\dfrac {{\mu_o}IN}{2\left(b-a\right)} \log_e \left(\dfrac {b}{a}\right)$
$\dfrac {{\mu_o}I}{8}\dfrac {a+b}{a-b}$
$\dfrac {{\mu_o}I}{4\left(a-b\right)} \left[\dfrac {1}{a}-\dfrac {1}{b}\right]$
$\dfrac {{\mu_o}I}{8}\dfrac {a-b}{a+b}$
Sol:
Let us consider a small element dr at a distance r. Then the number of turns in the coil will be:
$dN=\dfrac {N}{b-a} dr$
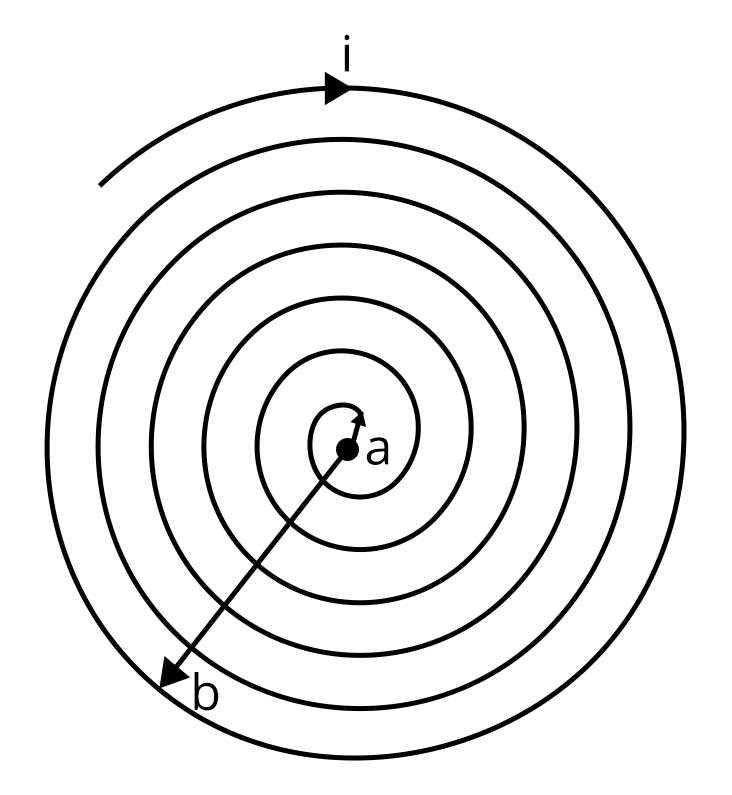
Then the magnetic field due to the element dr at the center of the coil will be:
$dB=\dfrac {{\mu_o}I}{2r} dN$
$dB=\dfrac {{\mu_o}I N}{2 r\left (b-a)\right)}$
$\int_{r=a}^{r=b} dB=\int_{r=a}^{r=b}\dfrac {{\mu_o}I N}{2 r\left (b-a)\right)}$
$B=\dfrac {{\mu_o}I N}{2 \left (b-a)\right)} \log_e \dfrac {b}{a}$
Therefore, option A is the right answer.
Trick: The problem can be easily solved by looking at the the integration part, among all the option, only option A was having logarithmic value.
2. Following plots show magnetization (M) vs magnetizing field (H) and magnetic susceptibility () vs temperature (T) graph : (JEE 2021)
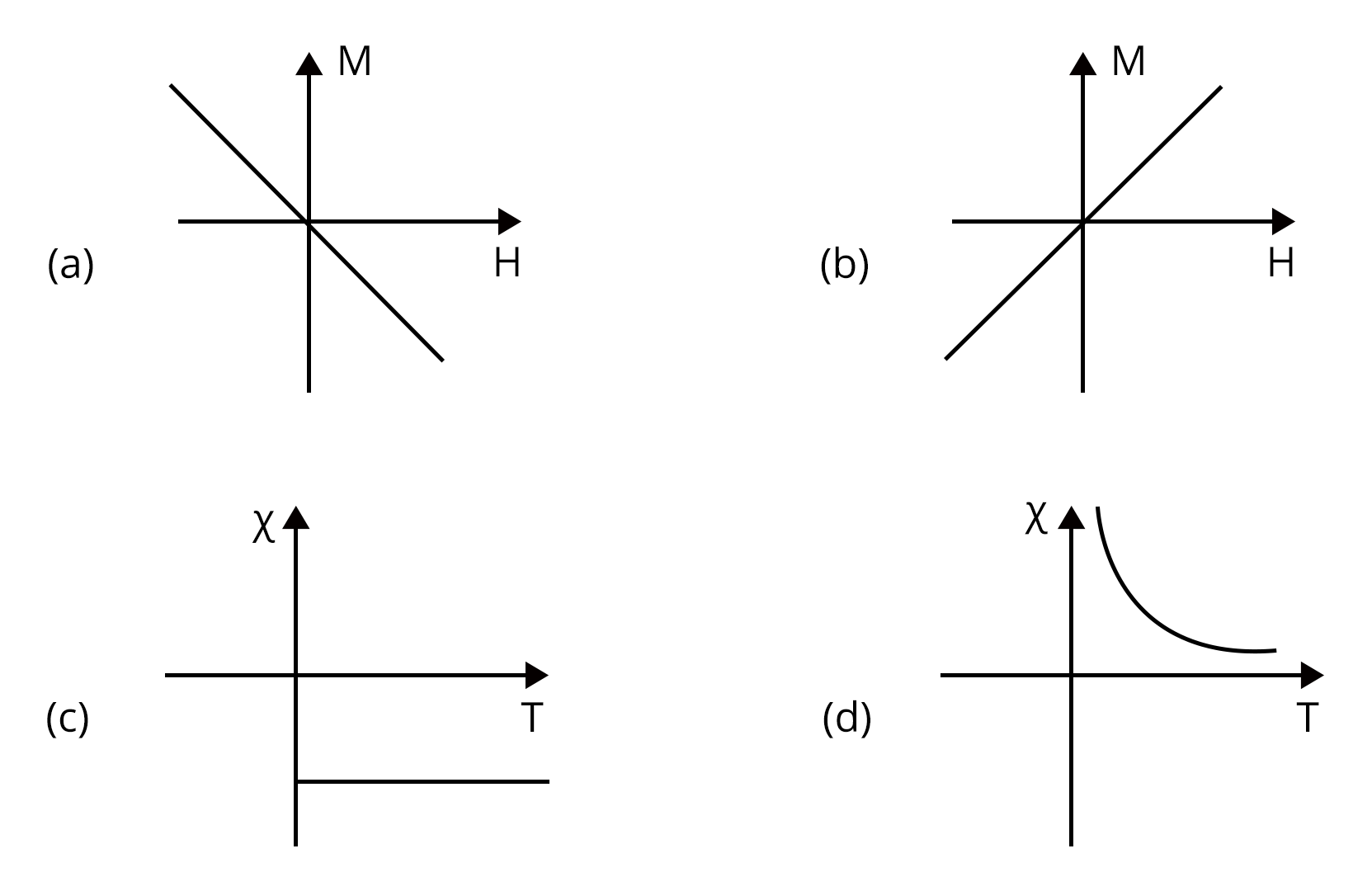
(a), (c)
(a), (d)
(b), (c)
(b), (d)
Which of the following combination will be represented by a diamagnetic material?
Sol:
We know that susceptibility of diamagnetic materials will be negative and independent of temperature. From above graphs, graph (a) and graph (c) represents the diamagnetic material.
Therefore, option a is the right answer.
Trick: From graph eliminate the graphs that are having temperature dependency and porosity susceptibility.
Practice Questions
Electric field of plane electromagnetic wave propagating through a non-magnetic medium is given by E = 20cos(2 1010 t-200x) V/m. The dielectric constant of the medium is equal to : (Take $\mu_r$ = 1) (Ans: 9)
A current of 1.5 A is flowing through a triangle, of side 9 cm each. The magnetic field at the centroid of the triangle is (Assume that the current is flowing in the clockwise direction.) (Ans: $3\times {10^{-5}}$ T, inside the plane of triangle)
JEE Advanced Physics Electricity and Magnetism Study Materials
Here, you'll find a comprehensive collection of study resources for Electricity and Magnetism designed to help you excel in your JEE Advanced preparation. These materials cover various topics, providing you with a range of valuable content to support your studies. Simply click on the links below to access the study materials of Electricity and Magnetism and enhance your preparation for this challenging exam.
JEE Advanced Physics Study and Practice Materials
Explore an array of resources in the JEE Advanced Physics Study and Practice Materials section. Our practice materials offer a wide variety of questions, comprehensive solutions, and a realistic test experience to elevate your preparation for the JEE Advanced exam. These tools are indispensable for self-assessment, boosting confidence, and refining problem-solving abilities, guaranteeing your readiness for the test. Explore the links below to enrich your Physics preparation.
Conclusion
The chapter on Electricity and Magnetism stands as a cornerstone in the realm of physics for JEE Advanced aspirants. It delves into the intricate principles governing electric and magnetic fields, laying the foundation for understanding the complexities of electromagnetism. This chapter's profound knowledge is not only crucial for excelling in the exam but also for mastering advanced concepts in physics and engineering. Students who grasp the intricacies of electric and magnetic fields gain the ability to solve intricate problems, analyze real-world applications, and pave the way for innovations in technology. It's a chapter that empowers future scientists and engineers to unlock the mysteries of the physical world.
FAQs on Electricity and Magnetism - Physics JEE Advanced
1. Is electricity and magnetism important for JEE?
In terms of complexity and weightage, 'Electricity and Magnetism' is one of the most important topics in the JEE syllabus. You can be confident of a high overall score if you have a firm grasp on this subject.
2. What is the weightage of electricity and magnetism in JEE Mains?
Due to its vast syllabus electricity and magnetism bagged high weightage in exam. Nearly 5-6 questions have been asked repeatedly which carry about 15-20 marks.
3. Is electricity and magnetism chapters tough?
No, both the chapters are interrelated to each other. Hence if we prepare thoroughly for electricity part, we can easily understand magnetism concepts. So these are not tough chapters.
4. Who unified electricity and magnetism?
Unification of electricity and magnetism credit goes to physicist James Clerk Maxwell.























