JEE Important Chapter - Integral Calculus

The branch of calculus where we examine integrals and their properties is known as integral calculus. Integration is a crucial concept because it is the inverse of differentiation. The fundamental theorem of calculus connects integral and differential calculus. 

In this article, we will go over integral calculus in detail, including why it's employed, its types, formulas, examples, and applications. Also, for a better understanding and knowledge, we will go over some of the solved problems and previous year's questions.

JEE Main Maths Chapter-wise Solutions 2025 

Important Topics of Integral Calculus

• Indefinite integral

• Properties of indefinite integral

• Methods of integration

• Integration by substitution

• Integration using trigonometric functions

• Integration by partial fractions

• Integration by parts

• Integrals of some particular function

• Integral of some special types

• Definite integral and its properties

• The fundamental theorem of calculus

• Evaluations of definite integral by substitution

Important Topics of Integral Calculus

What is Integral Calculus?

The values of the function discovered through the integration process are known as integrals. Integration is the process of obtaining f(x) from f'(x). Integrals assign numbers to functions in a way that represents displacement and motion problems, area and volume problems, and other problems that arise when little data is combined. We can find the function f by using the derivative f' of the function f and that function f is referred to as antiderivative or integral of f' in this case.

Types of Integrals

Integral calculus is used to solve problems of the following types given below:

A. The first type of problem is to find the function if its derivative is given.

B.  Also, the problem is related to finding the area bounded by the graph of a function under given conditions. Further,  the Integral calculus is divided into two types.

• Definite Integrals (in which the value of the integrals are definite)

• Indefinite Integrals (in which the value of the integral is indefinite with an arbitrary constant, C)

Indefinite Integrals

The integrals which do not have a pre-existing value of limits, which makes the final value of integral indefinite, I.e, ∫g'(x)dx = g(x) + c. Indefinite integrals are part of the family parallel curves.

Definite Integrals

Definite integral is one that has a pre-existing value of limits, which makes the final value of the integral, definite. if  a function of the curve is f(x) , then $\int\limits_a^b f(x) dx = f(b) - f(a)$

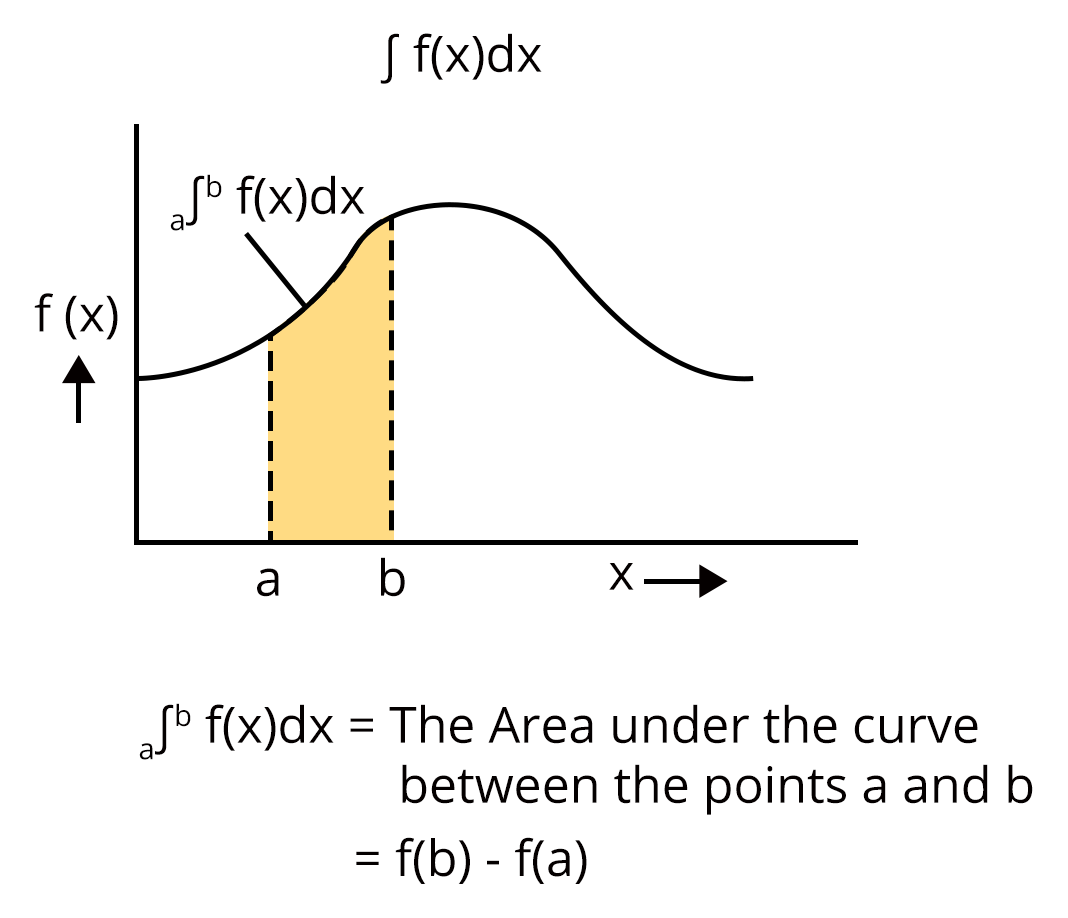
Image: Definite Integral

Fundamental Theorems of Integral Calculus

Integrals are defined as the function of the area bounded by the curve y = f(x), a ≤ x ≤ b, at X-axis where the ordinates are x = a and x =b, and b>a. Let x be a given point in $[$a,b$]$. Then $\int\limits_a^b f(x) dx$ represents the area function. This concept of area function leads to the fundamental theorems of integral calculus.

• First Fundamental Theorem of Integral Calculus

• Second Fundamental Theorem of Integral Calculus

First Fundamental Theorem of Integrals

A(x) = $\int\limits_a^b f(x) dx$ for all x ≥ a, where the function is continuous on $[$a,b$]$. Then A'(x) = f(x) for all x ϵ $[$a,b$]$

Second Fundamental Theorem of Integrals

If f is continuous function of x defined on the closed interval $[$a,b$]$ and F is another function such that d/dx F(x) = f(x) for all x in the domain of f, then $\int\limits_a^b f(x) dx$ = f(b) -f(a). This is known as the definite integral of f over the range $[$a,b$]$, Where a is the lower limit and b is the upper limit. 

Properties of Integral Calculus

Let us go through some of the properties of the indefinite integrals:

• The derivative of an integral is the integrand of itself, ∫ f(x) dx = f(x) +C.

• Since two indefinite integrals with the same derivative produce the same family of curves, they are equivalent, ∫ $[$ f(x) dx - g(x) dx$]$ = 0.

• The sum or the difference of a finite number of functions is equal to the sum or difference of the individual functions' integrals, ∫ $[$ f(x) dx+g(x) dx$]$ = ∫ f(x) dx + ∫ g(x) dx.

• The constant is taken outside the integral sign, ∫ k f(x) dx = k ∫ f(x) dx, where k ∈ R.

• The previous two properties are combined to get the form: ∫ $[k_1 f_1(x)$ + $k_2 f_2(x)$ +... $k_n f_n(x)]\; dx$ = $k_1 \lim f_1(x)\;dx$ + $k_2 \lim f_2(x)\;dx$+ ... $k_n \lim f_n(x)\;dx$

Methods of Finding Integrals of Functions

We have different methods to find the integral of a given function in integral calculus. Some of the most commonly used methods of integration are:

• Integration by Parts

• Integration using Substitution

• Integration by Partial Fractions

Uses of Integral Calculus

Integral Calculus is mainly used for the two purposes mentioned below:

• To calculate f from f’: If a function f is differentiable in the interval of consideration, then f’ is defined. We've already seen how to calculate a function's derivatives in differential calculus, and we can "undo" that with the help of integral calculus.

• To find the area under a curve.

Application of Integral Calculus

Some of the important applications of the integral calculus are - Integration is applied to find:

• The area between two curves

• Centre of mass

• Kinetic energy

• Surface area

• Work

• Distance, velocity and acceleration

• The average value of a function

• Volume

List of Integral Calculus Formulae

Solved Integration Examples 

Example 1: Find the integral of the function f(x) = $\sqrt{x}$.

Solution:

Given,

f(x) = $\sqrt{x}$

∫f(x) dx = $\int \sqrt{x} dx$

$\begin{array}{l}\int \sqrt{x}\ dx = \int x^{\frac{1}{2}}\ dx\end{array} $

We know that, $\begin{array}{l}\int x^{n}\ dx = \frac{x^{n+1}}{n+1}+C\end{array} $

Now, $\begin{array}{l}\int \sqrt{x}\ dx = \frac{x^{\frac{1}{2}+1}}{\frac{1}{2}+1}+C\\= \frac{x^{\frac{1+2}{2}}}{\frac{1+2}{2}}+C\\=\frac{2}{3}x^{\frac{3}{2}}+C\end{array} $

Example 2: Find the integral of cos2n with respect to n.

Solution:

Let f(n) = cos2n 

we know that 2 cos2A = cos 2A + 1

So, f(n) = (1/2)(cos 2n + 1)

Let us find the integral of f(n).

∫f(n) dn = ∫(1/2)(cos 2n + 1) dn

= (1/2) ∫(cos 2n + 1) dn

= (1/2) ∫cos 2n dn + (1/2)∫1 dn

= (1/2) (sin 2n/2) + (1/2) n + C

= (sin 2n/4) + (n/4) + C

=(1/4)$[$sin 2n + n$]$ + C

Solved Previous year Questions 

Question 1: ∫{$[$sin8x − cos8x$]$ / $[$1 − 2 sin2x cos2x$]$} dx = _________.

Solution:

∫{$[$sin8x − cos8x$]$ / $[$1 − 2 sin2x cos2x$]$} dx

= ∫{$[$(sin4x + cos4x) * (sin4x − cos4x)$]$ / $[$(sin2x + cos2x)2 − 2 sin2x cos2x$]$} dx

= ∫(sin4x – cos4x) dx

= ∫$[$sin2x + cos2x$] \times [$sin2x – cos2x$]$ dx

= ∫(sin2x - cos2x) dx

= ∫−cos2x dx

= $[$−sin2x/2$]$ + c

Question 2: ∫x2dx / (a + bx)2 = ___________.

Solution:

$ \int \frac{x^{2}}{(a+b x)^{2}} d x $

Let $ a+b x=t \Rightarrow b\; d x=d t $

$ s_{0}, \frac{1}{b} \int \left(\frac{t-a}{b t}\right)^{2} d t=\frac{1}{b^{3}} \int\left(1-\frac{a}{t}\right)^{2} d t $

$ =\frac{1}{b^{3}} \int\left(1+\frac{a^{2}}{t^{2}}-\frac{2 a}{t}\right) d t $

$=\frac{1}{b^3}\left [ \int dt +a^2\int\frac{dt}{t^2}-2a\int \frac{dt}{t}\right ]$

$ =\frac{1}{b^{3}}\left[ t+a^{2} \left( -\frac{1}{t} \right) -2 a\; ln\; t \right]+c $

$ =\frac{a+b x}{b^{3}}-\frac{a^{2}}{b^{3}(a+b x)}-\frac{2 a}{b^{3}} ln (a+bx)+c $

$ =\frac{x}{b^{2}}-\frac{a^{2}}{b^{3}(a+b x)}-\frac{2 a}{b^{3}} ln (a+bx)+k $

Question 3: $\int \left [ {x^5}/{\sqrt{1+x^3}} \right ] dx$ = ________.

Solution:

Put 1 + x3 = t2

⇒ 3x2 dx = 2tdt and x3 = t2 − 1

So, ∫$x^5 /\sqrt{1+x^3} \; dx$ = ∫{$[x^2$ $\times$ $x^3]$ / $\sqrt{1+x^3} \; dx$

= $\left [ \dfrac{2}{3} \right ]$ ∫{$[$(t2 − 1) $\times$ t$]$ dt / $[$t$]$}

= $\left [ \dfrac{2}{3} \right ]$ ∫(t2 − 1) dt

= $\left [ \dfrac{2}{3} \right ]$ $[$(t3 / 3) − t$]$ + c

= $\left [ \dfrac{2}{3} \right ]$ $[${(1 + x3)3/2 / 3} − {(1 + x3)½}$]$+ c

Practise Problems 

1. Let p(x) be a function defined on R such that p'(x) = p'(1 – x), for all x $\in$0, 1], p(0) = 1 and p(1) = 41. Then $\int_{0}^{1}$ p(x) dx equals:

(A) $\sqrt{41}$ 

(B) 21 

(C) 41 

(D) 42

2. The value of $\int_{0}^{1} \frac{8 \log (1+x)}{1+x^{2}} d x$ is:

(A) $\frac{\pi}{2} \log 2$

(B) $\log 2$

(C) $\pi \log 2$

(D) $\frac{\pi}{8} \log 2$

Answers: 1. (B), 2. (C)

Conclusion 

Integral calculus is an extremely important concept to learn. Integral calculus is a branch of calculus that includes differential calculus and is utilised in physics. Aspirants preparing for the JEE Main exam can use this article to learn the fundamentals of integrals such as definition, types of integrals, and properties. They can also look at the solved examples and previous year's problems to gain a better understanding and knowledge.

Study Materials for Integral Calculus:

These study materials will aid you in comprehending Integral Calculus, ensuring a solid foundation for further mathematical pursuits.

Important Links for JEE Main and Advanced 2025

Access a curated collection of study materials and tips to excel in JEE Main and Advanced 2025, helping you prepare effectively for these prestigious engineering entrance exams.