




Introduction of Trigonometry
Trigonometry is a branch of mathematics that studies the relationship between the sides and angles of a right-angled triangle. It is one of the most important branches in the history of mathematics. Hipparchus, a Greek mathematician, introduced this concept. We will learn the fundamentals of trigonometry in this article, including trigonometry functions, ratios, the trigonometry table, formulas, and many solved examples.
JEE Main Maths Chapter-wise Solutions 2026
JEE Main Maths Chapter-wise Solutions | |||
1 | 9 | ||
2 | 10 | ||
3 | 11 | ||
4 | 12 | ||
5 | 13 | ||
6 | 14 | ||
7 | 15 | Trigonometry | |
8 | 16 | ||
Important Topics of Trigonometry
Trigonometric Ratios
Trigonometry - Formulas, Identities, Functions and Problems
Important Trigonometry Concepts
What is Trigonometry?
The word Trigonometry is clubbed as, 'Trigonon' which means triangle and 'Metron' means to measure. The branch of mathematics known as "trigonometry" studies the relationship between the sides and angles of a right-angle triangle. Using trigonometric formulas, functions, or identities, it is possible to find the missing or unknown angles or sides of a right triangle. The angles in trigonometry can be measured in degrees or radians. 0°, 30°, 45°, 60°, and 90° are some of the most commonly used trigonometric angles in calculations.
Trigonometry is further divided into two subcategories. The following are the two types of trigonometry:
Plane Trigonometry and Spherical trigonometry
Basic Trigonometry
The measurement of angles and problems involving angles are covered in the fundamentals of trigonometry. Trigonometry has three basic functions: sine, cosine, and tangent. Other important trigonometric functions can be derived using these three basic ratios or functions: cotangent, secant, and cosecant. These functions are the foundation for all of the important concepts in trigonometry.
Ratios in trigonometry: Sine, Cosine, and Tangent
The trigonometric functions are the trigonometric ratios of a triangle. The trigonometric functions sine, cosine, and tangent are abbreviated as sin, cos, and tan. Let's look at how these ratios or functions are evaluated in a right-angled triangle.
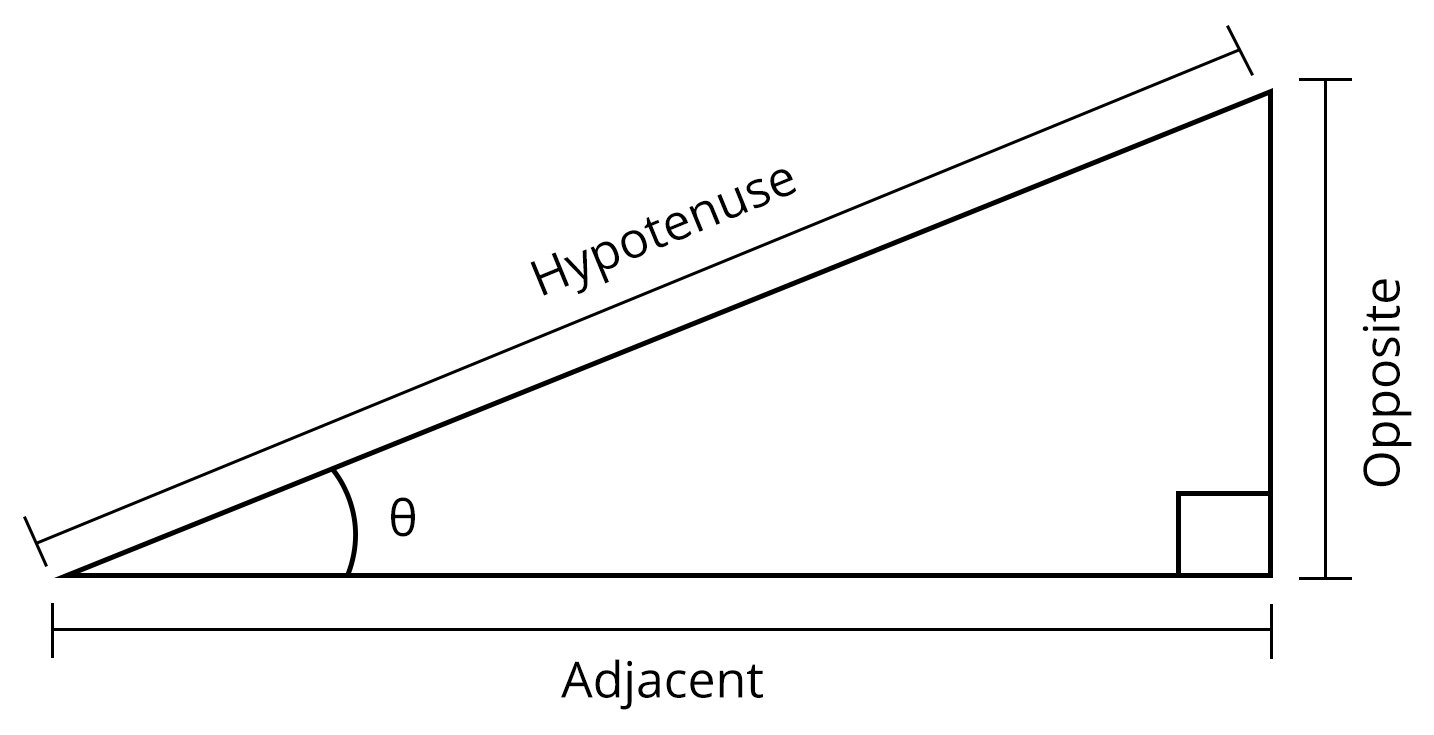
Consider a right-angled triangle with the longest side being the hypotenuse and the sides opposite to the hypotenuse being the adjacent and opposite sides.
Trigonometric Functions Formula
If is the angle formed by the base and hypotenuse in a right-angled triangle, then
The values of the other three functions, cot, sec, and cosec, are determined by the values of tan, cos, and sin.
Even and Odd Trigonometric Functions
Even or odd can be used to describe the trigonometric function.
Odd Trigonometric Functions: If f(-x) = -f(x) and symmetric with respect to the origin, a trigonometric function is said to be odd.
Even Trigonometric Functions: If f(-x) = f(x) and symmetric to the y-axis, a trigonometric function is said to be even.
Trigonometric Functions in Different Quadrants
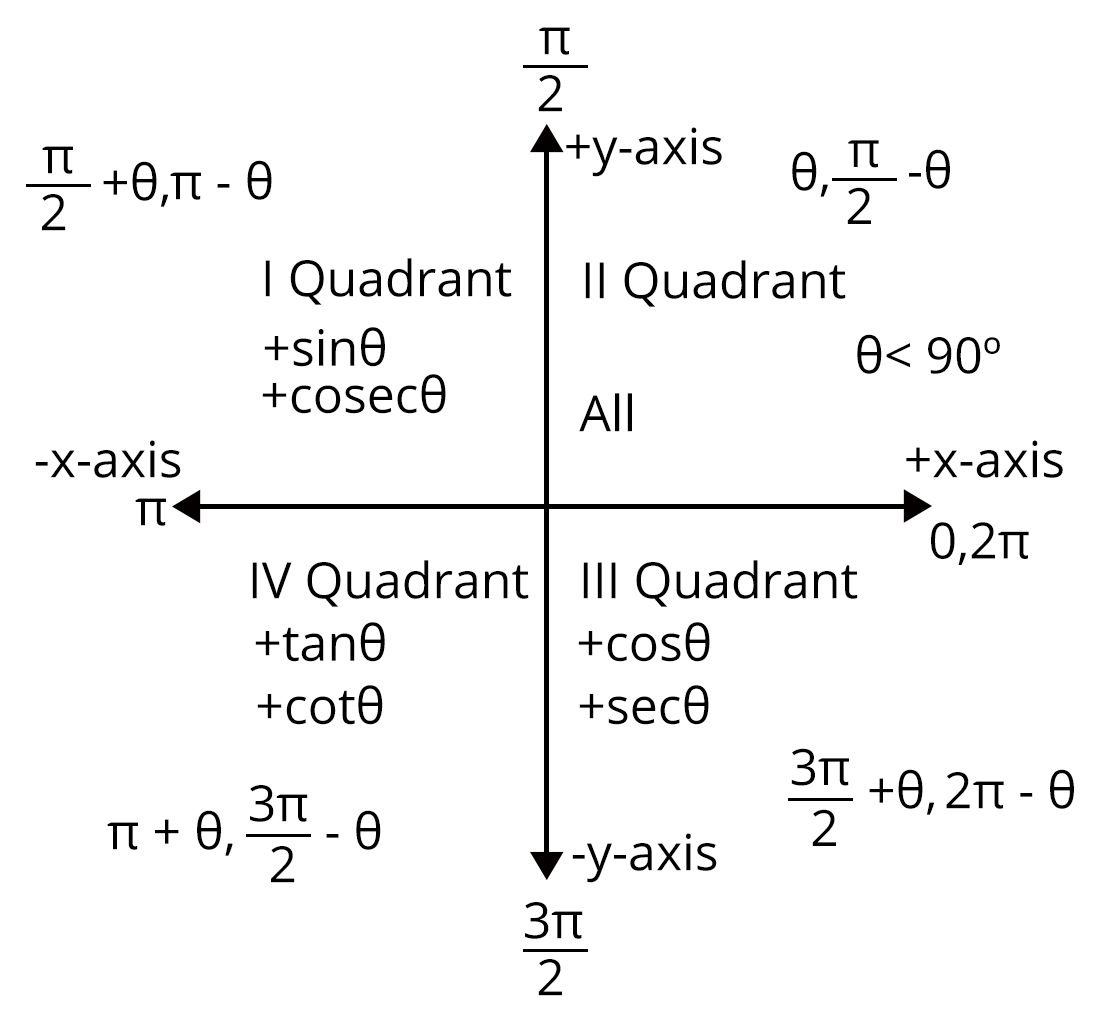
I Quadrant | II Quadrant |
increases from 0 to 1 | decreases from 1 to 0 |
decreases from 1 to 0 | decreases from 0 to -1 |
increases from 0 to | increases from to 0 |
decreases from to 0 | decreases from 0 to |
increases from 1 to | increases from to -1 |
decreases from to 1 | decreases from 1 to |
III Quadrant | IV Quadrant |
increases from 0 to -1 | increases from -1 to 0 |
decreases from -1 to 0 | increases from 0 to 1 |
increases from 0 to | increases from to 0 |
decreases from to 0 | decreases from 0 to |
decreases from -1 to | decreases from to 1 |
decreases from to -1 | decreases from -1 to |
Trigonometric Table - Trigonometry Table Formula
The trigonometric table is made up of interrelated trigonometric ratios such as sine, cosine, tangent, cosecant, secant, and cotangent are used to calculate standard angle values. Refer to the below trigonometric table chart to know more about these ratios.
Angles | |||||
0 | 1 | ||||
1 | 0 | ||||
0 | 1 | ||||
1 | |||||
1 | 2 | ||||
1 | 0 |
Similarly, we can find the trigonometric ratio values for angles other than 90 degrees, such as 180 degrees, 270 degrees, and 360 degrees.
Important Trigonometric Angles
Trigonometric angles are the angles in a right-angled triangle that can be used to represent various trigonometric functions. and are some of the standard angles used in trigonometry. These angles' trigonometric values can be found directly in a trigonometric table. and are some other important angles in trigonometry. The angle of trigonometry can be expressed in terms of trigonometric ratios as follows:
Unit Circle
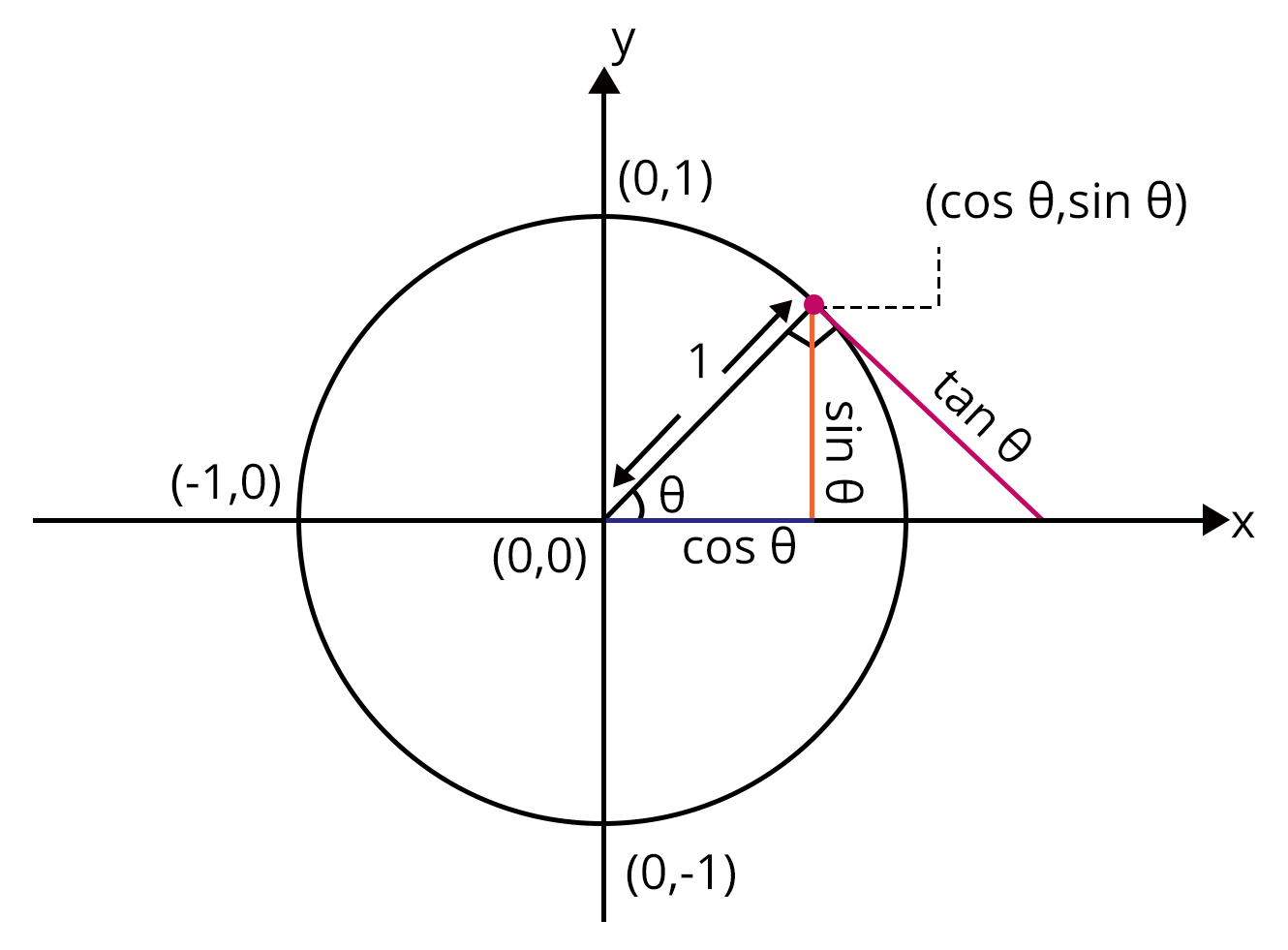
Because the center of the circle is at the origin and the radius is 1, the concept of unit circle allows us to directly measure the angles of cos, sin, and tan. Assume theta is an angle, and the length of the perpendicular is y and the length of the base is x. The hypotenuse is the same length as the radius of the unit circle, which is 1. As a result, the trigonometry ratios can be written as;
List of Trigonometric Formulas
There are different formulas in trigonometry depicting the relationships between trigonometric ratios and the angles for different quadrants. The basic trigonometry formulas list is given below:
1. Pythagorean Identities
2. Sine and Cosine Law in Trigonometry
Sine Law:
Cosine Law:
The lengths of the triangle's sides are a, b, and c, and the triangle's angle is A, B, and C.
3. Sum and Difference identities
Let u and v be the angles:
4. Trigonometry Identities
5. Euler's Formula for trigonometry
Where is the angle and is the imaginary number.
Hence Euler’s formula for and is:
Trigonometry notes on Trigonometry Identities
The trigonometry identities are the trigonometry equations that include all of the trigonometry ratios of all the angles
Each trigonometric ratio can be expressed in terms of another trigonometric ratio.
We can easily find the other value of the trigonometry ratio if we know one of the values of the trigonometry ratio.
They can also be used to calculate trigonometric formulas.
Application of Trigonometry
The height of a structure or a mountain is calculated using trigonometry. The height of a building can be easily calculated using trigonometric functions and the distance of a structure from the perspective. It is used in a variety of fields and has no specific applications in solving functional problems. For example, in the development of computer music, trigonometry is used: as you may know, sound travels in waves, and this wave pattern is used in the development of computer music by passing it through a sine or cosine function.
Trigonometry Examples:
Example 1: A man stands in front of a 44 foot pole. According to his calculations, the pole cast a shadow that was 13 feet long. Can you assist him in determining the sun's angle of elevation from the shadow's tip?
Ans: Let x be the angle of elevation of the sun,
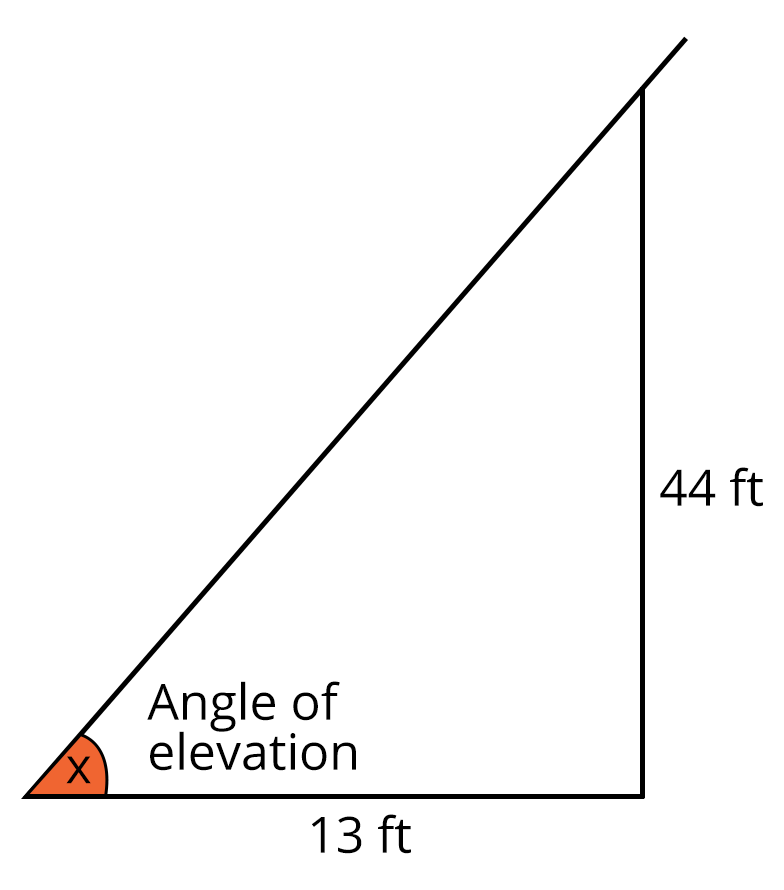
Hence, in degree is
Example 2: Find the value of
Ans: Given,
To find the value of use the formula
Split such that and
Solved problems of Previous Year Question
1. Find the general solution of is _________.
Ans:
2. Find the value of ?
Ans: Let
Hence,
W.K.T
W.K.T
3. A balloon is observed simultaneously from three points A, B and C on a straight road directly under it. The angular elevation at B is twice and at C is thrice that of A. If the distance between A and B is 200 meters and the distance between B and C is 100 meters, then the height of the balloon is given by _________.
Ans:
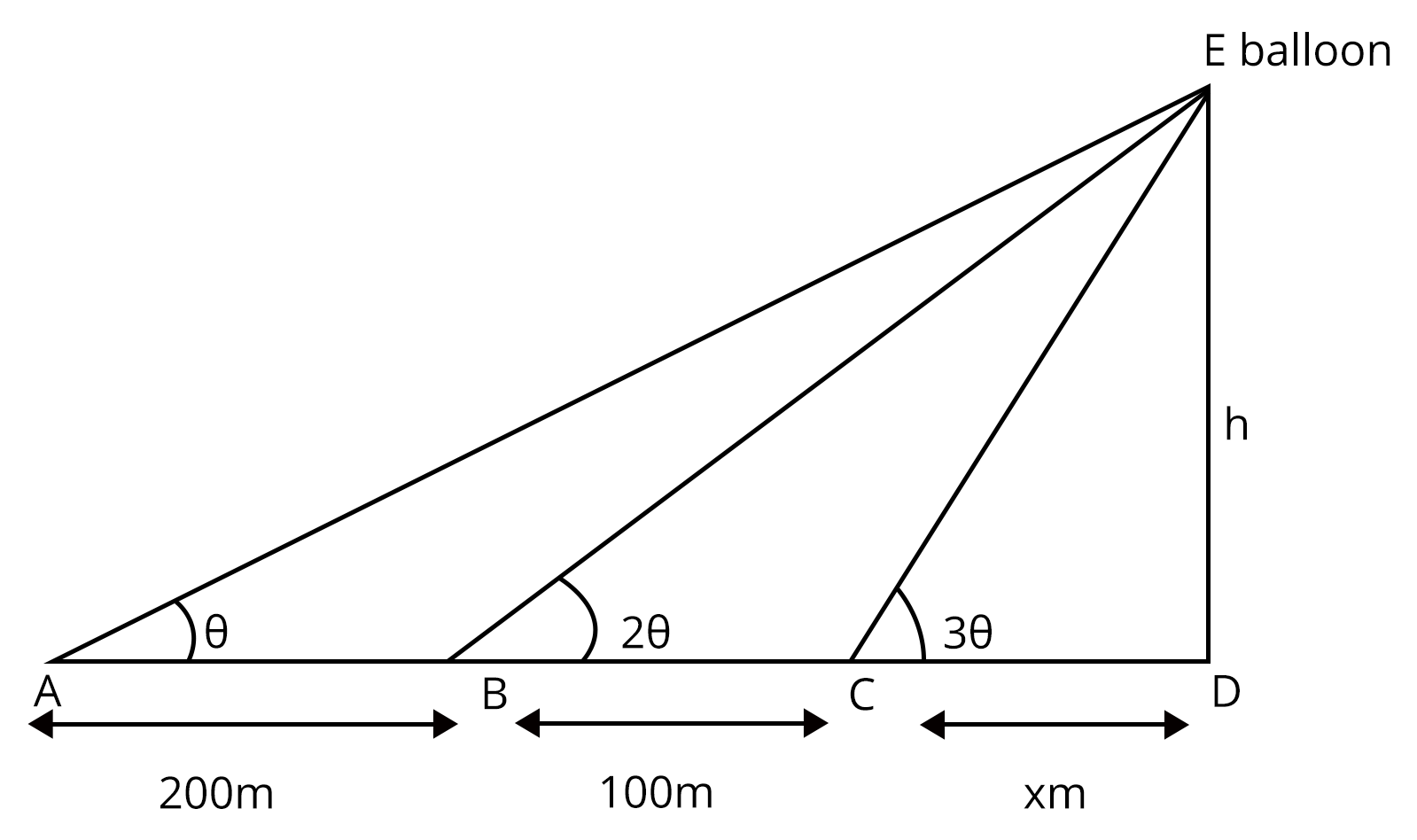
—(i)
—(ii)
—(iii)
From (i) and (ii), we get
On simplifying we get,
—(iv)
Similarly,
From (ii) and (iii), we get
On simplifying we get,
—(v)
Now divide equation (iv) and (v) we get,
—(vi)
W.K.T
So, From equation (vi) we get,
or
Hence
So the height of the balloon is
Practice problems
1. Find the value of _________.
Ans: 15
2. If then ________.
Ans: 1
Conclusion
Although trigonometry does not have many practical applications, it does make it easier to work with triangles. It's an excellent addition to geometry and actual measurements. With trigonometry, you can easily find the height without actually climbing a tree. They have a wide range of applications in real life and are extremely useful to most architects and astronomers. A standard trigonometry table helps solve subject-related problems. The 3 basic measures are sin, cos, and tan, and the remaining three are calculated using the formula given in the above list of formulas.
Study Materials for Trigonometry:
These study materials will aid you in comprehending Trigonometry, ensuring a solid foundation for further mathematical pursuits.
Important Links for JEE Main and Advanced 2026
Access a curated collection of study materials and tips to excel in JEE Main and Advanced 2026, helping you prepare effectively for these prestigious engineering entrance exams.
FAQs on JEE Important Chapter - Trigonometry
1. Who is the founder of trigonometry?
A Greek astronomer, geographer and mathematician, Hipparchus discovered the concept of trigonometry.
2. What Does $\theta$ Mean in Trigonometry?
In trigonometry, $\theta$ is used to represent a measured angle as a variable. It's the angle formed by the horizontal plane and the line of sight from the observer's eye to a higher object. Depending on the object's position, it's called the angle of elevation or the angle of depression. When the object is above the horizontal line, it's called the angle of elevation, and when it's below the horizontal line, it's called the angle of depression.
3. What is the best way to find trigonometric functions?
The ratio of the sides of a right-angled triangle is the trigonometric function. The Pythagorean rule Hypotenuse2 = Altitude2 + Base2 is also applied. In addition, the trigonometric functions have different values for different angles between the hypotenuse and the right triangle's base.























