JEE Advanced 2023 Revision Notes for Algebra

Complex Number

A complex number is one that has the form $z = x + iy$, where $x,y \in R$ and $i = \sqrt { - 1} $and where $x$ is the real part and $y$ is the imaginary part, and it is expressed as $\operatorname{Re} (z) = x,\operatorname{lm} (z) = y$. If $x = 0$, the complex number is purely imaginary, and if $y = 0,$ it is purely real.

A complex number is also defined as an ordered pair of real numbers, and it is represented by the symbol $(a,b)$. If we write $z = (a,b)$ the real part is $a$ and the imaginary part is $b$ of the complex number $z.$

Imaginary Numbers 

Real numbers multiplied by the imaginary unit I yield imaginary numbers. In mathematics, the letter i (or 'j' in some books) represents the imaginary part of any complex number. It allows us to distinguish between any complex number's real and imaginary parts. Furthermore, it is not only not distinguishable but also has some value. 

${\mathbf{i}}{\text{ }} = {\text{ }}\sqrt { - 1}$

Algebra of complex numbers

Complex Number Equality 

Two Complex numbers ${z_1}$ and ${z_2}$ are equal if,

Condition 1) $\operatorname{Re} \left( {{z_1}} \right) = \operatorname{Re} \left( {{z_2}} \right)$

Condition 2) $\operatorname{Im} \left( {{z_1}} \right) = \operatorname{Im} \left( {{z_2}} \right)$

So, if, ${z_1} = x + 3i$ and ${z_2} =  - 2 + {y_i}$ are equal, then according to the above conditions, 

$\operatorname{Re} \left( {{z_1}} \right) = x$ and $\operatorname{Re} \left( {{z_2}} \right) =  - 2$, so $x =  - 2$

And Similarly

$\operatorname{Im} \left( {{z_1}} \right) = 3{\text{ and }}\operatorname{Im} \left( {{z_2}} \right) = y{\text{, so }}y = 3$

Algebraic Operations with Complex Numbers

• Addition: $(a + ib) + (c + id) = (a + c) + i(b + d)$

• Subtraction:$(a + ib) - (c + id) = (a - c) + i(b - d)$

• Multiplication : $(a + ib)(c + id) = ac + iad + ibc + {i^2}bd = (ac - bd) + i(ad + bc)$

• Division : $\dfrac{{a + ib}}{{c + id}}{\text{ }} = \dfrac{{(a + ib)(c - id)}}{{(c + id)(c - id)}}$$ = \dfrac{{(ac + bd)}}{{{c^2} + {d^2}}} + i\dfrac{{(bc - ad)}}{{{c^2} + {d^2}}}$

Addition of Complex Numbers

If ${z_1} = a + ib$ and ${z_2} = c + id$, then the sum of these two complex numbers, ${z_1} + {z_2}$, is calculated as: 

${z_1} + {z_2} = (a + ib) + (c + id) = (a + c) + i(b + d)$

Therefore,

${z_1} + {z_2} = \operatorname{Re} \left( {{z_1} + \operatorname{Re}{z_2}} \right) + \operatorname{Im} \left( {{z_1} + {z_2}} \right)$

Addition of complex numbers can be another complex number.

Addition of complex numbers satisfies the following properties

• Closure Law: That is, the sum of two complex numbers is another complex number. If ${z_1} + {z_2}$ where ${z_1}$ and ${z_2}$ are complex numbers, then $z$ will be a complex number as well. 

• Commutative Law: According to commutative law, for any two complex numbers ${z_1}$ and ${z_2},{z_1} + {z_2} = {z_2} + {z_1}$.

• Associative Law: For any three complex numbers say $\left( {{z_1} + {z_2}} \right) + {z_3} = {z_1} + \left( {{z_2} + {z_3}} \right)$.

• Existence of Additive Identity:  Additive identity, also known as zero complex number, is denoted by 0 (or $0 + i0$), which means that for any complex number $z,z + 0 = z$. 

• Existence of Additive Inverse:  The additive inverse or negative of any complex number z is a complex number with the opposite sign in both its real and imaginary parts.

It is symbolised by $ - z$ and $z + ( - z) = 0$. 

Difference of Two Complex Numbers

If ${z_1} = a + ib$ and ${z_2} = c + id$ the difference of these two complex numbers is ${z_1} - {z_2}$ is calculated as follows: 

${z_1} - {z_2} = (a + ib) - (c + id){\text{ }}$

$ = (a - c) + i(b - d)$

Therefore,

${z_1} - {z_2} =\operatorname{Re}\left( {{Z}_{1}} \right)+\operatorname{Re}\left( {{Z}_{2}} \right) + \operatorname{Im} \left( {{z_1} - {z_2}} \right)$

A complex number's difference can be another complex number. 

Multiplication of Two Complex Numbers

If $z_{1}=a+i b \text { and } z_{2}=c+i d$ then the product of these two complex numbers is.

${z_1} \times {z_2}$ is calculated as follows: 

${z_1} \times {z_2} = (a + ib) \times (c + id){\text{ }}$

${{z}_{1}}{{z}_{2}}~=\text{ }ac\text{ }+\text{ }i\left( ad \right)\text{ }+\text{ }i\left( bc \right)\text{ }+\text{ }{{i}^{2}}\left( bd \right)$

${{z}_{1}}{{z}_{2}}~=\text{ }ac\text{ }+\text{ }i\left( ad \right)\text{ }+\text{ }i\left( bc \right)\text{ }+\text{ }\left( -1 \right)\left( bd \right)$

${z_1} \times {z_2} = (ac - bd) + i(ad + bc)$

Therefore,

${z_1} \times {z_2} = \left[ {\operatorname{Re} \left( {{z_1}} \right)\operatorname{Re} \left( {{z_2}} \right) - \operatorname{Im} \left( {{z_1}} \right)\operatorname{Im} \left( {{z_2}} \right)} \right] + i\left[ {\operatorname{Re} \left( {{z_1}} \right)\operatorname{Im} \left( {{z_2}} \right) + \operatorname{Im} \left( {{z_2}} \right)\operatorname{Re} \left( {{z_2}} \right)} \right]$

Division of Two Complex Numbers

If ${z_1} = a + ib$ and ${z_2} = c + id$then the division of these two complex numbers, $\dfrac{z_1}{z_2}$, is calculated as follows: 

$\dfrac{{{z_1}}}{{{z_2}}} = \dfrac{{(a + ib)}}{{(c + id)}}$

On Rationalization:

$\dfrac{{{z_1}}}{{{z_2}}} = \dfrac{{(a + ib)}}{{(c + id)}} \times \dfrac{{(c - id)}}{{(c - id)}}{\text{ }}$

$\dfrac{{{z_1}}}{{{z_2}}} = \dfrac{{(ac + bd)}}{{\left( {{c^2} + {d^2}} \right)}} + \dfrac{{i(bc - ad)}}{{\left( {{c^2} + {d^2}} \right)}}$

Conjugate of Complex Number

A complex number's conjugate $z = a + ib$ is obtained by changing the sign of the imaginary part of $z$, which is denoted as $\bar z$

$\bar z = a - ib$

$z + \bar z = 2a$

$z - \bar z = 2bi$

Modulus of a Complex Number

The modulus of a complex number is the distance from the origin of the point on the argand plane representing the complex number z.  

Let P be the point corresponding to the complex number $z = x + iy.$

Then $OP = \left| z \right| = \sqrt {({x^{2\;}} + {\text{ }}{y^2}\;)} .$

Modulus Properties 

(i) $|z| = 0 \Leftrightarrow z = 0$

(ii) $|z|=\left| {\bar{z}} \right|=|-z|=\left| -\bar{z} \right|$

(iii) $ - |z| \leqslant \operatorname{Re} (z) \leqslant |z|$

(iv) $ - |z| \leqslant \operatorname{Im} ({\text{z}}) \leqslant |{\text{z}}|$

(v) $z{\bar{z}} = |z{|^2}$

If ${z_1},{z_2}$ are two complex numbers, then

(vi) $\left| {{z_1}{z_2}} \right| = \left| {{z_1}} \right| \cdot \left| {{z_2}} \right|$

(vii) $\left| \dfrac{z_1}{z_2} \right| = \left| \dfrac{z_1}{z_2}\right|$, if ${z_2} \ne 0$

(viii) ${{\left| {{z}_{1}}+{{z}_{2}} \right|}^{2}}={{\left| {{z}_{1}} \right|}^{2}}+{{\left| {{z}_{2}} \right|}^{2}}+{{\bar{z}}_{1}}{{\bar{z}}_{2}}+{{z}_{1}}{{\bar{z}}_{2}}={{\left| {{z}_{1}} \right|}^{2}}+{{\left| {{z}_{2}} \right|}^{2}}+2\operatorname{Re}\left( {{z}_{1}}{{{\bar{z}}}_{2}} \right)$

(ix) ${{\left| {{z}_{1}}+{{z}_{2}} \right|}^{2}}+{{\left| {{z}_{1}} \right|}^{2}}-{{\left| {{z}_{2}} \right|}^{2}}-{{\bar{z}}_{1}}{{\bar{z}}_{2}}-{{z}_{1}}{{\bar{z}}_{2}}={{\left| {{z}_{1}} \right|}^{2}}+{{\left| {{z}_{2}} \right|}^{2}}-2\operatorname{Re}\left( {{z}_{1}}{{{\bar{z}}}_{2}} \right)$

(x) ${\left| {{z_1} + {z_2}} \right|^2} + {\left| {{z_1} - {z_2}} \right|^2} = 2\left( {{{\left| {{z_1}} \right|}^2} + {{\left| {{z_2}} \right|}^2}} \right)$

Modulus and Argument of a Complex Number

Let $z = x + iy = (x,y)$ for all $x,y$ $\in {\text{R}}$ and ${\text{i}} = \sqrt { - 1} $

(Image will be uploaded soon)

Modulus of a Complex Number

The length OP is known as the modulus of the complex number $z$, which is denoted by $\left| z \right|$. 

i.e. ${\text{OP}} = {\text{r}} = |{\text{z}}| = \sqrt {\left( {{x^2} + {y^2}} \right)} $

If $(x,y) \ne (0,0)$ $\theta $ is known as the argument or amplitude of $z$,

i.e. $\theta  = {\tan ^{ - 1}}\left( {\dfrac{y}{x}} \right)$ [angle made by OP with positive $X$-axis]

or $\arg (z) = {\tan ^{ - 1}}\dfrac{y}{x}$

Also, the argument of a complex number is not unique since if  $\theta$ is a value of the argument, so also in $2n\pi \text{ }+\text{ }\theta$

Furthermore, the argument of a complex number is not unique, because if $\theta $ is a value of the argument, then it is also in $2n\pi  + \theta $, where $n \in I$

But usually, we take only that value for which $0 < \theta  < 2\pi $. Any two arguments of a complex number differ by $2{\text{n}}\pi $.

Argument of $z$ will be $\theta ,\pi  - \theta ,\pi  + \theta $ and $2\pi  - \theta $ according as the point $z$ lies in I, II, III and IV quadrants respectively, where $\theta  = {\tan ^{ - 1}}\left| {\dfrac{y}{x}} \right|$

The Argument of a Complex Number

If $z$ is a non-zero complex number represented by the complex plane's point $P$, then the argument of $z$ is the angle formed by $OP$ with the positive direction of the real axis.

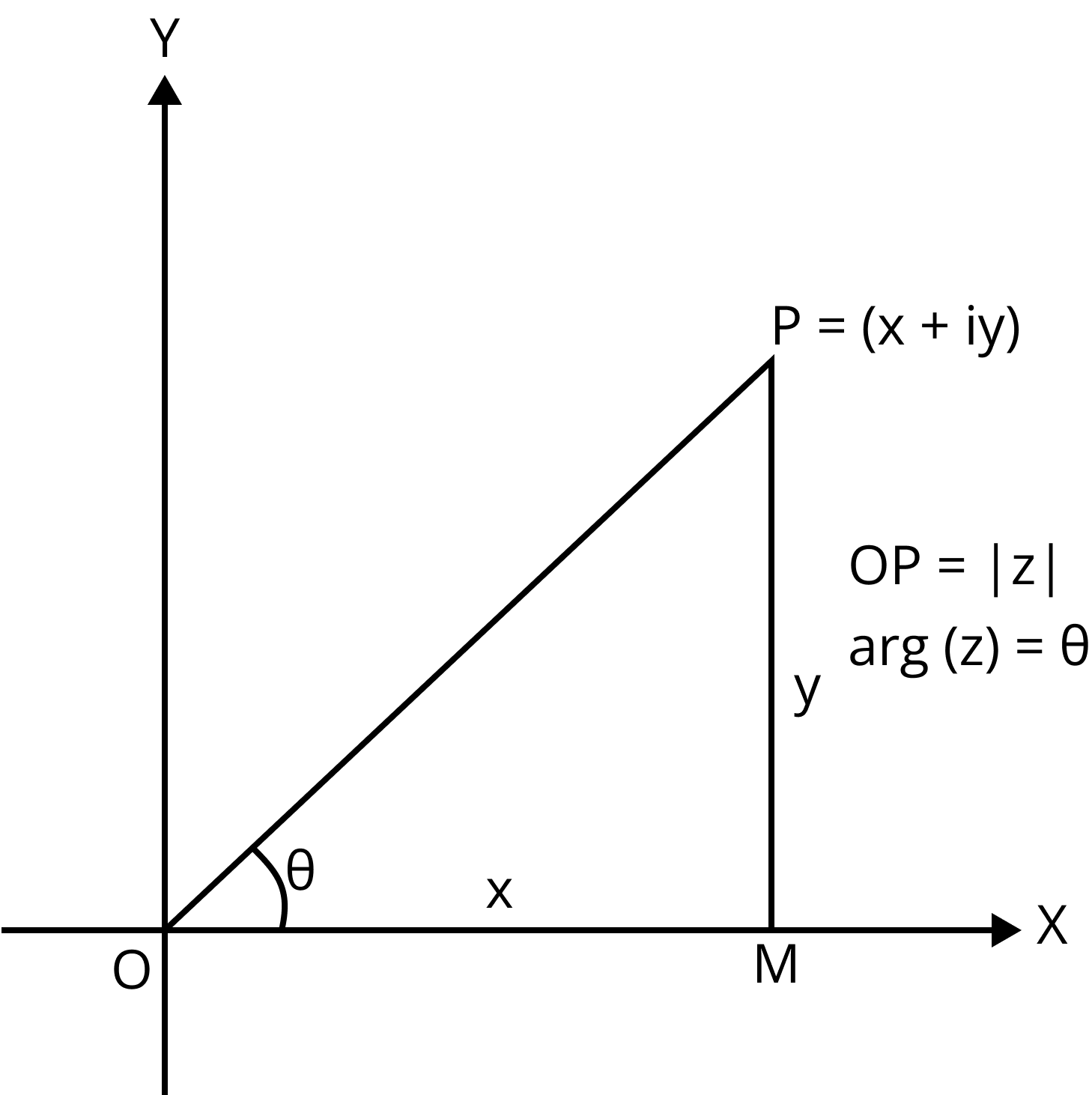
Argument of a Complex Number

Principal Value of the Argument for Different Positions of $z$ in the Complex Plane

1. When $z$ lies in the first quadrant

Argument of a Complex Number in 1st Quadrant

$\arg (z) = {\tan ^{ - 1}}\left( {\dfrac{y}{x}} \right)$

2. When $z$ lies in the second quadrant

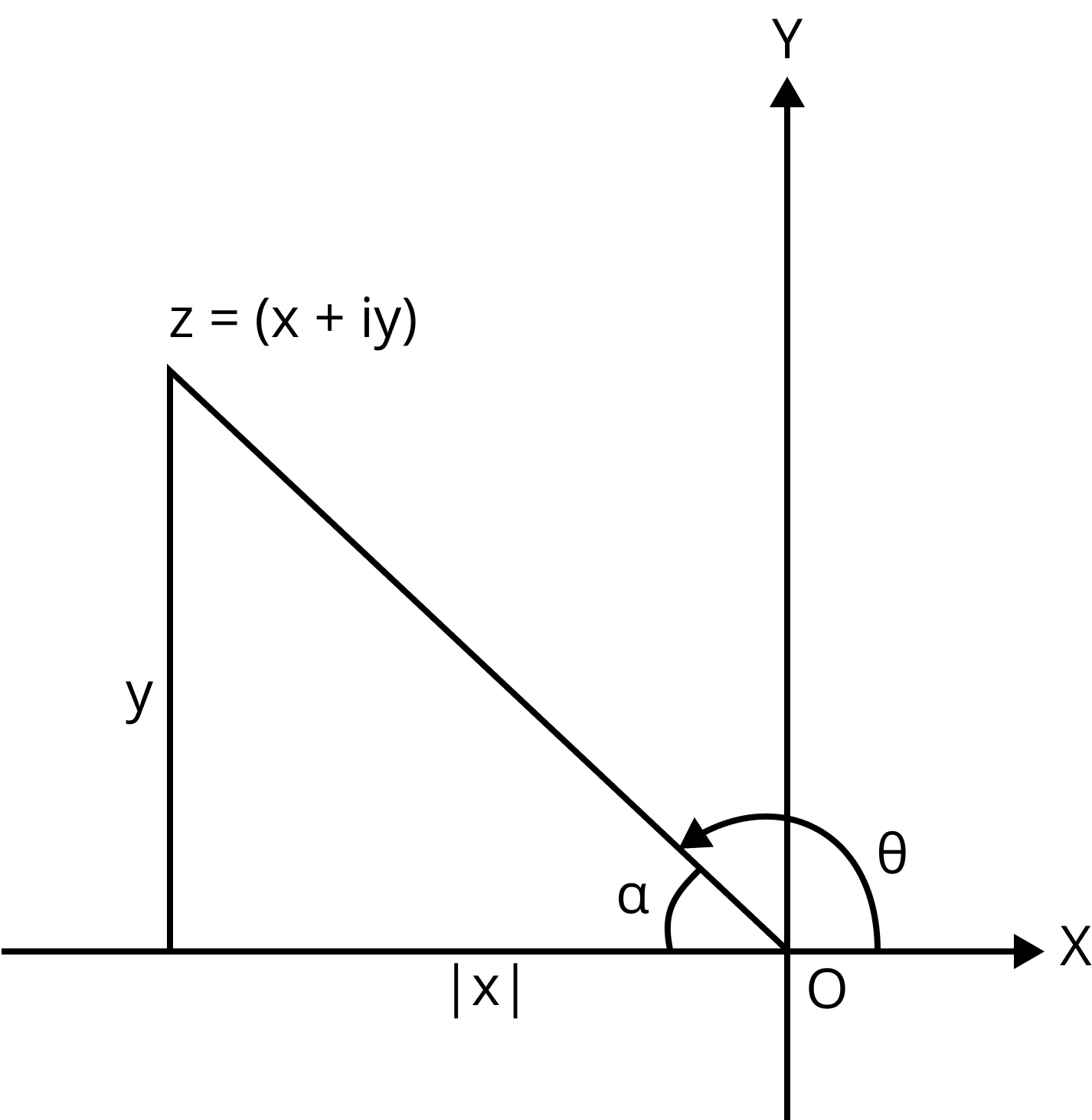
Argument of a Complex Number in 2nd Quadrant

$\arg (z) = \pi  - {\tan ^{ - 1}}\left( {\dfrac{y}{{|x|}}} \right)$

3. When $z$ lies in the third quadrant

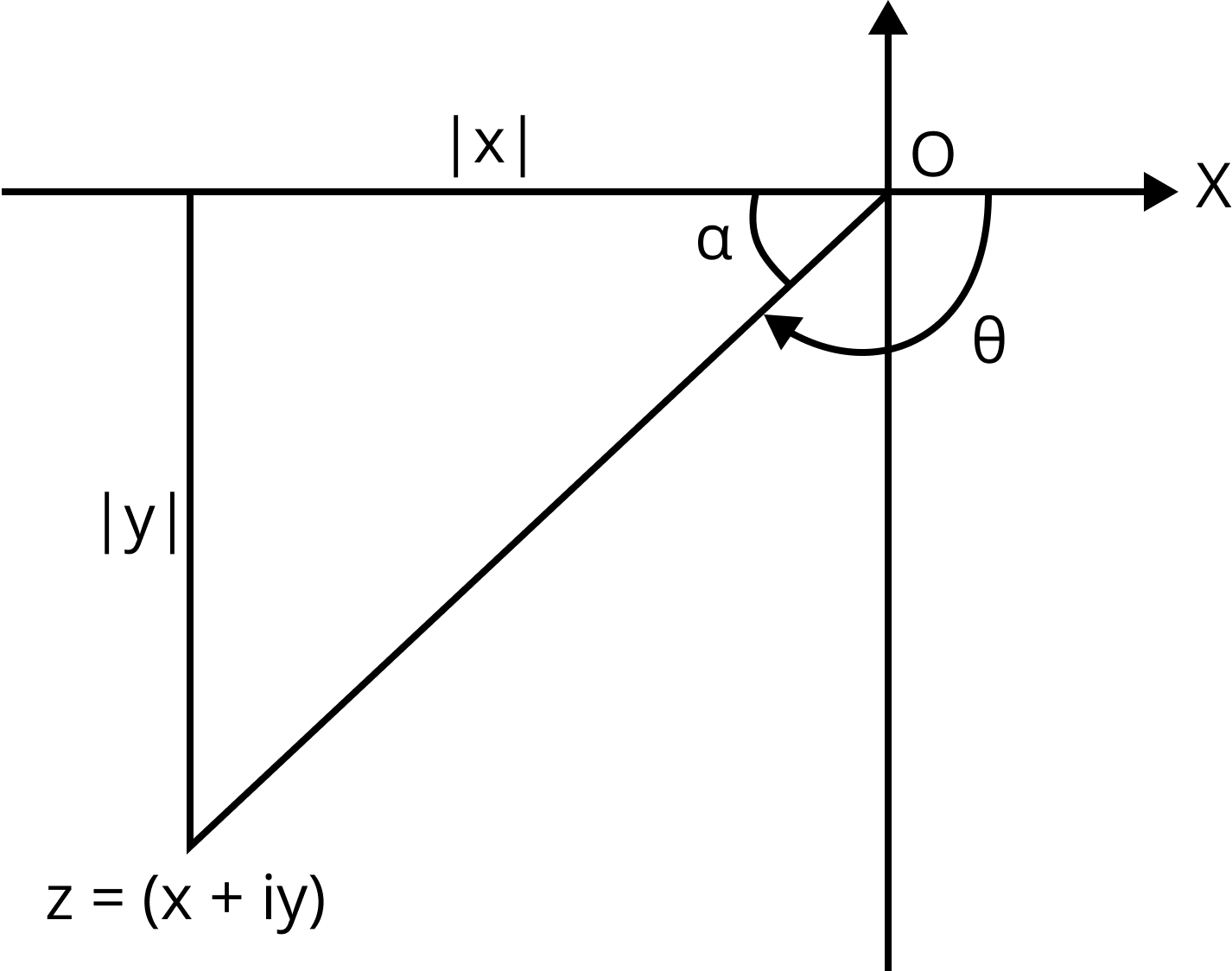
Argument of a Complex Number in 3rd Quadrant

$\arg (z) =  - \pi  + {\tan ^{ - 1}}\left( {\dfrac{{|y|}}{{|x|}}} \right)$

4. When $z$ lies in the fourth quadrant

( Image will be uploaded soon) 

Argument of a Complex Number in 4th Quadrant

$\arg (z) =  - {\tan ^{ - 1}}\left( {\dfrac{{|y|}}{x}} \right)$

Polar Form of a Complex Number

Let $z$ be a non-zero complex number, then we can write

$z = r(\cos \theta  + i\sin \theta )$ where $r = |z|$ and $\theta  = \arg (z)$.

Euler's Formula

The complex number $\cos \theta  + i\sin \theta $ is denoted by ${e^{i\theta }}$ or $\operatorname{cis} \theta $. That is${e^{i\theta }} = \operatorname{cis} \theta  = \cos \theta  + i\sin \theta $

De Moivre's Theorem and its Applications

(a) The Integral Index De Moivre's Theorem 

If $n$ is an integer, then ${(\cos \theta  + i\sin \theta )^n} = \cos (n\theta ) + i\sin (n\theta )$

(b) De Moivre's Theorem for Rational Index.

If $n$ is a rational number, then one of the values of ${(\cos \theta  + i\sin \theta )^n}$ is $\cos (n\theta ) + i\sin (n\theta )$. In fact, if $n = \dfrac{p}{q}$, $p,q \in {\mathbf{I}},q > 0$ and $p,q$ share no factors, then ${(\cos \theta  + i\sin \theta )^n}$ has $q$ distinct values, one of which is $\cos (n\theta ) + i\sin (n\theta )$.

${\mathbf{nth}}$ Roots of Unity

By a root of unity we mean any complex number  which satisfies the equation

We mean any complex number $z$ that satisfies the equation by a $n$th root of unity. 

${z^n} = 1$

Because an equation of degree $n$ has $n$ roots, there are $n$,$z$ values that satisfy the equation (1).

To get these $n$,$z$ values, we write 

$1 = \cos (2k\pi ) + i\sin (2k\pi )$

where $k \in {\mathbf{I}}$ and

$ \Rightarrow z = \cos \left( {\dfrac{{2k\pi }}{n}} \right) + i\sin \left( {\dfrac{{2k\pi }}{n}} \right)$

${\text{where }}\quad k = 0,1,2, \ldots ,n - 1.$

Cube Roots of Unity

Cube roots of unity are given by $1,\omega ,{\omega ^2}$, where

$\omega  = \cos \left( {\dfrac{{2\pi }}{3}} \right) + i\sin \left( {\dfrac{{2\pi }}{3}} \right) = \dfrac{{ - 1 + \sqrt 3 i}}{2}{\text{ and }}{\omega ^2} = \dfrac{{ - 1 - \sqrt 3 i}}{2}$

Some Results Involving Complex Cube Root of Unity $(\omega )$

(i) ${\omega ^3} = 1,\bar \omega  = {\omega ^2}$ and $\dfrac{1}{\omega } = {\omega ^2}$

(ii) $1 + \omega  + {\omega ^2} = 0$

(iii) ${x^3} - 1 = (x - 1)(x - \omega )\left( {x - {\omega ^2}} \right)$

(iv) $\omega $ and ${\omega ^2}$ are roots of ${x^2} + x + 1 = 0$

(v) ${a^3} - {b^3} = (a - b)(a - b\omega )\left( {a - b{\omega ^2}} \right)$

$ = (a - b)\left( {a\omega  - b{\omega ^2}} \right)\left( {a{\omega ^2} - b\omega } \right)$

(vi)${a^2} + {b^2} + {c^2} - bc - ca - ab = \left( {a + b\omega  + c{\omega ^2}} \right)\left( {a + b{\omega ^2} + c\omega } \right)$

(vii) ${a^3} + {b^3} + {c^3} - 3abc = (a + b + c)\left( {a + b\omega  + c{\omega ^2}} \right)\left( {a + b{\omega ^2} + c\omega } \right)$

(viii) ${x^3} + 1 = (x + 1)(x + \omega )\left( {x + {\omega ^2}} \right)$

(ix) ${a^3} + {b^3} = (a + b)(a + b\omega )\left( {a + b{\omega ^2}} \right)$

(x) Cube roots of real number $a$ are ${{a}^{\dfrac{1}{3}}},{{a}^{\dfrac{1}{3}}}\omega ,{{a}^{\dfrac{1}{3}}}{{\omega }^{2}}$.

Geometric Interpretation of Multiplying a Complex Number By ${{\text{e}}^{i\alpha }}$

Let $z$ be a complex number that is not zero. In the polar form, $z$ can be written as follows: 

$z = r(\cos \theta  + i\sin \theta ) = r{e^{i\theta }}$

where $r = |z|$ and $\arg (z) = \theta $

We have

$z{e^{i\alpha }} = r{e^{i\theta }}{e^{i\alpha }} = r{e^{i(\theta  + \alpha )}}$

Thus, $z{e^{i\alpha }}$ denotes a complex number with modulus $r$ and argument $\theta  + \alpha $. Geometrically, $z{e^{i\alpha }}$can be obtained by rotating the segment joining $O$ and $P(z)$ through an anticlockwise angle $\alpha $. 

Solved Example:

1. Let $p$ and $q$ be two complex numbers such that $q \ne 0$. If the roots of the equation ${x^2} + px + {q^2} = 0$ have the same absolute value, then $p/q$ is

1. an integer

2. a rational number

3. a real number

4. a complex number.

Ans. (c)

Solution: Let ${x_1},{x_2}$ be the roots of ${x^2} + px + {q^2} = 0$ and $\left| {{x_1}} \right| = \left| {{x_2}} \right| = r$. 

Note that ${x_1}{x_2} = {q^2} \ne 0$. Now,

$\dfrac{{{p^2}}}{{{q^2}}} = \dfrac{{{{\left( {{x_1} + {x_2}} \right)}^2}}}{{{x_1}{x_2}}} = \dfrac{{{x_1}}}{{{x_2}}} + \dfrac{{{x_2}}}{{{x_1}}} + 2$

$ = \dfrac{{{x_1}{{\bar x}_2}}}{{{{\left| {{x_2}} \right|}^2}}} + \dfrac{{{{\bar x}_1}{x_2}}}{{{{\left| {{x_1}} \right|}^2}}} + 2 = \dfrac{1}{{{r^2}}}\left( {{x_1}{{\bar x}_2} + {{\bar x}_1}{x_2}} \right) + 2$

$= \dfrac{2}{{{r^2}}}\operatorname{Re} \left( {{x_1}{{\bar x}_2}} \right) + 2$

$ \Rightarrow \dfrac{{{p^2}}}{{{q^2}}}{\text{ is a real number}}{\text{.}}$

${\text{ Next, as }} - \operatorname{Re} \left( {{x_1}{{\bar x}_2}} \right) \leqslant \left| {{x_1}{{\bar x}_2}} \right| = \left| {{x_1}{x_2}} \right| = \left| {{x_1}} \right|\left| {{x_2}} \right| = {r^2}$

$ \Rightarrow \dfrac{{{p^2}}}{{{q^2}}} \geqslant  - \dfrac{{2{r^2}}}{{{r^2}}} + 2 =  - 2 + 2 = 0$

Therefore, $\dfrac{p}{q}$ is a real number.

2. If $\omega $ is an imaginary cube root of unity, then value of the expression

$2(1 + \omega )\left( {1 + {\omega ^2}} \right){\text{ }} + 3(2 + \omega )\left( {2 + {\omega ^2}} \right) +  \ldots . + (n + 1)(n + \omega )\left( {n + {\omega ^2}} \right)$ is

1. $\dfrac{1}{4}{n^2}{(n + 1)^2} + n$

2. $\dfrac{1}{4}{n^2}{(n + 1)^2} - n$

3. $\dfrac{1}{4}n{(n + 1)^2} - n$

4. $\dfrac{1}{4}{n^2}{(n + 1)^2} - 2n$

Ans. (a)

Solution: $r$ th term of the given expression is

$(r + 1)(r + \omega )\left( {r + {\omega ^2}} \right) = {r^3} + 1$

$\therefore $ value of the given expression is

$\sum\limits_{r = 1}^n {\left( {{r^3} + 1} \right)}  = \dfrac{1}{4}{n^2}{(n + 1)^2} + n$

Quadratic Equations

A formula of the quadratic form is $a{x^2} + bx + c = 0$........(1)

A quadratic equation is defined as $a \ne 0,a,b,c \in {\mathbf{C}}$, the set of real numbers. 

The discriminant of the equation is the quantity $D = {b}^2 - 4ac$

A complex number $\alpha $ such that $a{\alpha ^2} + b\alpha  + c = 0$ is a root of the quadratic equation (1).

The quadratic formula gives the roots of equation (1)

$x = \dfrac{{ - b \pm \sqrt D }}{{2a}}$

Nature of Roots

1. If $a,b,c \in {\mathbf{R}}$ and $a \ne 0$.  Then the following are true:

• If and only if $D > 0$ the equation (1) has real and distinct roots.

• If and only if $D = 0$, the equation (1) has real and equal roots.

• If and only if $D < 0$, the equation (1) has complex roots with non-zero imaginary parts.

• If and only if $p + iq(p,q \in {\mathbf{R}},q \ne 0)$ is a root then $p - iq$ is a root of equation (1). 

2. If $a,b,c \in {\mathbf{Q}}$ are rational numbers and $D$ is a perfect square of a rational number, then equation (1) has rational roots. 

3. If $a,b,c \in {\mathbf{Q}}$ and $p + \sqrt q (p,q \in {\mathbf{Q}})$ are irrational roots of equation (1), then $p - \sqrt q $ is also an irrational root of equation (1).

4. If the set of integers, $a = 1,b,c \in {\mathbf{I}}$, and the roots of equation (1) are rational numbers, then these roots must be integers.

5. If more than two distinct complex numbers satisfy equation (1), equation (1) becomes an identity, that is, $a = b = c = 0$. 

Relation Between Roots and Coefficients

If $\alpha $ and $\beta $ are the quadratic equation's roots (1), then 

$\alpha  + \beta  =  - \dfrac{b}{a}$

and

$\alpha \beta  = \dfrac{c}{a}$

It is worth noting that a quadratic equation with roots $\alpha $ and $\beta $ is given by 

$(x - \alpha )(x - \beta ) = 0$

Quadratic Expression and Its Graph

Let $f(x) = a{x^2} + bx + c$, where $a,b,c \in {\mathbf{R}}$ and $a \ne 0$

We have $f(x) = a\left[ {{x^2} + \dfrac{b}{a}x + \dfrac{c}{a}} \right]$

$ = a\left[ {{x^2} + \dfrac{b}{a}x + \dfrac{{{b^2}}}{{4{a^2}}} + \dfrac{c}{a} - \dfrac{{{b^2}}}{{4{a^2}}}} \right]$

$ = a\left[ {{{\left( {x + \dfrac{b}{{2a}}} \right)}^2} + \dfrac{{4ac - {b^2}}}{{4{a^2}}}} \right]\,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ............(2)$

When is a Quadratic Expression always positive and when is it always negative? 

It follows from (2) that $f(x) > 0( < 0)\forall x \in {\mathbf{R}}$ if and only if $a > 0( < 0)$ and $D = {b^2} - 4ac < 0$. Also, it follows from (2) that $f(x) \geqslant 0( \leqslant 0)\forall x \in {\mathbf{R}}$ if and only if $a > 0( < 0)$ and $D = {b^2} - 4ac = 0$. In this case $f\left( x \right) > 0\left( { < 0{\text{ }}} \right)$for each $x \in {\mathbf{R}},x \ne  - b/2a$. 

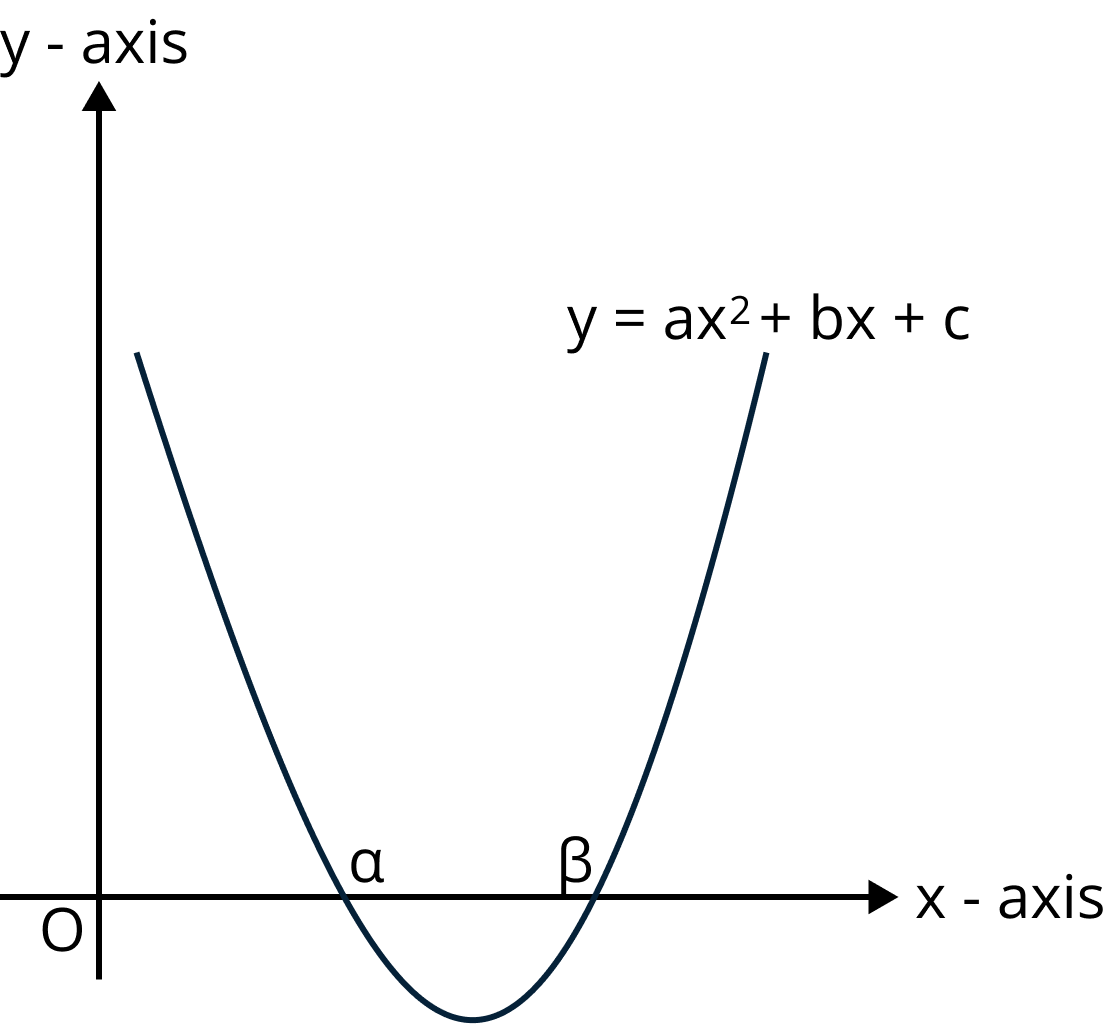
Quadratic Expression

Position of Roots of a Quadratic Equation

Let $f(x) = a{x^2} + bx + c$ be a quadratic expression in $a,b,c \in {\mathbf{R}}$ and let $k$ be a real number. 

Conditions for both roots to be greater than a Real Number $k.$

If  then the parabola opens upwards and intersects the -axis in where

If $a > 0$ and ${b^2} - 4ac > 0$ the parabola $y = a{x^2} + bx + c$ rises and intersects the $x$-axis in $\alpha $ and $\beta $ 

$\alpha ,\beta  = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}$

In this case both the roots $\alpha$ and $\beta$ will be more than $k$ if $k$ lies to the left of both $\alpha$ and $\beta$. 

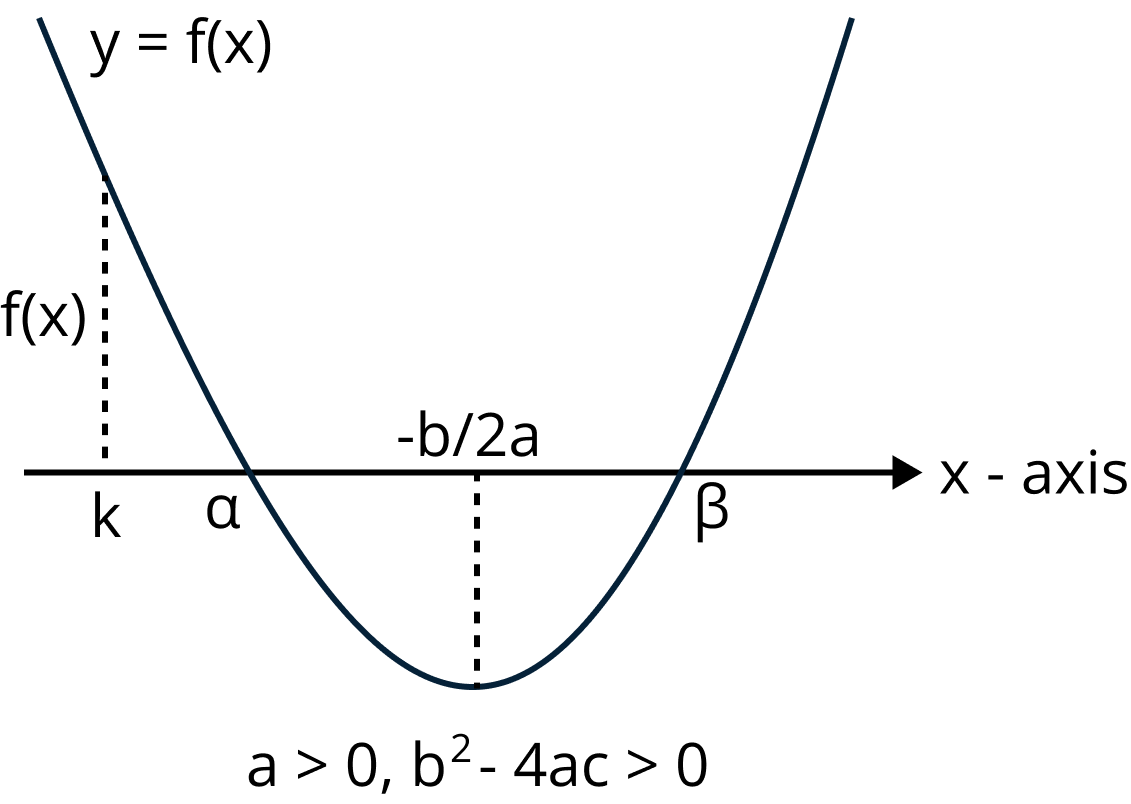
Case

Conditions for a number $k$ to lie between the roots of a quadratic equation

A real number $k$ lies between the roots of the quadratic equation $f(x) = a{x^2} + bx + c = 0$ if and only if $a$ and $f(k)$ are of opposite signs, that is, if and only if

(i) $a > 0$              (ii) $D > 0$              (iii) $f(k) < 0$ 

(i) $a < 0$               (ii) $D > 0$                (iii) $f(k) > 0$ 

Combining, we may say $k$ lies between the roots of $f(x) = a{x^2} + bx + c = 0$  if and only if

(i) $D > 0$                     (ii) $af(k) < 0$

Descartes Rule of Signs for the Roots of a Polynomial

• Rule 1: A polynomial equation's maximum number of positive real roots 

$f(x) = {a_0}{x^n} + {a_1}{x^{n - 1}} + {a_2}{x^{n - 2}} +  \ldots  + {a_{n - 1}}x + {a_n} = 0$

is the number of times the sign of a coefficient changes from positive to negative and from negative to positive. 

For Example, in the equation ${x^3} + 3{x^2} + 7x - 11 = 0$ the coefficient signs are $++-$

Because there is only one sign change, the number of positive roots of ${x^3} + 3{x^2} + 7x - 11 = 0$  can only be one.

• Rule 2: The polynomial equation's maximum number of negative roots is $f\left( x \right) = 0$. denotes the number of changes in the signs of the coefficients of the equation $f\left( { - x} \right) = 0$from positive to negative and negative to positive.

Polynomial and Polynomial Equation

An expression of the form  ${a_0}{x^n} + {a_1}{x^{n - 2}} + ...... + {a_{n - 1}}x + {a_n}$  where  ${a_0},{a_1},{a_2}......{a_n}$  are constants (${a_0} \ne 0$) and n is a positive integer is called a polynomial in x of degree n.

If f (x) is a real or complex polynomial, then f(x) = 0 is known as a polynomial equation.

Sequences

A sequence is a function with the set of natural numbers as its domain. A sequence is called a real sequence if its range is a subset of real numbers (complex numbers) (complex sequence). 

If $f:{\mathbf{N}} \to {\mathbf{C}}$ is a sequence, it is usually denoted by $\langle f(1),f(2),f(3), \cdots \rangle  = \langle f(n)\rangle $. 

If ${t_n} = f(n)$, the sequence is written as $\left\langle {{t_1},{t_2},{t_3}, \cdots } \right\rangle $. 

Arithmetic Progression

When the difference ${t_n} - {t_{n - 1}}$ is a constant for all $n \in {\mathbf{N}},n > 1$a sequence of numbers $\left\langle {{t_n}} \right\rangle $ is said to be in arithmetic progression (A.P.). This constant is known as the A.P. common difference, usually denoted by the letter $d$. 

If $a$ is the first term and $d$ the common difference of the A.P., then its $n$th term ${t_n}$ is given by

${t_n} = a + (n - 1)d$

${t_n} = {t_m} + (n - m)d$

The sum ${S_n}$ of the first $n$ terms of such an A.P. is given by

${S_n} = \dfrac{n}{2}[2a + (n - 1)d] = \dfrac{n}{2}(a + l)$

where $l$ is the last term, that is, the $n$th term of the A.P.

Properties of Arithmetic Progression

• If a constant is added or subtracted from each term of an AP, then the resulting sequence is also an AP with the same common difference.

• If each term of a given AP is multiplied or divided by a non-zero constant $k$, then the resulting sequence is also an AP with common difference $kd$or $\dfrac{d}{k}$, where $d$ is the common difference of the given AP.

• A sequence is an AP if its $n$th term is of the form $An + B$, i.e. a linear expression in $n$.

• In a finite AP the sum of the terms equidistant from the beginning and end is always the same.

i.e. ${a_1} + {a_n} = {a_2} + {a_{n - 1}} = {a_3} + {a_{n - 2}} =  \ldots $

Geometric Progression (G.P.)

A Geometric Progression is a sequence in which the initial term is non-zero and each subsequent term is r times the preceding term, where r is some fixed non-zero number known as the G.P. 's common ratio.

${n^{th}}$term of G.P. $\left( {{t_n}} \right)$

${t_n} = a{(r)^{n - 1}},n \in N$

Sum of first n terms of a GP $\left( {{S_n}} \right):$

${S_n} = \dfrac{{a\left( {{r^n} - 1} \right)}}{{r - 1}},r \ne 1$

$= na{\text{               }},r = 1$

$= 0{\text{                 }},r =  - 1{\text{ and }}n{\text{ is even}}$

$= a{\text{                 ,}}r =  - 1{\text{ and }}n{\text{ is odd}}$

Sum of infinite terms in G.P.

If $ - 1 < r < 1$, then the sum of the infinite G.P. $a + ar + a{r^2} +  \ldots $

${S_\infty } = \dfrac{a}{{1 - r}}$

Harmonic Progression

The sequence ${a_1},{a_2}, \cdots ,{a_n}, \cdots $ where ${a_i} \ne 0$ for each $i$ is said to be in harmonic progression (H.P.) if the sequence $\dfrac{1}{{{a}_{1}}},\dfrac{1}{{{a}_{2}}},........,\dfrac{1}{{{a}_{n}}}$, the $n$th term of the H.P., is given by

${a_n} = \dfrac{1}{{a + (n - 1)d}}$ where $a = \dfrac{1}{{{a_1}}}$ and $d = \dfrac{1}{{{a_2}}} - \dfrac{1}{{{a_1}}}$

Summation of Some Series Of Natural Numbers

• $\sum\limits_{k = 1}^n k  = 1 + 2 + 3 +  \cdots  + n = \dfrac{1}{2}n(n + 1)$

• $\sum\limits_{k = 1}^n {{k^2}}  = {1^2} + {2^2} +  \cdots  + {n^2} = \dfrac{1}{6}n(n + 1)(2n + 1)$

• $\sum\limits_{k = 1}^n {{k^3}}  = {1^3} + {2^3} +  \cdots  + {n^3} = {\left( {\sum\limits_{k = 1}^n k } \right)^2}$ $ = {(1 + 2 + 3 +  \cdots  + n)^2}$

• $ = {\left[ {\dfrac{1}{2}n(n + 1)} \right]^2} = \dfrac{1}{4}{n^2}{(n + 1)^2}$

Sum of the Products of Two Terms of a Sequence

To obtain the sum $\sum\limits_{i < j} {{a_i}} {a_j}$, we use the identity $2\sum\limits_{i < j} {{a_i}} {a_j} = {\left( {{a_1} + {a_2} +  \ldots  + {a_n}} \right)^2} - \left( {a_1^2 + a_2^2 +  \ldots  + a_n^2} \right)$

Method of Difference for Summation of Series

If possible, express $r$ th term as the difference of two terms as follows:

${t_r} = f(r) - f(r \pm 1).$

Logarithms

Exponential Function

For $x \in {\mathbf{R}}$, we define

${e^x} = 1 + x + \dfrac{{{x^2}}}{{2!}} + \dfrac{{{x^3}}}{{3!}} +  \ldots  + \dfrac{{{x^n}}}{{n!}} +  \ldots  = \sum\limits_{n = 0}^\infty  {\dfrac{{{x^n}}}{{n!}}} $

It can be proved for every $x \in {\mathbf{R}}$, the number ${e^x}$ is a finite number. We call ${e^x}$ the exponential function.

Properties

• ${e^x}$ is defined for each $x \in {\mathbf{R}}$.

• ${e^x} > 0$ for all $x \in {\mathbf{R}}$.

• ${e^0} = 1$.

• If $a,b \in {\mathbf{R}},a < b$ then ${e^a} < {e^b}$.

• ${e^x} \times {e^y} = {e^{x + y}}$ for all $x,y \in {\mathbf{R}}$.

• $\dfrac{{{e^x}}}{{{e^y}}} = {e^{x - y}}$ for all $x,y \in {\mathbf{R}}$

• ${\left( {{e^x}} \right)^y} = {e^{xy}}$ for all $x,y \in {\mathbf{R}}$.

• For each positive real number $x$ there exists one and only one real number $y$ such that ${e^y} = x$.

• ${e^x}$ is one to one function.

Logarithm

Given a positive real number $x$, there is only one real number $y$ such that ${e^y} = x$; we refer to this number $y$ as $\log x$ or ${\log _e}x$. The symbol $\ln x$ also represents the logarithm. 

In general, the logarithm to the base of the number $x(x > 0)$ is the number $y$ such that ${a^y} = x$. Thus, $y = {\log _a}x$ denotes ${a^y} = x$. ${\log _{10}}x$ is known as the common logarithm for $a = 10,$ and ${\log _e}x$ is known as the natural logarithm for $a = e,$. 

Properties of Logarithms

• ${\log _a}1 = 0,a > 0,a \ne 1$.

• ${\log _a}a = 1,a > 0,a \ne 1$.

• ${\log _e}{e^x} = x\forall x \in {\mathbf{R}}$ and ${e^{{{\log }_e}x}} = x\forall x > 0$ i.e. ${\log _e}x$ is the inverse function of exponential function ${e^x}$.

• ${\log _a}(xy) = {\log _a}x + {\log _a}y$ for all $x,y > 0$ and $a > 0,a \ne 1$.

• ${{\log }_{a}}(\dfrac{1}{x})=-{{\log }_{a}}x\forall x>0,a>0,a\ne 1$.

• ${{\log }_{a}}(\dfrac{x}{y})={{\log }_{a}}x-{{\log }_{a}}y,x,y>0,a>0$, $a \ne 1.$

• If $a \in {\mathbf{R}}$ and $x > 0$, then we define ${x^a} = {e^{a{{\log }_e}x}} = \sum\limits_{n = 0}^\infty  {{{\left( {a{{\log }_e}x} \right)}^n}} $

• $\log {x^y} = y\log x\forall x > 0,y \in {\mathbf{R}}$.

• (Change of base formula) If $a > 0,a \ne 1$ then ${\log _a}x = \dfrac{{{{\log }_e}x}}{{{{\log }_e}a}}.$ In fact if $a,b,c > 0$ and $a,c \ne 1$ then ${\log _a}b = \dfrac{{{{\log }_c}x}}{{{{\log }_c}a}}$,

• If $a > 1$ and $0 < x < y$ then ${\log _{ax}}x < {\log _a}y$ (i.e. ${\log _a}x$ is an increasing function). In particular if $x > 1$ then ${\log _a}x > 0$ and if $0 < x < 1$ then ${\log _a}x < 0$.

• Logarithmic Inequalities

• For $\varphi (x) > 1,{\log _{\varphi (x)}}f(x) \geqslant {\log _{\varphi (x)}}g(x)$ $ \Leftrightarrow f(x) \geqslant g(x) > 0$

• For $0 < \varphi (x) < 1,{\log _{\varphi (x)}}f(x) \geqslant {\log _{\varphi (x)}}g(x)$ $ \Leftrightarrow 0 < f(x) \leqslant g(x)$

• For $\varphi (x) > 1,{\log _{\varphi (x)}}f(x) \geqslant a$ $ \Leftrightarrow f(x) \geqslant {a^{\varphi (x)}}$

• For $0 < \varphi (x) < 1,{\log _{\varphi (x)}}f(x) \geqslant a$ $ \Leftrightarrow 0 < f(x) \leqslant {a^{\varphi (x)}}$

Permutation and combination

Fundamental Principles of counting

The Sum Rule

Assume that $A$ and $B$ are two disjoint (mutually exclusive) events that never occur together. Assume that $A$ occurs in $m$ ways and $B$ occurs in $n$ ways. Then $A$ or $B$  can happen in $m + n$ different ways. This rule can also be applied to events that are not mutually exclusive. 

The Product Rule

Assume an event $X$ can be divided into two stages, $A$ and $B$. Assume that stage $A$ occurs in $m$ different ways and that these stages are unrelated in the sense that stage $B$ occurs in $n$ different ways regardless of the outcome of stage $A.$ Then event $X$ occurs in $mn$ different ways. This rule applies even if event $X$ can be divided into more than two stages. 

Permutation

Each arrangement which can be made by taking some or all of several things is called a permutation. Thus, in permutation, the order of arrangement is important. When the order is changed, a different permutation is obtained.

e.g The permutation of three letters A, B and C taking all at a time are $ABC,ACB,{\text{ }}BCA,BAC,CBA$ and $CAB$.

Conditions of Permutation:

1) The number of all permutations of n different objects taking r at a time.

(i) when a particular object is always included is r ${}^{n - 1}{P_{r - 1}}$.

(ii) when a particular object is never included is ${}^{n - 1}{P_r}$.

2) Number of permutations of n different things, taken r at a time, when s particular things are to be always included in each arrangement, is ${}^{n-s}{{C}_{r-s}}$

3) Number of permutation of n different things, taken all at a time , when m specified  things always come together , is $m! \times (n - m + 1)!$

4) Number of permutation of n different things, taken all at a time , when m specified  things never come together $n! - m! \times (n - m + 1)!$

5) The number of permutation of  n things , of which ${p_1}$ are alike of one kind ;${p_2}$are alike of second kind; ${p_3}$ are alike of third kind;….;${p_r}$ are alike of r 3th kind such that

${p_1} + {p_2} +  \ldots  + {p_r} = n{\kern 1pt} {\kern 1pt} {\kern 1pt} \,is{\kern 1pt} \,{\kern 1pt} \,\dfrac{{n!}}{{{p_1}!{p_2}!{p_3}! \ldots {p_r}!}}$

Combinations:

Each of the different selections made by taking some or all of a number of objects,(irrespective of there arrangements) is called a combinations , e.g. The different combinations formed of two out of three letters $A,B,C$are $AB,AC,BC$.

The number of combinations of n different things taken r at a time is denoted by 

 ${}^n{C_r}\,{\kern 1pt} \,{\text{or}}{\kern 1pt} \,\,\,C(n,r){\kern 1pt} \,{\kern 1pt} $

Then, ${}^n{C_r} = \dfrac{{n!}}{{r!(n - r)!}} = \dfrac{{{}^n{P_r}}}{{r!}}[0 \leqslant r \leqslant n]$

$ = \dfrac{{n(n - 1)(n - 2).....(n - r + 1)}}{{r(r - 1)(r - 2)...2,1}},n \in N\,{\kern 1pt} {\text{and }}r \in W$

If , r>n ,then ${}^n{C_r} = 0$

Properties:

(i) ${}^n{C_r}$ is a natural number.

(ii) ${}^n{C_r} = {}^n{C_{n - r}},$ for $0 \leqslant r \leqslant n$

(iii) ${}^n{C_0} = {}^n{C_n} = 1,{}^n{C_1} = n$

(iv) Let n and r be non-negative integers such that $r \leqslant n$.

Then, ${}^n{C_r} + {}^n{C_{r - 1}} = {}^{n + 1}{C_r}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} [{\text{Pascal's law}}]$

${}^n{C_r} = \dfrac{n}{r}{}^{n - 1}{C_{r - 1}}[1 \leqslant r \leqslant n]$

(v)If $1 \leqslant r \leqslant n$ ,then $n.{}^{n - 1}{C_{r - 1}} = (n - r + 1){}^n{C_{r - 1}}$.

(vi) ${}^n{C_x} = {}^n{C_y} \Rightarrow x = yorx + y = n$

(vii) $\dfrac{^{n}{{C}_{r}}}{^{n}{{C}_{r-1}}}=\left( \dfrac{n-r+1}{r} \right)$

(viii) ${}^n{C_0} + {}^n{C_1} + {}^n{C_2} + ..... + {}^n{C_n} = {2^n}$

(ix) ${}^n{C_0} + {}^n{C_2} + {}^n{C_4} + ..... = {}^n{C_1} + {}^n{C_3} + {}^n{C_5}..... = {2^{n - 1}}$

(x) ${}^{2n + 1}{C_0} + {}^{2n + 1}{C_1} + {}^{2n + 1}{C_2} + .... + {}^{2n + 1}{C_n} = {2^{2n}}$

Circular Permutation

There are $(n-1)!$ ways to arrange $n$ distinct objects around a circle. 

(i) Here, anti-clockwise and clockwise order of arrangements are considered as distinct permutations.

(ii) If anti-clockwise and clockwise order of arrangements are not distinct, e.g. arrangement of beads in a necklace, arrangement of flowers in a garland etc. then number of circular permutations of n distinct items is $\dfrac{(n-1)!}{2}$ . 

(iii) The number of circular permutations of $n$ different things taken $r$ at a time, when clockwise and anti-clockwise orders are taken as different is $\dfrac{\left( ^{\text{n}}{{\text{P}}_{\text{r}}} \right)}{\text{r}}$, for $1\le \text{r}\le \text{n}$

(iv) The number of circular permutations of $n$ different things taken $r$ at a time, when clockwise and anti-clockwise orders are taken as same is $\dfrac{\left( ^{n}{{P}_{\text{r}}} \right)}{2\text{r}}$.

Division of Identical Objects

The number of ways to distribute $n$ identical objects among $r$ people while giving zero or more to each is equal to the number of ways to arrange $n$ identical objects of one kind and $(r-1)$ identical objects of the second kind (separators) in a row $=\dfrac{(n+r-1) !}{n !(r-1) !}={ }^{\mathrm{n}+\mathrm{r}-1} C_{\mathrm{r}-1}$

Derangement

The number of ways to arrange $n$ objects numbered $1,2,3, \ldots$, $n$at $n$places numbered $1,2,3, \ldots, n$ so that no object goes to the place corresponding to its number is $n !\left(\dfrac{1}{2 !}-\dfrac{1}{3 !}+\dfrac{1}{4 !}-\cdots+(-1)^{n-1} \dfrac{1}{n !}\right)$

Binomial Theorem

Binomial theorem for a positive integral index

Suppose $n$ is a positive integer and $x,y$are two complex numbers. 

${{(x+y)}^{n}}{{=}^{n}}{{C}_{0}}{{x}^{n}}{{+}^{n}}{{C}_{1}}{{x}^{n-1}}y{{+}^{n}}{{C}_{2}}{{x}^{n-2}}{{y}^{2}}+\ldots {{+}^{n}}{{C}_{r}}{{x}^{n-r}}{{y}^{y}}+\ldots {{+}^{n}}{{C}_{n-1}}x{{y}^{n-1}}{{+}^{n}}{{C}_{n}}{{y}^{n}}................(1)$

The coefficients ${ }^{n} C_{0},{ }^{n} C_{1}, \cdots,{ }^{n} C_{n}$ are called binomial coefficients.

Properties of Binomial Expansion

1. The expansion contains $(n+1)$terms (1). 

2. The sum of the exponents of $x$and $y$in any term of (1) is always $n.$

3. Binomial coefficients of terms equidistant from the beginning and end are equal, because ${ }^{n} C_{r}={ }^{n} C_{n-r}$ $(0 \leq r \leq n)$

4. The term ${ }^{n} C_{r} x^{n-r} y^{n}$ is the $(r+1)$ th term from the beginning of the expansion. It is usually denoted by $T_{r+1}$ and is called the general term of the expansion.

Middle Terms

1. $\boldsymbol{n}$ is even

If $n$ is even, then the expansion (1) has just one middle term, viz. $\left(\dfrac{n}{2}+1\right)$ th term. It is given by $^{n}{{C}_{n/2}}{{x}^{\dfrac{n}{2}}}{{y}^{\dfrac{n}{2}}}.$

2. $\boldsymbol{n}$ is odd

If $n$ is odd, then the expansion (1) has two middle terms, viz. $\left(\dfrac{n+1}{2}\right)$ th term and $\left(\dfrac{n+1}{2}+1\right)$ th term. 

The Greatest Coefficient

If $n$ is an even number, the greatest coefficient in the expansion of $(x+y)^{n}$ is $^{n}{{C}_{\dfrac{n}{2}}}$.

If $n$ is an odd number, the expansion of $(x+y)^{n}$ has two greatest coefficients. These are $^{n}{{C}_{\dfrac{n-1}{2}}}$ and $^{n}{{C}_{\dfrac{n+2}{2}}}$, respectively. 

The Greatest Term

To find the greatest term in the expansion of $(x+y)^{n}$, $x, y>0, n \in N$ put

$\alpha=\dfrac{(n+1) y}{x+y}$

If $\alpha$ is not an integer, then the expansion of $(x+y)^{n}$ has just one greatest term and it is given by $k=[\alpha]$ where $[\alpha]$ denotes the greatest integer $\leq \alpha$.

If $\alpha$ is an integer, then expansion of $(x+y)^{n}$ has two greatest terms viz. $\alpha$ th and $(\alpha+1)$ th terms.

Some Other Useful Expansions

In the following expansions $C_{r}$ stands for ${ }^{n} C_{r}$

1. $(x+y)^{n}+(x-y)^{n}$

$=2\left[C_{0} x^{n}+C_{2} x^{n-2} y^{2}+C_{4} x^{n-4} y^{4}+\ldots\right]$

2. $(x+y)^{n}-(x-y)^{n}$

$=2\left[C_{1} x^{n-1} y+C_{3} x^{n-3} y^{3}+C_{5} x^{n-5} y^{5}+\ldots\right]$

3. $n(n-1)(n-2)\ldots (n-k+1){{(x+y)}^{n-k}}=\sum\limits_{r=k}^{n}{r}(r-1)(r-2)\ldots (r-k+1){{C}_{r}}{{x}^{r-k}}{{y}^{n-r}}$

4. $(1+x)^{n}+(1-x)^{n}=2\left[C_{0}+C_{2} x^{2}+C_{4} x^{4}+\ldots\right]$

5. $(1+x)^{n}-(1-x)^{n}=2\left[C_{1} x+C_{3} x^{3}+\ldots .\right]$

6. $C_{1}+2 C_{2} x+3 C_{3} x^{2}+\ldots .+n C_{n} x^{n-1}$ $=n(1+x)^{n-1}$

7. ${{C}_{0}}x+{{C}_{1}}\dfrac{{{x}^{2}}}{2}+{{C}_{2}}\dfrac{{{x}^{3}}}{3}+\ldots .+{{C}_{n}}\dfrac{{{x}^{n+1}}}{n+1}=\int_{0}^{x}{{{(1+t)}^{n}}}dt$

Some Properties of the Binomial Coefficients

1. $C_{0}+C_{1}+C_{2}+\ldots .+C_{n}=2^{n}$

2. $C_{0}+C_{2}+C_{4}+\ldots=C_{1}+C_{3}+C_{5}+\ldots=2^{n-1}$

3. $C_{0}-C_{1}+C_{2}-\ldots+(-1)^{n} C_{n}=0$

4. For $n>1$,$C_{1}-2 C_{2}+3 C_{3}-\ldots .+(-1)^{n-1} n C_{n}=0$

5. If $P_{n}=C_{0} C_{1} C_{2} \ldots C_{n}$, then $\dfrac{P_{n+1}}{P_{n}}=\dfrac{(n+1)^{n}}{n !}$

Multinomial Theorem

If we want to expand $(x+y+z)^{n}$ (where $n$ is a positive integer and $x,y,z$are complex numbers), we can take $y+z=a,$expand the binomial $(x+a)^{n}$, and then expand $(y+z)^{r}$ in each term of $(x+a)^{n}$. In general, we get the following outcome: 

$\left(a_{1}+a_{2}+\ldots+a_{m}\right)^{n}=\sum \dfrac{n !}{n_{1} ! n_{2} ! \cdots n_{m} !} a_{1}^{n_{1}} a_{2}^{n_{2}} \cdots a_{m}^{n_{m}}$$\text{where the summation is taken over all non-negative integers}$${{n}_{1}},{{n}_{2}},\ldots ,{{n}_{m}}$such that $n_{1}+n_{2}+\cdots+n_{m}=n$. 

The number of distinct terms in the expansion (1) is ${ }_{n+m-1} C_{m-1}$

Some Particular Expansions

For $|x|<1$

1. $(1+x)^{-1}=1-x+x^{2}-x^{3}+x^{4}-\ldots .$

2. $(1-x)^{-1}=1+x+x^{2}+x^{3}+x^{4}+\ldots .$

3. $(1+x)^{-2}=1-2 x+3 x^{2}-4 x^{3}+5 x^{4}-\ldots .$

4. $(1-x)^{-2}=1+2 x+3 x^{2}+4 x^{3}+5 x^{4}+\ldots$

5. $(1+x)^{-3}=1-3 x+6 x^{2}-10 x^{3}+15 x^{4}-\ldots .$

6. $(1-x)^{-3}=1+3 x+6 x^{2}+10 x^{3}+15 x^{4}+\ldots$

7. $(1-x)^{-n}=1+{ }^{n} C_{1} x+{ }^{n+1} C_{2} x^{2}+{ }^{n+2} C_{3} x^{3}+\ldots$

where if $n$ is a natural number.

Matrices

The algebra of matrices

A matrix is a numerical array that is rectangular in shape. The numbers could be simple or complex. It could be written as 

$A = \left[ {\begin{array}{*{20}{c}}{{a_{11}}}&{{a_{12}}}& \cdots &{{a_{1n}}} \\{{a_{21}}}&{{a_{22}}}& \cdots &{{a_{2n}}} \\\vdots &{}&{}&{} \\{{a_{m1}}}&{{a_{m2}}}& \cdots &{{a_{mn}}}\end{array}} \right]$

or as $A = {\left( {{a_{ij}}} \right)_{m \times n}}$.

A matrix with $m$ rows and $n$ columns is known as a $m \times n$matrix, and its size (or dimension) is also known as $m \times n$. 

A matrix $A = {\left( {{a_{ij}}} \right)_{m \times n}}$ is said to be a

(i) square matrix $\quad$ if $m = n$

(ii) row matrix $\quad $ if $m = 1$

(iii) column matrix $\quad $ if $n = 1$

(iv) Null or zero matrix $\quad $ if ${a_{ij}} = 0\forall i$ and $j$

(v) diagonal matrix $\quad $ if $m = n$ and ${a_{ij}} = 0$

(vi) scalar matrix $\quad $ if $m = n$ and ${a_{ij}} = 0$ $\forall i \ne j$ and ${a_{ii}} = \lambda \forall i$

(vii) unit or identity matrix if $m = n$ and ${a_{ij}} = 0$ $\forall i \ne j$ and${a_{ii}} = 1\forall i$

(viii) upper triangular matrix if $m=n$ and $a_{i j}=0$ $\forall i>j$

(ix) lower triangular matrix if $m=n$ and $a_{i j}=0$$\forall i<j$

A matrix is said to be triangular if it is either lower or upper triangular matrix.

Matrices Addition: If and only if two matrices $A$ and $B$ are the same size, they can be added. When two matrices are the same size, addition is performed term by term. As an example, 

$\left[ {\begin{array}{*{20}{l}}a&b&c \\d&e&f\end{array}} \right] + \left[ {\begin{array}{*{20}{l}}p&q&r \\s&t&u\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}{a + p}&{b + q}&{c + r} \\{d + s}&{e + t}&{f + u}\end{array}} \right]$

Scalar Multiplication:  If $A$ is a matrix and $\alpha $ is a scalar, $\alpha A$ is the matrix formed by multiplying each element of$A$ by $\alpha $. As an example, 

$3\left[ {\begin{array}{*{20}{c}}1&{ - 2}&5 \\7&8&1\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}3&{ - 6}&{15} \\{21}&{24}&3\end{array}} \right]$

Properties of Scalar Multiplication:  If $A$ and $B$ are two matrices of the same size, and $\alpha ,\beta $ are two scalars, then 

$\begin{align}& (\alpha +\beta )A\text{ }=\alpha A+\beta A \\& (\alpha \beta )A\text{ }=\alpha (\beta A) \\& \alpha (A+B)\text{ }=\alpha A+\alpha B\text{ } \\\end{align}$

Matrix Multiplication: Let $A = {\left( {{a_{ij}}} \right)_{m \times n}}$ and $B = {\left( {{b_{ij}}} \right)_{r \times s}}$ be two matrices. We say that $A$ and $B$ are comparable for the product $AB$if $n = r$, that is, if the number of columns of $A$ is equal to the number of rows of $B$.

Properties of Matrix Multiplication

If $A = {\left( {{a_{ij}}} \right)_{m \times n}},B = {\left( {{b_{ij}}} \right)_{n \times p}}$ and $C = {\left( {{c_{ij}}} \right)_{p \times q}}$ then

1. $(AB)C = A(BC)$  [Associative law]

2. $A{I_n} = {I_m}A = A$

3. $AB$may not be equal to $BA$

4. $k(AB) = (kA)B = A(kB)$ where $k$ is a scalar

5. If $A$ is a square matrix, then

${A^m}{A^n} = {A^{m + n}}\forall m,n \in {\mathbf{N}}$

${\left( {{A^m}} \right)^n} = {A^{mn}}\quad \forall m,n \in {\mathbf{N}}.$

6. If $A$ is an invertible matrix then ${\left( {{A^{ - 1}}BA} \right)^m} = {A^{ - 1}}{B^m}A{\text{and }}{A^{ - m}} = {\left( {{A^{ - 1}}} \right)^m}\forall m \in {\mathbf{N}}.$

Transpose of a matrix

Assume $A = {\left( {{a_{ij}}} \right)_{m \times n}}$ is a matrix. The $A$ transpose, denoted by ${A^\prime }$or ${A^t}$, is the matrix ${A^\prime } = {\left( {{b_{ij}}} \right)_{n \times m}}$, where ${b_{ij}} = {a_{ji}}\forall i$ and $j$. 

By $\bar A$ we mean a matrix $B = {\left( {{b_{ij}}} \right)_{m \times n}}$ where ${b_{ij}} = {\bar a_{ij}}$ where $\bar a$ denotes the conjugate of $a$. 

By ${A^*}$ we mean

${A^*} = {(\bar A)^\prime } = \left( {{{\bar A}^\prime }} \right)$

Properties of Transpose of Matrix

1. ${(A + B)^\prime } = {A^\prime } + {B^\prime }$

2. ${(kA)^\prime }\quad  = k{A^\prime }$ where $k$ is a scalar

3. ${(AB)^\prime }\quad  = {B^\prime }{A^\prime }\quad $ [Reversal law]

4. If $A$ is an invertible matrix, then ${\left( {{A^{ - 1}}} \right)^\prime } = {\left( {{A^\prime }} \right)^{ - 1}}$

Minors and cofactors

Minor

Allow $A = {\left( {{a_{ij}}} \right)_{n \times n}}$ to be a square matrix of order n. The determinant of the square sub-matrix of order $(n - 1)$ obtained by deleting the ith row and $j$th column of matrix $A$ is then the minor ${M_{ij}}$ of the element ${a_{ij}}$ of matrix $A$. 

Cofactors

Let $A = {\left( {{a_{ij}}} \right)_{n \times n}}$ be a square matrix of order $n$. Then the cofactor of the element ${a_{ij}}$ of the matrix $A$ is denoted by ${C_{ij}}$ and is equal to ${( - 1)^{i + j}}{M_{ij}}$ where ${M_{ij}}$ is the minor of the element ${a_{ij}}$ of the matrix $A$.

Note that

$\left| {\begin{array}{*{20}{l}}{{a_{11}}}&{{a_{12}}}&{{a_{13}}} \\{{a_{21}}}&{{a_{22}}}&{{a_{23}}} \\{{a_{31}}}&{{a_{32}}}&{{a_{33}}}\end{array}} \right| = {a_{11}}{M_{11}} - {a_{12}}{M_{12}} + {a_{13}}{M_{13}} = {a_{11}}{C_{11}} + {a_{12}}{C_{12}} + {a_{13}}{C_{13}}$

Adjoint and inverse of the matrix

Let $A = {\left( {{a_{ij}}} \right)_{n \times n}}$ be the square matrix. The adjoint of $A$ is defined as the matrix $adjA = {\left( {{b_{ij}}} \right)_{n \times n}}$ where ${b_{ij}} = {A_{ji}}$ and ${A_{ji}}$ is the cofactor of the $(j,i)$th element of $A$. 

Properties of Adjoint

1. $A(\operatorname{adj} A) = (\operatorname{adj} A)A = |A|{I_n}$

2. $\operatorname{adj} (kA) = {k^{n - 1}}(\operatorname{adj} A)$

3. $\operatorname{adj} (AB) = (\operatorname{adj} B)(\operatorname{adj} A)$

Definition: A square matrix $A$ is said to be singular if $|A| = 0$ and non-singular if $|A| \ne 0$.

Definition: Inverse of a square matrix $A = {\left( {{a_{ij}}} \right)_{n \times n}}$ is the matrix $B = {\left( {{b_{ij}}} \right)_{n \times n}}$ such that

$AB = BA = {I_n}.$

In fact ${A^{ - 1}} = \dfrac{1}{{|A|}}(\operatorname{adj} A)$ if $|A| \ne 0\$ 

Properties of Inverse

Let $A$ and $B$ be two invertible matrices of the same size.

1. Inverse of a matrix if it exists is unique.

2. $A{A^{ - 1}} = {A^{ - 1}}A = {I_n}$

3. ${\left( {{A^{ - 1}}} \right)^{ - 1}} = A$

4. ${(kA)^{ - 1}} = {k^{ - 1}}{A^{ - 1}}$ if $k \ne 0$

5. ${(AB)^{ - 1}} = {B^{ - 1}}{A^{ - 1}}$

Special Type of Matrix: 

Symmetric matrix:  It is defined as the square matrix which is equal to its transpose

A square matrix $A = \left[ {{a_{ij}}} \right]$ is called symmetric matrix, if ${a_{ij}} = {a_{ji}}$ for all i, j or ${A^T} = A$

e.g.,

$\left[ {\begin{array}{*{20}{l}}a&h&g \\h&b&f \\g&f&c\end{array}} \right]$

Hence, it is a symmetric matrix.

Skew- symmetric matrix:  It is defined as a square matrix which is equal to the negative of its transpose. 

A square matrix $A = \left[ {{a_{ij}}} \right]$ is called skew-symmetric matrix, if ${a_{ij}} =  - {a_{ji}}$ for all $i,j$ or ${A^T} =  - A$.

$\left[ {\begin{array}{*{20}{c}}0&h&g \\{ - h}&0&f \\{ - g}&{ - f}&0\end{array}} \right]$

All principal diagonal elements of a skew-symmetric matrix are always zero because of any diagonal element.

${{a}_{ij}}=-{{a}_{ij}}$

For  i = j(i.e for diagonal elements)

$\Rightarrow {{a}_{ii}}=0$

Thus, it is a skew-symmetric matrix. 

Properties of Symmetric and Skew-symmetric Matrices

(i) If $A$ is a square matrix, then $A + {A^T},A{A^T},{A^T}A$ are symmetric matrices, while $A - {A^T}$ is skew-symmetric matrix.

(ii) If ${\text{A}},{\text{B}}$ are two symmetric matrices, then

(a) $A \pm B, AB + BA$ are also symmetric matrices,

(b) $AB - BA$ is a skew-symmetric matrix,

(c) $AB$ is a symmetric matrix, when $AB = BA$.

(iii) If $A,B$ are two skew-symmetric matrices, then

(a) $A \pm B,AB - BA$ are skew-symmetric matrices,

(b) $AB + BA$ is a symmetric matrix.

(iv) Every square matrix $A$ can uniquely be expressed as sum of a symmetric and skew-symmetric matrix

i.e., $A = \left[ {\dfrac{1}{2}\left( {A + {A^T}} \right)} \right] + \left[ {\dfrac{1}{2}\left( {A - {A^T}} \right)} \right]$.

Determinants

Evaluation of Determinants

A determinant of order two is written as

$\left| {\begin{array}{*{20}{l}}{{a_{11}}}&{{a_{12}}} \\{{a_{21}}}&{{a_{22}}}\end{array}} \right|\quad \left( {{a_{ij}} \in {\mathbf{C}}\forall i,j} \right)$

and is equal to ${a_{11}}{a_{22}} - {a_{12}}{a_{21}}$.

A determinant of order three is written as

$\left| {\begin{array}{*{20}{l}}{{a_{11}}}&{{a_{12}}} \\{{a_{21}}}&{{a_{22}}}\end{array}} \right|\quad \left( {{a_{ij}} \in {\mathbf{C}}\forall i,j} \right)$

and is equal to

\[ a_{11} \begin{vmatrix} a_{22} & a_{23} \\ a_{32} & a_{33} \\ \end{vmatrix} - a_{12} \begin{vmatrix} a_{21} & a_{23} \\ a_{31} & a_{33} \\ \end{vmatrix} + a_{13} \begin{vmatrix} a_{21} & a_{22} \\ a_{31} & a_{32} \\ \end{vmatrix} \]

$= {a_{11}}{a_{22}}{a_{33}} + {a_{12}}{a_{23}}{a_{31}} + {a_{13}}{a_{32}}{a_{21}} - {a_{13}}{a_{31}}{a_{22}} - {a_{32}}{a_{23}}{a_{11}} - {a_{12}}{a_{21}}{a_{33}}$

Properties of Determinants

1. Reflection Property

If the determinant's rows are changed into columns and the columns into rows, the determinant remains unchanged.

2. All-zero Property The determinant is zero if all of the elements in a row (column) are zero. 

3. Proportionality [Repetition] Property

If the elements of a row (column) are proportional, or if the elements of another row (column) are proportional, then the determinant is zero. 

4. Switching Property: The interchange of any two determinant rows (columns) changes its sign. 

5. Scalar Multiple Property: If all the elements of a determinant's row (column) are multiplied by a non-zero constant, the determinant is multiplied by the same constant. 

6. Property of Invariance

$\left| {\begin{array}{*{20}{l}}{{a_1}}&{{b_1}}&{{c_1}} \\{{a_2}}&{{b_2}}&{{c_2}} \\{{a_3}}&{{b_3}}&{{c_3}}\end{array}} \right| = \left| {\begin{array}{*{20}{l}}{{a_1} + \alpha {b_1} + \beta {c_1}}&{{b_1}}&{{c_1}} \\{{a_2} + \alpha {b_2} + \beta {c_2}}&{{b_2}}&{{c_2}} \\{{a_3} + \alpha {b_3} + \beta {c_3}}&{{b_3}}&{{c_3}}\end{array}} \right|$

So, a determinant remains unaltered under an operation of the form ${C_i} \to {C_i} + \alpha {C_j} + \beta {C_k}$, where $j,k \ne i$, or an operation of the form ${R_i} \to {R_i} + \alpha {R_j} + \beta {R_k}$, where $j$, $k \ne i$.

7. Sum Property

$\left| {\begin{array}{*{20}{l}}{{a_1} + {b_1}}&{{c_1}}&{{d_1}} \\{{a_2} + {b_2}}&{{c_2}}&{{d_2}} \\{{a_3} + {b_3}}&{{c_3}}&{{d_3}}\end{array}} \right| = \left| {\begin{array}{*{20}{c}}{{a_1}}&{{c_1}}&{{d_1}} \\{{a_2}}&{{c_2}}&{{d_2}} \\{{a_3}}&{{c_3}}&{{d_3}}\end{array}} \right| + \left| {\begin{array}{*{20}{c}}{{b_1}}&{{c_1}}&{{d_1}} \\{{b_2}}&{{c_2}}&{{d_2}} \\{{b_3}}&{{c_3}}&{{d_3}}\end{array}} \right|$

8. Factor Property: If a determinant $\Delta$ becomes zero when $x = \alpha $ is entered, then $(x - \alpha )$ is a factor of $\Delta$. 

9. Triangle Property: If all of a determinant's elements above or below the main diagonal are zeros, the determinant is equal to the product of diagonal elements. That is to say, 

$\left| {\begin{array}{*{20}{c}}{{a_1}}&{{a_2}}&{{a_3}} \\0&{{b_2}}&{{b_3}} \\0&0&{{c_3}}\end{array}} \right| = \left| {\begin{array}{*{20}{c}}{{a_1}}&0&0 \\{{a_2}}&{{b_2}}&0 \\{{a_3}}&{{b_3}}&{{c_3}}\end{array}} \right| = {a_1}{b_2}{c_3}$

Linear Equations

The system of linear homogeneous equations

${a_1}x + {b_1}y + {c_1}z = 0$

${a_2}x + {b_2}y + {c_2}z = 0$

${a_3}x + {b_3}y + {c_3}z = 0$ 

has a non-trivial solution (i.e., at least one of the $x,y,z$ is different from zero) if and only if $\Delta  = 0,$ where

$\Delta  = \left| {\begin{array}{*{20}{l}}{{a_1}}&{{b_1}}&{{c_1}} \\{{a_2}}&{{b_2}}&{{c_2}} \\{{a_3}}&{{b_3}}&{{c_3}}\end{array}} \right|$

If $\Delta  \ne 0$, then the only solution of the above system of equations is $x = 0,y = 0$ and $z = 0$.

Cramer's Rule

If $\Delta  = \left| {\begin{array}{*{20}{l}}{{a_1}}&{{b_1}}&{{c_1}}\\{{a_2}}&{{b_2}}&{{c_2}} \\{{a_3}}&{{b_3}}&{{c_3}}\end{array}} \right| \ne 0$ then the solution of the system of linear equations

${a_1}x + {b_1}y + {c_1}z = {d_1}$

${a_2}x + {b_2}y + {c_2}z = {d_2}$

${a_3}x + {b_3}y + {c_3}z = {d_3}$  is given by $x = \dfrac{{{\Delta _1}}}{\Delta },y = \dfrac{{{\Delta _2}}}{\Delta },z = \dfrac{{{\Delta _3}}}{\Delta }$

where

${\Delta _1} = \left| {\begin{array}{*{20}{l}}{{d_1}}&{{b_1}}&{{c_1}} \\{{d_2}}&{{b_2}}&{{c_2}} \\{{d_3}}&{{b_3}}&{{c_3}}\end{array}} \right|,{\Delta _2} = \left| {\begin{array}{*{20}{l}}{{a_1}}&{{d_1}}&{{c_1}} \\{{a_2}}&{{d_2}}&{{c_2}} \\{{a_3}}&{{d_3}}&{{c_3}}\end{array}} \right|$ and ${\Delta _3} = \left| {\begin{array}{*{20}{l}}{{a_1}}&{{b_1}}&{{d_1}} \\{{a_2}}&{{b_2}}&{{d_2}} \\{{a_3}}&{{b_3}}&{{d_3}}\end{array}} \right|$

Probability

Definitions

1. A random experiment is one in which all of the experiment's outcomes are known ahead of time, and (ii) the exact outcome of any specific performance of the experiment is unpredictable, i.e. not known ahead of time. 

2.  A sample space, denoted by $S,$associated with a random experiment is a set of points such that each element of $S,$ denotes an experiment outcome, and (ii) any experiment performance results in an outcome that corresponds to exactly one element of $S$. In other words, the sample space contains all of the possible outcomes of the random experiment.  The elements of the sample space associated with a random experiment are called the elementary or simple or indecomposable events of that experiment.

3.  A random experiment is associated with an event, which is a subset of the sample space $S$ (associated with that experiment). We say that an event $E$ ( $ \subseteq S$ ) has occurred if the experiment's outcome $\omega $ is an element of $E$. If the experiment's outcome $\omega $ is such that $\omega  \notin E$, we say that the event $E$did not occur. 

The empty set $\emptyset $, which is a subset of every set, also represents an event and is said to be an impossible event. The set $S$ is a subset of $S$ and represents the sure event.

Classical definition of Probability

If a random experiment produces $N$ mutually exclusive, equally likely, and exhaustive outcomes, of which $n$ are favourable to the occurrence of an event $A$, then the probability of occurrence of $A$ is given by $P(A)$. 

$P(A) = \dfrac{n}{N}$

A few theorems on probability

1. If $A$ and $B$ are two mutually exclusive events, then $P(A \cup B) = P(A) + P(B)$.

2. If $A$ is any event, then $P\left( {{A^\prime }} \right) = 1 - P(A)$

Here, P is the probability. Also, $P\left( {{A^\prime }} \right)$ is termed as a complement of P(A).

3. If $A$ and $B$ are two events, then

$P\left( {A \cap {B^\prime }} \right) = P(A) - P(A \cap B)$

4. If $A$ and $B$ are two events, then $P(A \cup B) = P(A) + P(B) - P(A \cap B)$

5. If $A$ and $B$ are two events, then $P$ (exactly one of $A,{\text{ }}B$ $occurs)$

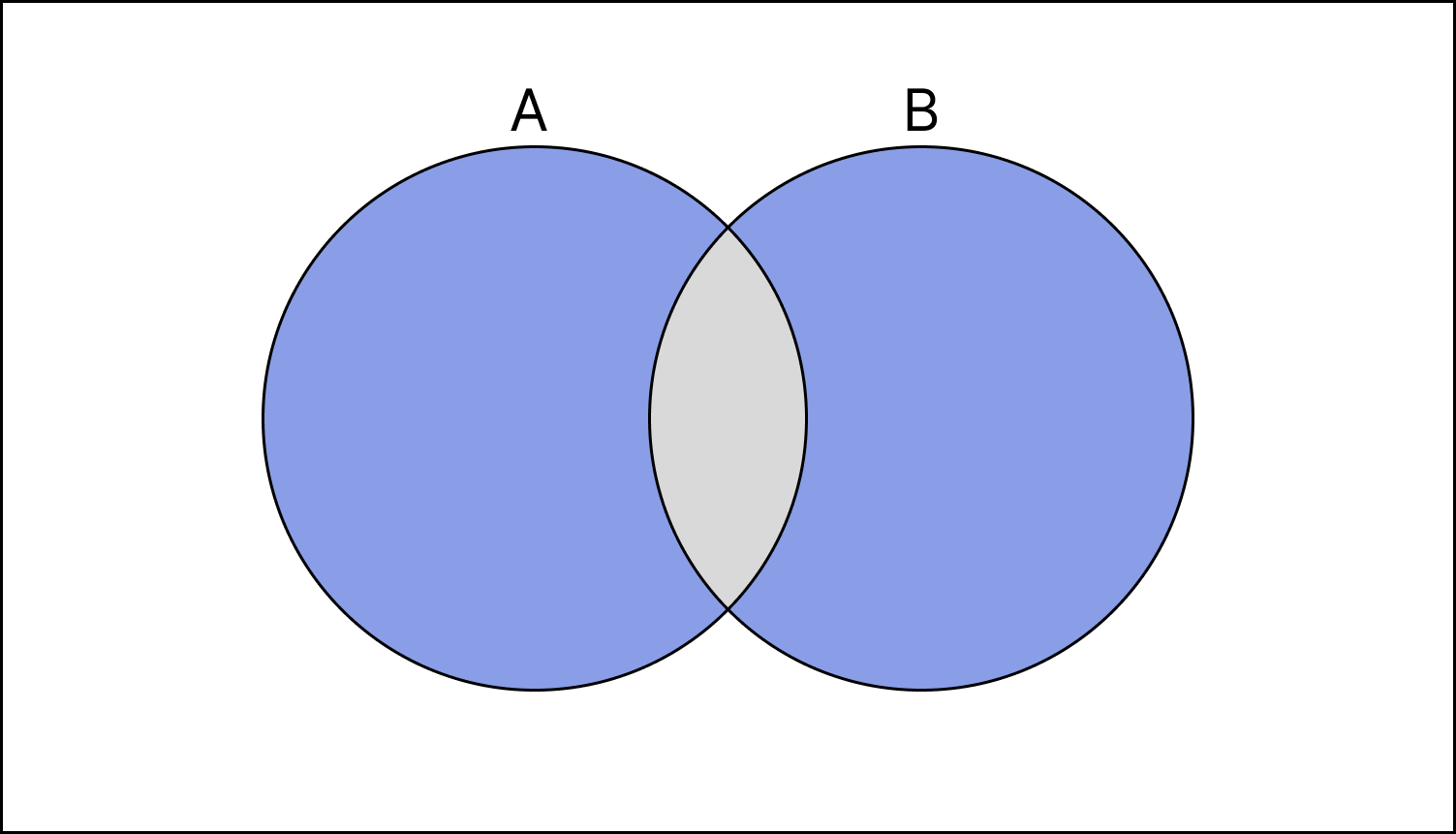
Event A and B

From figure,

$ = P\left[ {\left( {A \cap {B^\prime }} \right) \cup \left( {{A^\prime } \cap B} \right)} \right]$

$= P(A) - P(A \cap B) + P(B) - P(A \cap B)$

$ = P(A) + P(B) - 2P(A \cap B)$

$= P(A \cup B) - P(A \cap B){\text{ }}$

${\text{Also, }}P({\text{ exactly one of }}A,B{\text{ occurs }})$

$= P\left( {A \cap {B^\prime }} \right) + P\left( {{A^\prime } \cap B} \right)$

$= P\left( {{B^\prime }} \right) - P\left( {{A^\prime } \cap {B^\prime }} \right) + P\left( {{A^\prime }} \right) - P\left( {{A^\prime } \cap {B^\prime }} \right)$

$= P\left( {{A^\prime }} \right) + P\left( {{B^\prime }} \right) - 2P\left( {{A^\prime } \cap {B^\prime }} \right)$

$= P\left( {{A^\prime } \cup {B^\prime }} \right) - P\left( {{A^\prime } \cap {B^\prime }} \right)$

6. If $A$ and $B$ are two events

$P\left( {{A^\prime } \cup {B^\prime }} \right) = 1 - P(A \cap B\,\,{\kern 1pt} {\text{and }}P\left( {{A^\prime } \cap {B^\prime }} \right) = 1 - P(A \cup B)$

Independent Events

We say that two events $A$ and $B$ are independent if the occurrence or non-occurrence of  does not affect the probability of occurrence or non-occurrence of , that is, if  provided $P(A) \ne 0$

We say that two things happened. $A$ and $B$ are independent if the occurrence or non-occurrence of $A(B)$ has no effect on the probability of occurrence or non-occurrence of $B(A)$, that is, if $P(B\mid A) = P(B)$if  provided $P(A) \ne 0$

$\Rightarrow \dfrac{{P(B \cap A)}}{{P(A)}} = P(B) \Rightarrow P(A \cap B) = P(A)P(B)$

Thus, two events $A$ and $B$ are independent if and only if $P(A \cap B) = P(A)P(B)$

If two events are not independent, they are said to be dependent.

Mean and Variance of a Random Variable

The expectation (mean) of the random variable $X$ is defined as

$E(X) = \sum\limits_{i = 1}^n {{p_i}} {x_i}$ and the variance of $X$ is defined as $\operatorname{var} (X) = \sum\limits_{i = 1}^n {{p_i}} {\left( {{x_i} - E(X)} \right)^2} = \sum\limits_{i = 1}^n {{p_i}} x_i^2 - {(E(X))^2}$

Bayes Rule

Let $S$ be a sample space and $H_{1}, \cdots, H_{n}$ be $n$ mutually exclusive events such that $\bigcup_{j=1}^{n} H_{j}=S$ and $P\left(H_{j}\right)>0$ for $j=1,2, \cdots, n$. We can think of the $H_{j}$ 's as the 'causes' (or the hypotheses) that lead to the outcome of an experiment. The probabilities $P\left(H_{j}\right), j=1,2, \cdots, n$ are called prior probabilities. Suppose the experiment results in an outcome of event $A$, where $P(A)>0$. 

Bayes Theorem

Let $\left\{H_{j}\right\}$ be mutually exclusive events such that $P\left(H_{j}\right)>0$ for $j=1,2, \cdots, n$ and $S=\bigcup_{j=1}^{n} H_{j}$. Let $A$ be an event with $\mid P(A)>0 .$ Then for $j=1,2, \cdots, n$

$P\left(H_{j} \mid A\right)=\dfrac{P\left(H_{j}\right) P\left(A \mid H_{j}\right)}{\sum_{k=1}^{n} P\left(H_{k}\right) P\left(A \mid H_{k}\right)}$

Probability Distribution of a Random Variable

Description giving the values of the random variable along with the corresponding probab is called the probability distribution of the random variable $X$.

In general, the probability distribution of a random variable $X$ is defined as follows:

The probability distribution of a random variable $X$ is the system of numbers

$\mathrm{X}: x_{1}, x_{2}, \cdots  x_{n} $

$\mathrm{P}(\mathrm{X}) : p_{1}, p_{2}, \cdots, p_{n}$

where,

$p_{i}>0, \quad \sum_{i=1}^{n} p_{i}=1, i=1,2, \ldots, n$

The real numbers $x_{1}, x_{2}, \ldots, x_{n}$ are the possible values of the random variable $\mathrm{X}$ and $p_{\mathrm{i}}(i=1,2, \ldots, n)$ is the probability of the random variable $\mathrm{X}$ taking the value $x_{i}$ i.e., $\mathrm{P}\left(\mathrm{X}=x_{i}\right)=p_{i}$

Bernoulli Trials

• The outcome of any trial is independent of the outcome of any other trial. In such trials, the probability of success or failure remains constant. Such independent trials, which have only two outcomes, are usually referred to as 'success' or 'failure' are called Bernoulli trials.

• Trials of a random experiment are called-Bernoulli trials if they satisfy the following conditions:

There should be a finite number of trials.

• The trials should be independent.

• Each trial has exactly two outcomes: success or failure.

• The probability of success remains the same in each trial.

Example: 30 Six balls are drawn successively from an urn containing 7 red and 9 black balls. Tell whether or not the trials of drawing balls are Bernoulli trials when after each draw, the ball drawn is (i) replaced (ii) not replaced in the urn.

Solution

(i) The number of trials is finite. When the driving is done with replacement, the probability of success (say, red ball) is $\mathrm{P}=\dfrac{7}{16}$, which is same for all six trials (draws). Hence, the drawing of balls with replacements are Bernoulli trials.

(ii) When the drawing is done without replacement, the probability of success (i.e., red ball) in first trial is $\dfrac{7}{16}$, in 2nd trial is $\dfrac{6}{15}$ if the first ball drawn is red or $\dfrac{7}{15}$ if the first ball drawn is black and so on. Clearly, the probability of success is not the same for all trials. hence the trials are not Bernoulli trials

Importance of Maths Vector Algebra

When a physical quantity has magnitude and direction, it is called a vector quantity. Previously, we have learned how to calculate only the magnitude of different scalar quantities using simple algebraic formulas. In this chapter, the introduction of direction and magnitude will alter the formulas and their relevant operations in a certain way.

Students will learn how to derive formulas related to vector mathematics and apply them to calculate the answers to the related questions. This chapter covers the multiplication of vector quantities and the determination of the outcomes.

All the formulas are derived and explained using algebraic operations. This chapter is very important for JEE aspirants to score well in the exam.

Here, students will learn a significant difference between vector algebra and algebra. The outcomes are different but can be comprehended easily when you choose to follow the revision notes for Algebra for JEE Advanced prepared by our subject experts at Vedantu.

It is a fundamental chapter as the concepts will be used in studying advanced concepts of Physics and Mathematics. Hence, prepare this chapter well to ensure a strong foundation of these concepts.

Benefits of Algebra JEE Advanced Notes PDF

• These revision notes are designed by the subject matter experts in an easy manner. It will help students to revise the concepts of algebra faster and better. These notes provide an easier explanation of all formulas and their derivations. Also, the terms involved in the formulas are explained properly in these notes.

• The concise format of the revision notes will enable you to learn this chapter in no time. So by using these notes for revising this chapter before your exam, you will be able to revise the concepts faster.

• These revision notes help you to assess your understanding of the concepts as well. After completing this chapter, solve the sample Algebra JEE Advanced revision questions and find out the solutions provided by the experts. Check and compare your answers with the solutions provided by the experts and evaluate your preparation.

Download Algebra JEE Advanced Revision Notes Free PDF

Students can get the free PDF of these revision notes from Vedantu to prepare the chapter on vector algebra. The simpler explanations of concepts provided in these notes definitely help them to revise the chapter faster. They can find out the implication of the vector algebra formulas and develop a strong conceptual foundation for this chapter with the help of these notes. Therefore, these Algebra JEE Advanced revision notes are imperative for effective exam preparation.

Important Related Links for JEE Main and JEE Advanced