Question

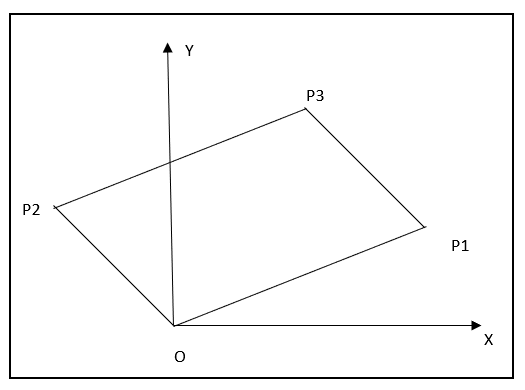
If the points ${{P}_{1}}$ and ${{P}_{2}}$ represent two complex numbers ${{z}_{1}}$ and ${{z}_{2}}$, then the point ${{P}_{3}}$ represents

A. ${{z}_{1}}+{{z}_{2}}$
B. ${{z}_{1}}-{{z}_{2}}$
C. ${{z}_{1}}\times {{z}_{2}}$
D. ${{z}_{1}}\div {{z}_{2}}$

Answer 1

Hint: In this question, we have to find the complex number at point ${{P}_{3}}$. For this, the property of parallelogram i.e., the midpoints of the diagonals of a parallelogram are equal is used.

Formula Used: The complex number $(x,y)$ is represented by $x+iy$.
If $z=x+iy\in C$, then $x$ is called the real part and $y$ is called the imaginary part of $z$. These are represented by $\operatorname{Re}(z)$ and $\operatorname{Im}(z)$ respectively.
$z=x+iy$ be a complex number such that $\left| z \right|=r$ and $\theta $ be the amplitude of $z$. So, $\cos \theta =\dfrac{x}{r},\sin \theta =\dfrac{b}{r}$
And we can write the magnitude as
 $\begin{align}
  & \left| z \right|=\left| x+iy \right| \\
 & \Rightarrow r=\sqrt{{{x}^{2}}+{{y}^{2}}} \\
\end{align}$
Thus, we can write
$z=x+iy=r\cos \theta +ir\sin \theta =r(\cos \theta +i\sin \theta )$
This is said to be the mod amplitude form or the polar form of $z$.
Where $\cos \theta +i\sin \theta $ is denoted by $cis\theta $ and the Euler’s formula is $\cos \theta +i\sin \theta ={{e}^{i\theta }}$

Complete step by step solution: Given that,
The points ${{P}_{1}}$ and ${{P}_{2}}$ are represented by the complex numbers ${{z}_{1}}$ and ${{z}_{2}}$.
These are the vertices of the given parallelogram $O{{P}_{1}}{{P}_{2}}{{P}_{3}}$
So, the midpoints of its diagonals are equal. I.e.,
${{P}_{1}}{{P}_{2}}=O{{P}_{3}}$
The midpoint of ${{P}_{1}}{{P}_{2}}$ is
$\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)\text{ }...(1)$
The midpoint of $O{{P}_{3}}$ is
$\left( \dfrac{0+x}{2},\dfrac{0+y}{2} \right)\text{ }...(2)$
On equating (1) and (2), we get
\[{{P}_{3}}(x,y)=({{x}_{1}}+{{x}_{2}},{{y}_{1}}+{{y}_{2}})\]
Thus, this point is represented in the complex form as
$\begin{align}
  & ({{x}_{1}}+{{x}_{2}},{{y}_{1}}+{{y}_{2}})=({{x}_{1}}+{{x}_{2}})+i({{y}_{1}}+{{y}_{2}}) \\
 & \Rightarrow ({{x}_{1}}+i{{y}_{1}})+({{x}_{2}}+i{{y}_{2}}) \\
 & \Rightarrow {{z}_{1}}+{{z}_{2}} \\
\end{align}$
Thus, the point ${{P}_{3}}$ is represented by ${{z}_{1}}+{{z}_{2}}$.

Option ‘A’ is correct

Note: Here we need to remember that, the required point is one of the vertices of the given parallelogram. So, the property of the parallelogram is applied to find the required vertex.