Question

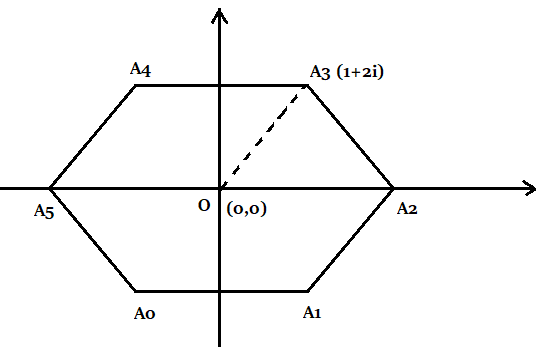
If centre of a regular hexagon is at origin and one of the vertexes on argand diagram is $1 + 2{\rm{i}}$ then its perimeter is
A. $2\sqrt 5$
B. $6\sqrt 2$
C. $4\sqrt 5$
D. $6\sqrt 5$

Answer 1

Hint: InIn our case, we are provided the information that we have to assume that centre of a regular hexagon is at origin and one of the vertexes on argand diagram is 1 + 2{\rm{i}} and we are to determine the perimeter of the regular hexagon. For that, we have to we have to use the Pythagoras theorem to determine the radial distance between origin to vertex and also perimeter formula of regular hexagon to determine the desired answer.

Formula Used: The regular hexagon’s perimeter can be calculated using the formula
$P = S \times 6$
Here, S is equal to the measurement of one side.

Complete step by step solution: Considering that the origin is at the centre of a regular hexagon and one of the vertices on argand dig,
$\left( {1 + 2i} \right)$

We have been already known that,
Six equilateral triangles form a regular hexagon.
As a result, the distance between the centre and any vertex is equal to the length of an external side.
The centre is loaded at $\left( {0,0} \right)$ and the vertex is loaded at
$\left( {1,2} \right)$
The Pythagorean Theorem can be used to calculate the radial distance from the origin to the vertex:
$ \Rightarrow r = \sqrt {{1^2} + {2^{2}}}$
On solving the terms inside the root, we get
$ \Rightarrow r = \sqrt 5 $
As we know that,
Six equal sides make up a regular hexagon.
Therefore, here each side length in this figure is
$\sqrt 5$
As we aware that the formula for a regular hexagon's perimeter is
$P = S \times 6$ ---- (1)
Here, S is equal to the measurement of one side.
The measurement of one side is found as,
$\sqrt 5$
Now, we have to substitute the value on the formula
$P = S \times 6$
Therefore, we get
 $= 6\sqrt 5$
Therefore, in a regular hexagon if one of the vertexes on argand diagram is 1 + 2{\rm{i}} then its perimeter is
$6\sqrt 5$ Units

Option ‘D’ is correct
Note: Student should be careful while soling this type of problem because; it includes some formulas to be remembered correctly. So, one should be very cautious in applying formulas as there are many types of hexagon, formulas might be confusable. And in order to get the desired solution we should apply the exact perimeter formula of regular hexagon.