Question

If \[A\] and $B$ are two sets, then $(A-B)\cup (B-A)\cup (A\cap B)$ is equal to
A. Only \[A\].
B. \[A\cup B\]
C. \[\left( A\cup B' \right)\]
D. None of these.

Answer 1

Hint: The union of two sets like $A\cup B$ which is read as “ $A$ union $B$” can be defined as the set of all the elements present in set $A$ and in set $B$whereas the intersection of two sets like $A\cap B$ which is read as “ $A$ intersection $B$” can be defined as the set of all the elements which is common in both set $A$ and in set $B$. $A-B$ is a set which contains all the elements that are present in set $A$ but not in set $B$.
So to solve this question we will first make the Venn diagrams of $A-B,\,B-A$and $A\cap B$. Then we will use union of all the three sets that is$(A-B)\cup (B-A)\cup (A\cap B)$ in the Venn diagram and determine from the shaded portion that $(A-B)\cup (B-A)\cup (A\cap B)$is equal to which of the options given.

Complete step by step solution: We are given two sets \[A\] and $B$ and we have to find the value of $(A-B)\cup (B-A)\cup (A\cap B)$ .

First we will make the Venn diagram of $A-B$.



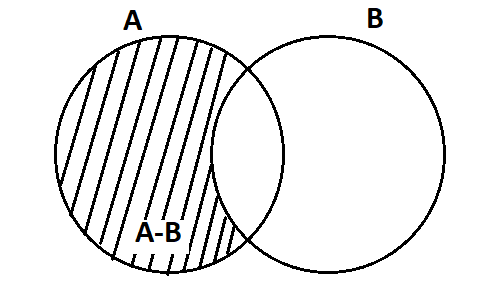
Now we will make the Venn diagram of $B-A$.

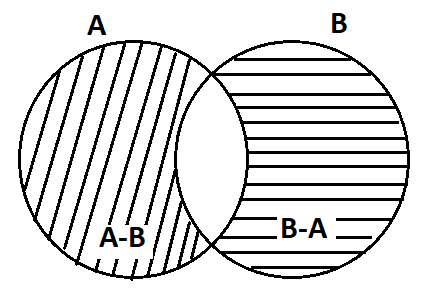
Now we will make the Venn diagram of $A\cap B$.



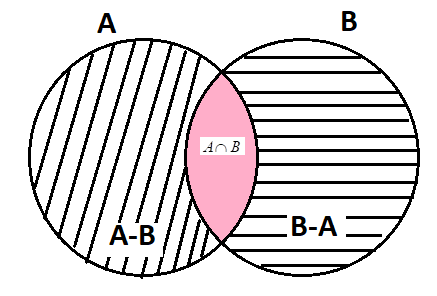
We will now use union in all the three sets $A-B,\,B-A$and $A\cap B$ that is $(A-B)\cup (B-A)\cup (A\cap B)$.

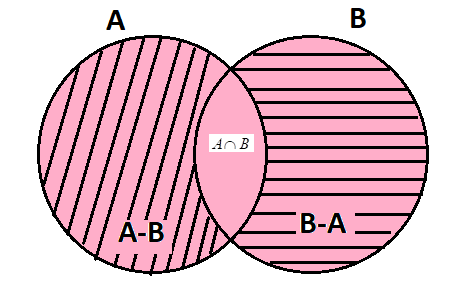
It means that $(A-B)\cup (B-A)\cup (A\cap B)$ will contain all the elements present in all the three sets $A-B,\,B-A$and $A\cap B$. And as $A-B,\,B-A$and $A\cap B$ has all elements from the set \[A\] and $B$then it means $(A-B)\cup (B-A)\cup (A\cap B)$ will contain all the elements of set \[A\] and $B$ that is \[A\cup B\]. Therefore $(A-B)\cup (B-A)\cup (A\cap B)$ is equals to \[A\cup B\].
If \[A\] and $B$ are two sets, then $(A-B)\cup (B-A)\cup (A\cap B)$ is equal to \[A\cup B\]
Option ‘B’ is correct

Note: We can also solve this question without using Venn diagram. L
$A-B$ will contain all the elements that are present in set $A$ but not in set $B$ and $B-A$ will contain all the elements present in set $B$ but not in set $A$.
So union of both $A-B$ and $B-A$ that is $(A-B)\cup (B-A)$ will have only those elements which are only present in set $A$ and set $B$ but are not common in both.
Now $A\cap B$ will contain all elements that is common in both set. Now union of $(A-B)\cup (B-A)\cup (A\cap B)$ will be,
$(A-B)\cup (B-A)\cup (A\cap B)=$Only $A\cup $ only $B\cup $ Common in both x and .
                                                      $=A\cup B$