Understanding Straight Lines and Circles in Geometry

Straight lines and circles are fundamental geometric constructs in coordinate geometry and complex number geometry, forming the basis for various advanced results and exam-level problem solving.

Coordinate and Complex Forms of the Straight Line

Definition: A straight line in the coordinate plane is the locus of points satisfying a linear equation, typically written as $ax + by + c = 0$, where $a$, $b$, $c$ are real constants and $(a, b) \neq (0, 0)$.

The primary forms of the straight line in the Cartesian plane include:

• Point–Slope form
• Two–Point form
• Slope–Intercept form
• Intercept form
• Normal form

Given a fixed point $A(x_1, y_1)$ and slope $m$, the point–slope form is $y - y_1 = m(x - x_1)$.

For points $A(x_1, y_1)$ and $B(x_2, y_2)$, the two–point form is $y-y_1 = \dfrac{y_2-y_1}{x_2-x_1}(x-x_1)$, valid if $x_1 \neq x_2$.

The slope–intercept form, for slope $m$ and $y$-intercept $c$, is $y = mx + c$.

The intercept form, for intercepts $a$ (on $x$-axis) and $b$ (on $y$-axis), is $\dfrac{x}{a} + \dfrac{y}{b} = 1$, provided $a, b \ne 0$.

Straight Lines Overview

Equations of Straight Lines in the Complex Plane

Let $z = x + iy$ represent a variable point and $z_0 = x_0 + i y_0$ be fixed. The general equation $ax + by + c = 0$ can be rewritten in complex notation. Recalling $x = \dfrac{z + \overline{z}}{2}$ and $y = \dfrac{z - \overline{z}}{2i}$, substituting yields the complex form:

$a \frac{z + \overline{z}}{2} + b \frac{z - \overline{z}}{2i} + c = 0$

Multiplying both sides by 2, and simplifying using $i^2 = -1$, gives:

$(a - ib)z + (a + ib)\overline{z} + 2c = 0$

Result: The general straight line in the complex plane has the form $\alpha z + \overline{\alpha}\,\overline{z} + k = 0$, where $\alpha$ is complex and $k$ real, $\alpha \ne 0$.

The slope in the complex representation is $-\dfrac{\overline{\alpha}}{\alpha}$.

Parametric Representation and Line Segment Division

The straight line through $z_1$ and $z_2$ in the complex plane is parametrically $z = (1-t)z_1 + t z_2$, where $t \in \mathbb{R}$. Every point on the line can be generated as $t$ varies, and the point dividing the segment $z_1 z_2$ in the ratio $m:n$ is $z = \frac{m z_2 + n z_1}{m + n}$.

For the locus equidistant from two points $p$, $q$ in the complex plane, $\lvert z - p \rvert = \lvert z - q \rvert$ gives the perpendicular bisector of the segment $pq$.

Conditions for Parallelism and Perpendicularity of Lines

Let $w_1$ and $w_2$ denote the slopes of two lines. Result: The lines are parallel if $w_1 = w_2$, and perpendicular if $w_1 w_2 = -1$ in the Cartesian plane. In the complex plane, associate slopes $w_1 = \dfrac{z_1 - z_2}{\overline{z_1} - \overline{z_2}}$ and $w_2 = \dfrac{z_3 - z_4}{\overline{z_3} - \overline{z_4}}$.

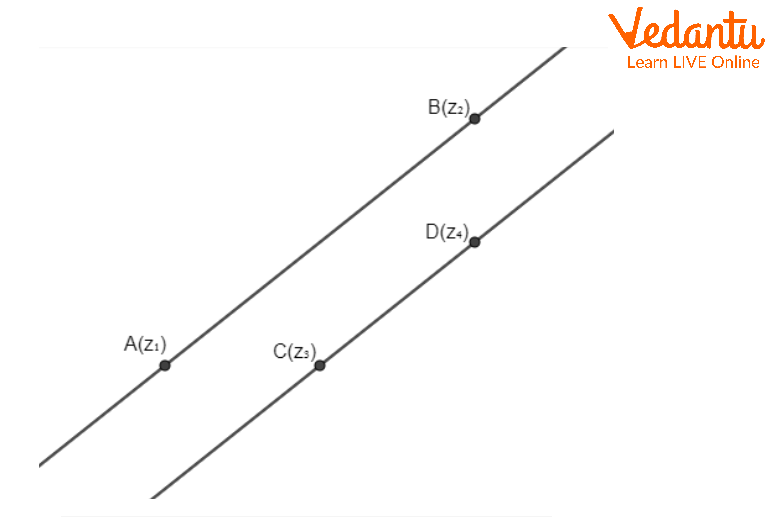
Parallelism: $w_1 = w_2$. For perpendicularity: $w_1 + w_2 = 0$. The arguments of the segments confirm these conditions, with $\operatorname{Arg}\left(\frac{z_1 - z_2}{z_3 - z_4}\right) = 0,\pi$ for parallel and $\pm \frac{\pi}{2}$ for perpendicular cases.

A misconception is to equate the complex slopes directly with real number slopes without considering the chosen orientation in the complex plane.

Geometry Of Complex Numbers

General Equations of the Circle in Cartesian and Complex Planes

A circle on the Cartesian plane with centre $(h, k)$ and radius $r$ has equation $(x-h)^2 + (y-k)^2 = r^2$.

The general form is $x^2 + y^2 + 2g x + 2f y + c = 0$, with centre $(-g, -f)$ and radius $\sqrt{g^2 + f^2 - c}$, provided $g^2 + f^2 - c > 0$.

Given endpoints $(a,b), (c,d)$ of a diameter, the equation is $(x-a)(x-c) + (y-b)(y-d) = 0$.

In the complex plane, for centre $z_0$ and radius $r$, the locus $\lvert z - z_0 \rvert = r$ forms the circle. Expanding, $\lvert z - z_0 \rvert^2 = (z - z_0)(\overline{z} - \overline{z_0}) = r^2$, which gives the general quadratic form in $z$ and $\overline{z}$.

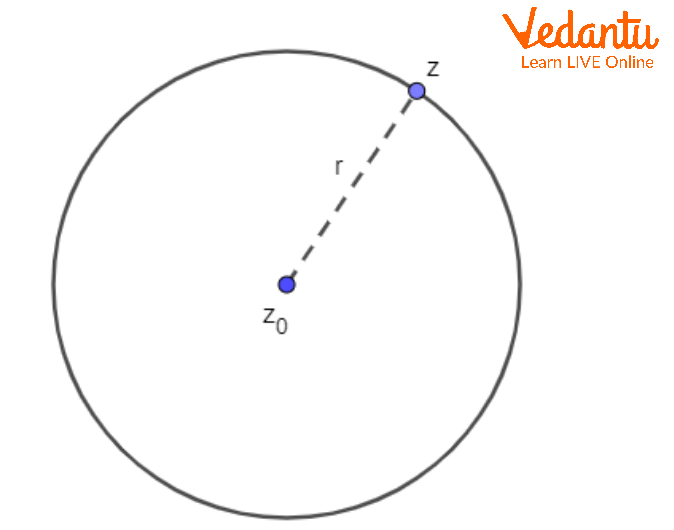
Identity: The general circle through complex geometry is $z\overline{z} + \overline{\alpha}\,z + \alpha\,\overline{z} + k = 0$, with centre $-\alpha$ and radius $\sqrt{|\alpha|^2 - k}$ when $|\alpha|^2 - k > 0$.

Straight Lines And Circles

Typical JEE Patterns on Straight Lines and Circles

Standard question types include finding intersection points, tangent and normal equations, loci derived from construction or transformation, and recognition of geometric relationships such as concurrency, orthogonality, and collinearity. Problems also frequently test conversion between the complex and Cartesian representations under exam constraints.

Properties And Solutions Of Triangles

Worked Examples Involving Core Results

Example: Find the equation of the line passing through $(1,2)$ with slope $-3$.

Substitute into point–slope form: $y-2 = -3(x-1)$.

Rearrange: $y = -3x + 5$.

Example: Determine the centre and radius of $x^2 + y^2 - 4x + 6y - 12 = 0$.

Rewrite: $x^2-4x + y^2+6y = 12$.

Complete the squares: $(x-2)^2 + (y+3)^2 = 25$.

Centre: $(2,-3)$, radius: $5$.

Example: Express the equation $3x - 2y + 7 = 0$ as a line in the complex plane.

$a = 3, b = -2$, so $\alpha = 3 + 2i$, $k = 7$. The complex line equation is $(3 - 2i)z + (3 + 2i)\overline{z} + 14 = 0$.

Example: For which values of $c$ does $x^2 + y^2 + c = 0$ represent a real circle?

Radius squared is $-c$. Hence, $-c > 0 \implies c < 0$.

Graphs Of Sine And Cosine Function

Interpretation of the Circle and Line in Problem Contexts

When a locus is constrained by equal distances, the resulting equation is of the form $\lvert z - p \rvert = \lvert z - q \rvert$, the perpendicular bisector. When a fixed distance from a point is specified, the locus forms a circle.

A frequent error is omitting the check for the trivial case $g^2 + f^2 - c > 0$ for the existence of a real circle in $x^2 + y^2 + 2gx + 2fy + c = 0$.

Functions And Its Types