Chemical Kinetics JEE Advanced 2026 Notes for Revision [Free PDF Download]
Chemical Kinetics is a crucial chapter in physical chemistry taught at the higher secondary level in the science stream. It is also an important chapter to study for JEE Advanced preparation. Students will learn the extent of a chemical reaction in this chapter and understand how a reaction propagates in a particular direction. They will learn how to calculate the rate of a chemical reaction using the explanation of various scientific principles. So download and refer to the Chemical Kinetics JEE Advance notes prepared by the subject experts of Vedantu to learn and revise these fundamental concepts.
Category: | JEE Advanced Revision Notes |
Content-Type: | Text, Images, Videos and PDF |
Exam: | JEE Advanced |
Chapter Name: | Chemical Kinetics |
Academic Session: | 2026 |
Medium: | English Medium |
Subject: | Chemistry |
Available Material: | Chapter-wise Revision Notes with PDF |
These revision notes have been compiled by our subject experts as per the updated JEE Advanced syllabus. Referring to these notes will help you comprehend the concepts easily.
JEE Advanced Revision Notes Chemistry Chemical Kinetics
When a chemical reaction is in progress, the concentration of the reactants decreases and the concentration of the products increases with the progress of time.
There is a change in the macroscopic properties (detectable properties like colour, concentration etc.,) of the system during a reaction.
The rate of reaction is defined as the decrease in the concentration of the reactants or the increase in the concentration of the product in a unit of time.
The unit of rate of a reaction is: \[{\text{mole li}}{{\text{t}}^{{\text{ - 1}}}}{{\text{s}}^{{\text{ - 1}}}}\]. In gaseous reaction the unit of rate of reaction are: ${\text{atm }}{{\text{s}}^{{\text{ - 1}}}}$
The rate of reaction generally decreases non uniformly as time proceeds.
For a reaction $A \to B$
The rate in terms of the concentration of reactant $A = \dfrac{{ - d\left[ A \right]}}{{dt}}$
The rate in terms of the concentration of product $B = \dfrac{{ + d\left[ B \right]}}{{dt}}$
In the reaction ${N_2} + 3{H_2} \to 2N{H_3},$the rate is equal to $\dfrac{{ - d\left[ {{N_2}} \right]}}{{dt}} = - \dfrac{1}{3}\dfrac{{ - d\left[ {{H_2}} \right]}}{{dt}} = + \dfrac{1}{2}\dfrac{{d\left[ {N{H_3}} \right]}}{{dt}}$
The slope of the tangent of the concentration-time curve at any point gives the rate of the reaction at that time.
The rate of reaction depends upon the nature of the reactants.
Ionic substance in an aqueous solution contains free ions. These ions can directly participate in reactions and those reactions are very fast or instantaneous.
Reactions between covalent substances are slow because in such reactions breaking of old bonds and formation of new covalent bonds occurs.
With an increase in the concentration of the reactants. the rate of the reaction increases (except for zero-order reactions ).
According to the law of mass action, rate = k$\left[Reactant\right]$n, where k is rate constant or specific rate and n is the order of the reaction.
With an increase in temperature, the rate of a reaction always increases, whether the reaction is exothermic or endothermic.
A catalyst increases the rate of reaction by carrying the reaction in a new path involving lower activation energy.
A catalyst alters the rate of reaction, the path of reaction, activation energy, threshold energy and rate constant.
Catalyst does not alter $\Delta H,\Delta S,\Delta G$ of reaction, the energy of reactants and the energy of products.
A catalyst favours both forward and backward reactions equally. Hence it does not affect the equilibrium constant.
For a chemical reaction to take place collisions between the reacting molecules are essential.
Only a fraction of the total number of collisions leads to a reaction. This fraction is known as effective or fruitful collisions.
Threshold Energy: The minimum energy which the molecules should possess so that their collisions lead to chemical reaction is called threshold energy.
The minimum extra energy which the molecules should possess, over and above the average energy, to enable them to react is called the energy of activation.
The greater the energy of activation of a reaction the lesser will be the rate constant and also the rate of the reaction.
The lesser the energy of activation of a reaction the higher will be the rate constant and also the rate of the reaction.
Molecules possessing the threshold energy are called activated in molecules. When activated molecules collide. An activated complex or a transition state is formed which changes into the products.
The energy of the activated complex is greater than the energy of the reactants and also the energy of the products.
The fraction of molecules which possess the energy of activation is given by the Boltzmann factor, ${e^{ - Ea/RT}}$.
With an increase in concentration, the number of activated molecules increases. Then a number of effective collisions increases due to which the rate of the reaction increases.
Heat of reaction $\Delta E = {\left( {Ea} \right)_f} - {\left( {Ea} \right)_b},$ where ${\left( {Ea} \right)_f}$is the energy of activation of the forward reaction and ${\left( {Ea} \right)_b}$is the energy of activation of the backward reaction.
In an exothermic reaction, the energy of activation of the backward reaction is greater than the energy of activation of the forward reaction.
In an endothermic reaction, the energy of activation of the backward reaction is lesser than the energy of activation of the forward reaction.
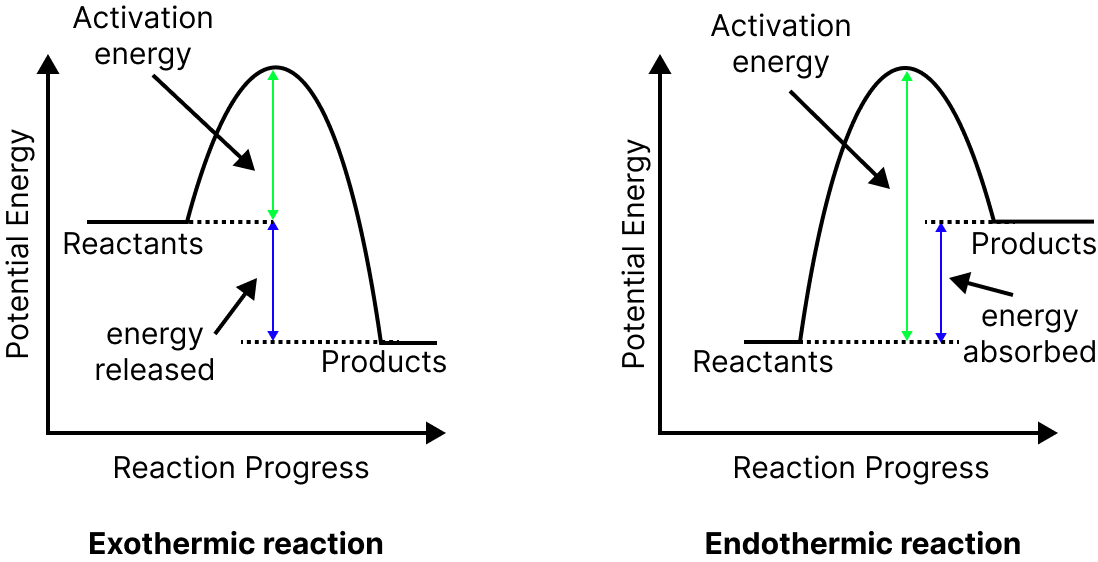
Image: Energy level diagrams of exothermic and endothermic reactions.
The relationship between the rate constant of a reaction and temperature is given by the Arrhenius equation.
$k = A.{e^{ - \dfrac{{{E_a}}}{{RT}}}}$, where ‘A’ is frequency factor.
When a graph is drawn between log K and I/T, a straight line (linear) is obtained with a negative slope.
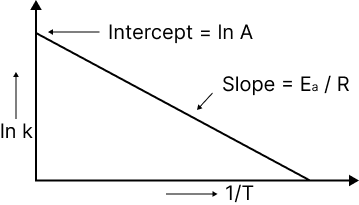
Image: A plot of In k and inverse of temperature
At two temperature T1 and T2, the rates constants K1 and K2 are given by :\[{\text{log}}\dfrac{{{{\text{k}}_{\text{2}}}}}{{{{\text{k}}_{\text{1}}}}}{\text{ = }}\dfrac{{{{\text{E}}{\text{a}}}}}{{{\text{2}}{\text{.303R}}}}\left[ {\dfrac{{{{\text{T}}_{\text{2}}}{\text{ - }}{{\text{T}}_{\text{1}}}}}{{{{\text{T}}_{\text{1}}}{{\text{T}}_{\text{2}}}}}} \right]\]
The mathematical dependence of the rate of a reaction on the molar concentration of the reaction is called the rate law or rate equation.
For a reaction, $aA + bB \to cC + dD,$rate$ = K{\left[ A \right]^x}{\left[ B \right]^y}$, where K is rate constant or specific rate, x is order of reaction with respect to A and y is order of reaction with respect to B.
The rate constant of a reaction becomes equal to the rate of the reaction when the concentration of all the reactants is unit.
Hence the rate constant is also known as the specific reaction rate.
Rate constant does not change with the change of concentration of reactants, products, volume of the vessel, and coefficients of reactants
The rate constant of a reaction is always a characteristic value at a given temperature.
The units of the rate constant of nth order reaction are: $li{t^{\left( {n - 1} \right)}}mol{e^{\left( {1 - n} \right)}}{\sec ^{ - 1}}$
The ratio between the rate constants of a reaction at two temperatures which differ by 10° is called the temperature coefficient of the reaction
For most of the reactions, the value of the temperature coefficient was found to be 2 to 3. This means that the rate constant of a reaction increases by 100 to 200% with 10℃ raises in temperature.
The slowest of different steps in the reaction mechanism is called rate limiting or rate-determining step of a reaction.
The number of chemical entities taking part in an elementary reaction, which collide with each other simultaneously in order to bring about a chemical reaction is termed molecularity of a reaction.
Molecularity may be 1 or 2 or, it can be neither zero nor fractional
The sum of the power of the concentration terms of the reactants in the rate equation of the reaction is known as the order of the reaction
The rate equation is determined experimentally from which we can know the order of the reaction. Rate is independent of the concentration of a reactant in a zero-order reaction.
For a zero-order reaction, rate is equal to the rate constant.
Units of rate constant are: ${\text{mol }}{{\text{L}}^{{\text{ - 1}}}}{{\text{s}}^{{\text{ - 1}}}}$
Rate is dependent on single concentration term in a first order reaction, rate = k x Concentration
Units of rate constant are: ${s^{ - 1}}$
Rate is dependent on two concentration terms in a second order ration, rate = $k \times {\left( {Concentration} \right)^2}$
Units of rate constant are: $Lmo{l^{ - 1}}{s^{ - 1}}$
If 'a' is initial concentration of the reactant, reduced to $\left( {a - x} \right)$in time t, the rate constant of a first order reaction, $k = \dfrac{{2.303}}{l}\log \dfrac{a}{{a - x}}$
Time taken for 50% completion of a reaction is called half- life $\left( {{t_{1/2}}} \right)$.
Half-life of a first order reaction is independent on the initial concentration, ${t_{1/2}} = \dfrac{{0.693}}{k}$
The time required for 75% completion of a first-order reaction is 2 half-lives, 87.5% completion is 3 half-lives and 99.9% completion is 10 half-lives.
Determination of Order of Reaction(n):
The order of the reaction is experimentally determined by the integrated equation method, Half-life method, Van’t Hoff differential method and Ostwald’s isolation method.
Integrated Equation Method: The various data is substituted into an integrated rate equation for different order of reactions. The rate equation which gives almost constant k decides the value of n.
Half-Life Method: Two half life time and corresponding concentrations are noted and used to calculate the n. The relationship between two half life is, $\dfrac{(t_{1/2})_1}{(t_{1/2})_2}=\left(\dfrac{([A_o])_2}{([A_o])_1}\right)^{n-1}$
Van’t Hoff Differential Method : In this method, order of reaction wrt each reactant is calculated by changing concentration of one reactant and keeping constant concentration of reactants.
Ostwald’s Isolation Method: This method is based on pseudo-alpha order which means that concentration terms of reactants except one if present in excess remain virtually unchanged and thus can be merged with rate constant. In this case, the order of reaction will be the same as the order wrt reactant which was not in excess. Similarly, order of reaction for all reacting species can be calculated.
Temperature dependence of rate constant (Arrhenius equation): Temperature Dependence of Rate Constant (Arrhenius Equation)" within the "Chemical Kinetics" chapter involves understanding how temperature impacts the rate of a chemical reaction. The Arrhenius Equation provides a mathematical framework for this relationship, revealing the sensitivity of reaction speed to temperature changes. It's akin to adjusting a control mechanism for reaction rates.
Importance of Physical Chemistry Chemical Kinetics
Chemical kinetics is all about calculating the rate of chemical reactions and finding out the products using proper scientific principles. In this chapter, you will study how the chemical reactions attain equilibrium and how the products are formed. It will also teach you how to determine the rate of a reaction over a long period and for an infinitesimal time period.
This chapter will also explain how to determine the order of a reaction and how to calculate those using different proven scientific techniques. All the terms relevant to the reaction kinetics will be explained to help you understand the fundamental concepts and determine the order of reactions.
The chapter will proceed to describe the molecularity of a reaction. It explains how many molecules are taking part in a chemical reaction in every elementary step. It will proceed to explain the integrated and differential rate laws using various mathematical techniques.
This chapter is crucial for you JEE Advanced preparation. The concepts teach us about a chemical reaction and enables us to calculate its rate. These concepts will be used in the other chapters of chemistry and during studying engineering in various streams. You will also be able to answer JEE Advanced questions on Chemical Kinetics without any difficulty when you go through these revision notes.
Benefits of Vedantu’s Chemical Kinetics JEE Notes PDF
The revision notes have been prepared by the experts as per the JEE Advanced syllabus. They have provided simpler descriptions to explain all the fundamental principles of this chapter for your easy understanding.
It will take less time to revise this chapter when you refer to the Chemical Kinetics IIT JEE notes. So save your precious time before the exam by studying the definitions, derivations, descriptions, and references given in these notes.
With the help of these notes you can learn many important tips to score well in the JEE exams.
Download Chemical Kinetics JEE Advance Notes Free PDF
Download the free PDF for a comprehensive revision of Chemical Kinetics concepts, including laws, derivations, and scientific principles. These notes, available at no cost on Vedantu, offer an efficient study aid. Utilize this valuable resource to stay ahead in exam preparation and confidently navigate the competition. Accessing this FREE PDF ensures a thorough review, enabling a deeper understanding of the subject. Take advantage of Vedantu's commitment to accessible education and boost your academic performance by incorporating these revision notes into your study routine. Download now and reinforce your knowledge base for a more successful examination outcome.
Important Related Links for JEE Main and JEE Advanced
FAQs on Revision Notes on Chemical Kinetics for JEE Advanced 2026
1. What is collision theory?
In chemical kinetics, the reactant molecules collide with each other in a chemical reaction system and form new products. This is called collision theory.
2. What is collision frequency?
The number of collisions occurring in a chemical reaction per unit volume per second is called collision frequency. It is denoted by Z.
3. What are the barriers to reaction collisions?
As per the Chemical Kinetics notes for JEE Advanced, orientation and energy barriers are the two main barriers that collisions need to overcome to become effective.
4. What is radioactivity?
The emission of radioactive particles from the nucleus of a radioactive atom is called radioactivity. It follows the rules of 1st order chemical kinetics. It results in the formation of new elements from a radioactive heavy element.





























