



Introduction
Differential calculus is concerned with the rate at which one quantity changes in relation to another. You can also think of it as a study of quantity change rates. For instance, velocity is the rate at which a distance changes with respect to time in a specific direction. If f(x) is a function, the differential equation is f'(x) = dy/dx, where f'(x) is the function's derivative, y is the dependent variable, and x is the independent variable.
Important Terms in Differential Calculus
Function
Variable
Domain and Range
Limits
Continuity
Differentiability
Differentiation formulae
Tangent and Normal
Approximation
Rate measure
Maxima and Minima
Differential Equation
Limit
In calculus, the limit is extremely significant. In calculus, limits are used to define continuity, integrals, and derivatives. A function's limit is defined as follows:
Let's say the function "f" is defined on an open interval containing some numbers, such as "a," with the exception of "a" itself. The limit of a function f(x) is written as: \[\begin{array}{l}\lim_{x\rightarrow a}f(x)= L\end{array} \] ,iff given e > 0, there exists d > 0 such that 0 < |x – a| < d implies that |f(x) – L| < e It means that the limit f(x) as “x” approaches “a” is “L”.
Continuity
Continuity of a function states the characteristics of the function and its functional value. A function is said to be continuous if the curve has no missing points or breaking points in a given interval or domain, that is the curve is continuous at every point in its domain.
A function f(x) is known as a continuous function at a point x = a, in its domain if the following listed three conditions are satisfied-
f (a) exists which means that the value of f (a) is finite.
$\displaystyle \lim_{x \to a} f(x)$ exists, that is the right-hand limit = left-hand limit, and both R.H.S and L.H.S are finite.
$\displaystyle \lim_{x \to a} f(x)$ = f (a)
A function f(x) is said to be continuous in the given interval I that is equal to [x1, x2] only if the three conditions listed above are satisfied for every point in the given interval I.
Formal Definition of Continuity
A function is said to be continuous in the closed interval (a,b) if:
1. f is continuous in (a, b)
2. $\displaystyle \lim_{x \to a^{+}} f(x) = f(a)$
3. $\displaystyle \lim_{x \to a^{1}} f(x)= f(a)$
A function is said to be continuous in the open interval (a, b) if, f (x) is going to be continuous within the unbounded interval (a, b) if at any point within the given interval the function is continuous.
Differentiability
Function f(x) is said to be differentiable at the point x = a and if the derivative of the function f ‘(a) exists at every point in its given domain.
Differentiability Formula
The differentiability formula is defined by -
f’(a) = \[\frac{f(a+h)-f(a)}{h}\]
If a function is continuous at a particular point then a function is said to be differentiable at any point x = a in its domain. The vice versa of this is not always true.
Differentiation Formulae
Tangent and Normal
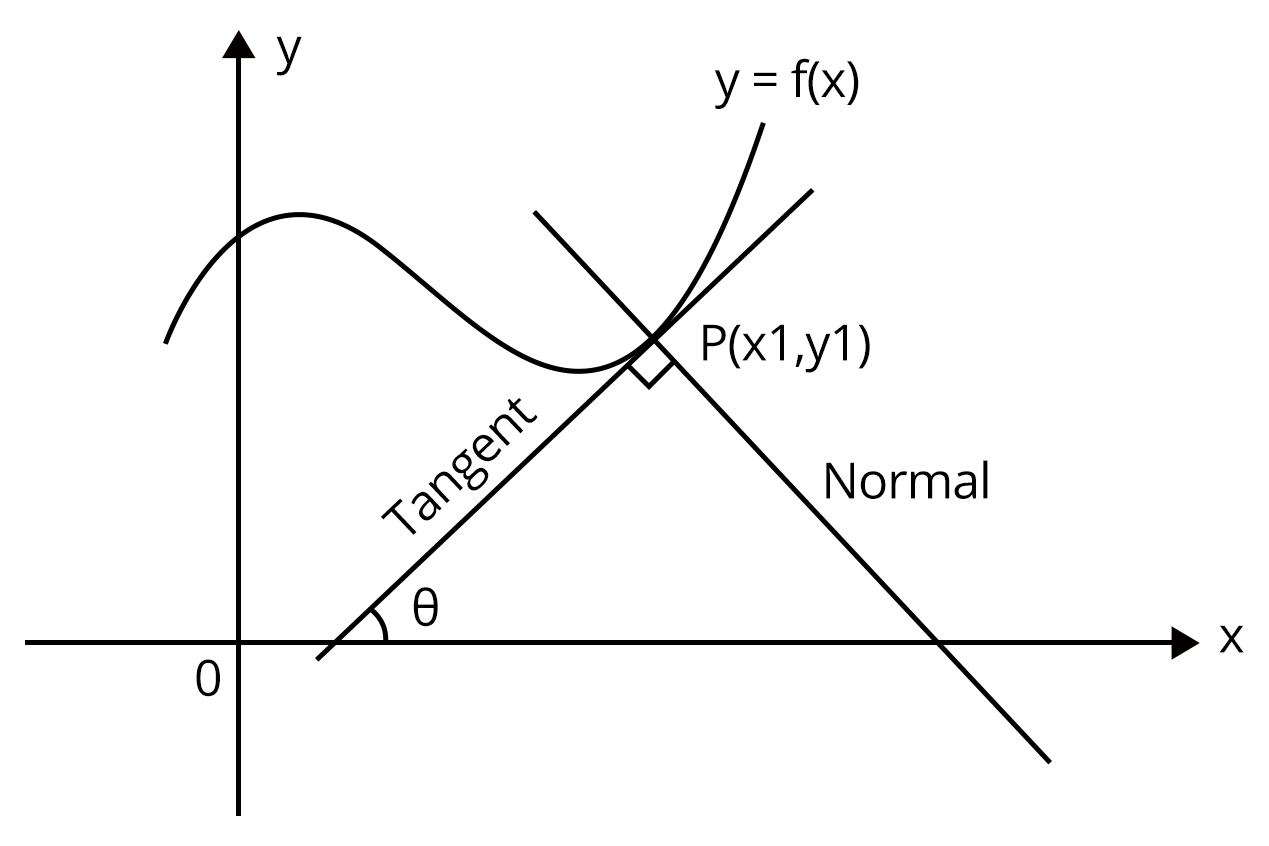
If tangent at P makes an angle $\theta$ with positive direction of x - axis, then slope of the tangent is $m = tan\theta$. Also, the slope of the tangent to the curve at any point on it is $\frac{dy}{dx}$.
$\therefore m = tan\theta =\frac{dy}{dx}$.
Also,the slope of normal is $-\frac{dx}{dy}$.
Therefore, equation of tangent at point $P\left ( x_{1}, \,\ y_{1} \right )$
$\Rightarrow \left ( y-y_{1} \right )= \frac{dy}{dx}_{\left ( x_{1}, \,\ y_{1} \right )}\left ( x_{1}, \,\ y_{1} \right )$.
And the equation of the normal at point $P\left ( x_{1}, \,\ y_{1} \right )$
$\Rightarrow \left ( y-y_{1} \right )= -\frac{dx}{dy}_{\left ( x_{1}, \,\ y_{1} \right )}\left ( x_{1}, \,\ y_{1} \right )$.
Approximation Using Derivative
Consider the following figure to recall the definition of derivatives of function $y = f(x)$ at some point $P\left ( x, \,\ f(x) \right )\,\ w.r.to..x$.
From the definition of derivatives, we have
$\frac{dy}{dx}=\displaystyle \lim_{x \to 0}\frac{\Delta y}{\Delta x}= \displaystyle \lim_{x \to 0}\frac{f\left ( x+\Delta x \right )-f(x)}{\Delta x}$.
Here, when point Q moves closer to point P on the curve, then though $\Delta x$ does not tend to zero, $\Delta y$.
In that case,
$\Rightarrow \frac{dy}{dx}=\frac{\Delta y}{\Delta x}= \frac{f\left ( x+\Delta x \right )-f(x)}{\Delta x}$.
$\therefore f\left ( x+\Delta x \right )=f(x)+\Delta x \,\ \frac{dy}{dx}$.
Monotonicity
One of the most important tools in analyzing the functions is their monotonic behavior. Functions like $f(x)= 2x+3, \,\ g(x)= log_{e}x \,\ and \,\ h(x) = x^{3}$ increase with the increase in the input value of the independent variable in their entire domain, i,e., graph of the function rises from left to right. Functions like $f(x)= cos^{-1}x$ and $g(x)= 0.5^{x}$ always decrease with increase in the value of x. Both of the above categories of functions are called monotonic functions.
Classification of functions based on monotonicity
Increasing Function
Strictly Increasing Function
Decreasing Function
Strictly Decreasing Function
Maxima and Minima
Consider the graph of one differential functions as shown in the following figure
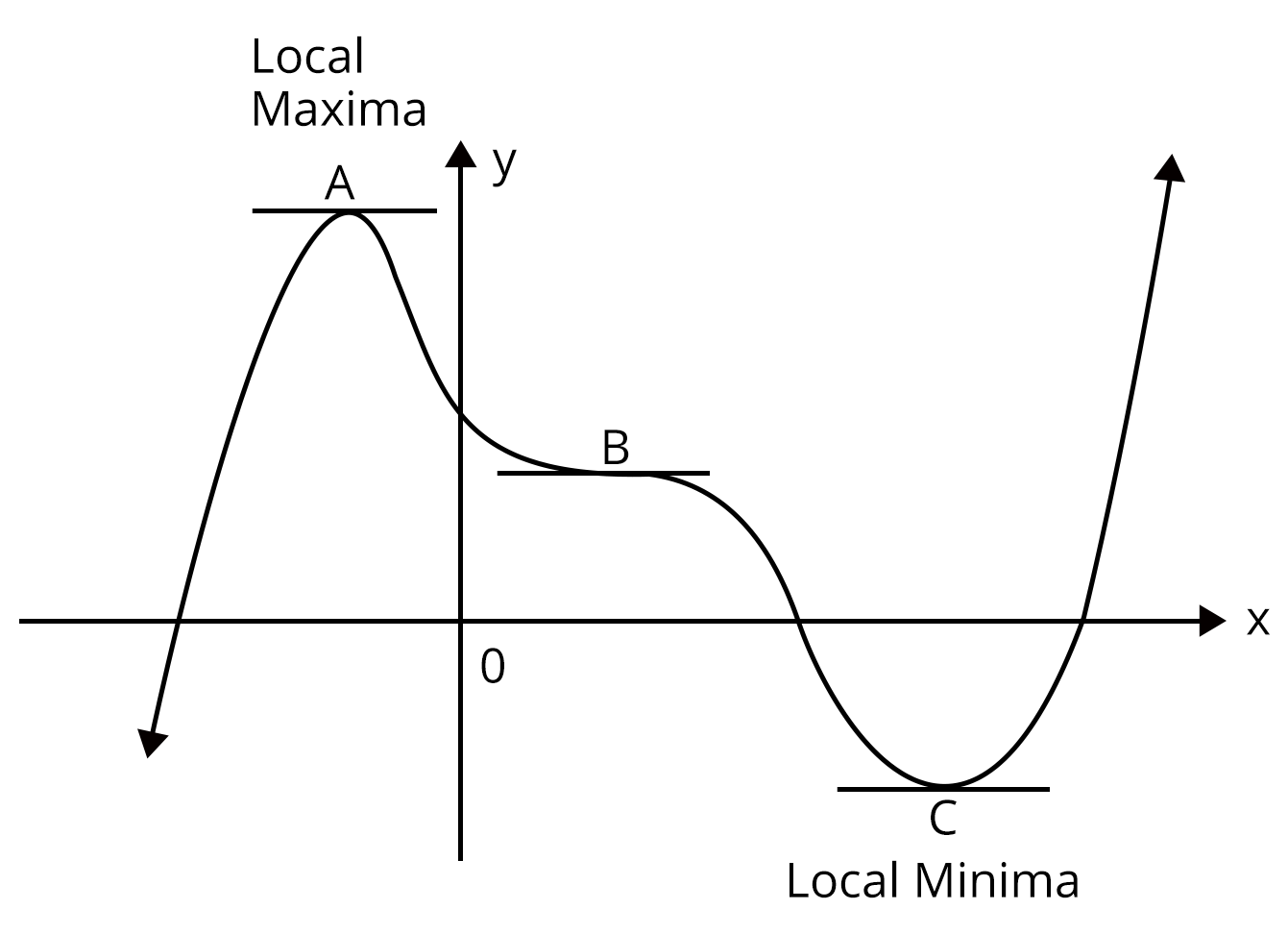
We observe that points A, B and C are stationary points where tangent to the curve is parallel to the x axis i.e., the derivative is zero. These two stationary points are referred to as turning points.
Point A in figure is called a point of local maxima because in its immediate area it is the highest point, and so represents the greatest or maximum value of the function in that area.
Point B is called a local minimum because in its immediate area it is the lowest point, and so represents the least or minimum value of the function in that area.
Solved Examples:
Example 1: If the equation of tangent to the curve $y^{2}=ax^{3}+b$ at point (2, 3) is y = 4x - 5, then find the values of a and b
Solution:
Here, we have $y^{2}=ax^{3}+b$ ……………(1)
Differentiating w.r.t, x , we get
$\Rightarrow 2y\frac{dy}{dx}= 3ax^{2}$
$\Rightarrow \frac{dy}{dx}=\frac{3ax^{2}}{2y}$
$\left ( \frac{dy}{dx} \right )_{\left ( 2,3 \right )}=\frac{3\times a\times \left ( 2 \right )^{2}}{2\times 3}=2a$
Now, line y = 4x - 5 is tangent to the curve at (2, 3).
$\therefore 2a = 4$
$\Rightarrow a = 2$
Also, (2, 3) lies on the curve(1)
$\Rightarrow 9 = 8a+b$
$\therefore b=-7$
Example 2: If the graph of the function $f(x) = 3x^{4}+2x^{3}+ax^{2}-x+2$ is concave upward for all real x, then find the values of a.
Solution:
Here, we have $f'(x) = 12x^{3}+6x^{2}+2ax-1$
And $f''(x) = 36x^{2}+12x+2a$
Now graph of concave upward for all real x.
$\therefore f''(x)=36x^{2}+12x+2a>0$ for all real x.
Then, discriminant, $12^{2}-4(36)(2a)<0$
$\Rightarrow 1-2a<0$
$\Rightarrow a >\frac{1}{2}$
Solved Problems of Previous Year Question
1. Let f, $f,g:\left [ -1,2 \right ]\to R$ be continuous functions which are twice differentiable on the interval (-1, 2). Let the values of f and g at the points -1, 0 and 2 be as given in the following table:
In each of the intervals (-1, 0) and (0, 2), the function (f-3g)’’ never vanishes. Then the correct statements is are
$f'(x)-3g'(x)=0$ has exactly three solutions in $\left ( -1,0 \right )\cup \left ( 0,2 \right )$.
$f'(x)-3g'(x)=0$ has exactly one solution in (-1, 0)
$f'(x)-3g'(x)=0$ has exactly one solution in (0, 2)
$f'(x)-3g'(x)=0$ has exactly two solutions in (-1, 0) and exactly two solutions in (0, 2)
Ans: (b), (c)
Let $h(x)=f(x)-3g(x)$
$h(-1)= f(-1)-3g(-1)=3-0=3$
$h(0)= f(0)-3g(0)=6-3=3$
$h(2)= f(2)-3g(2)=0-(-3)=3$
Thus, $h'(x)= 0$ has at least one root in (-1 , 1) and at least one root in (0, 2).
But Since $h''(x)= 0$ has no root in (-1, 0) and (0, 2) therefore $h'(x)= 0$ has exactly 1 root in (-1, 0) and exactly 1 root in (0, 2).
2. The function $f(x)=2\left|x \right|+\left|x +2 \right|+\left|\left|x+2 \right|-2\left|x \right| \right|$ has a local minimum or a local maximum at x =
$-2$
$\frac{-2}{3}$
$2$
$\frac{2}{3}$
Answer: a, b
$\Rightarrow \frac{f(x)=2\left|x \right|+\left|x +2 \right|+\left|\left|x+2 \right|-2\left|x \right| \right|}{2}=Min \, \left ( \left| 2x\right|, \left|x+2 \right| \right )$.
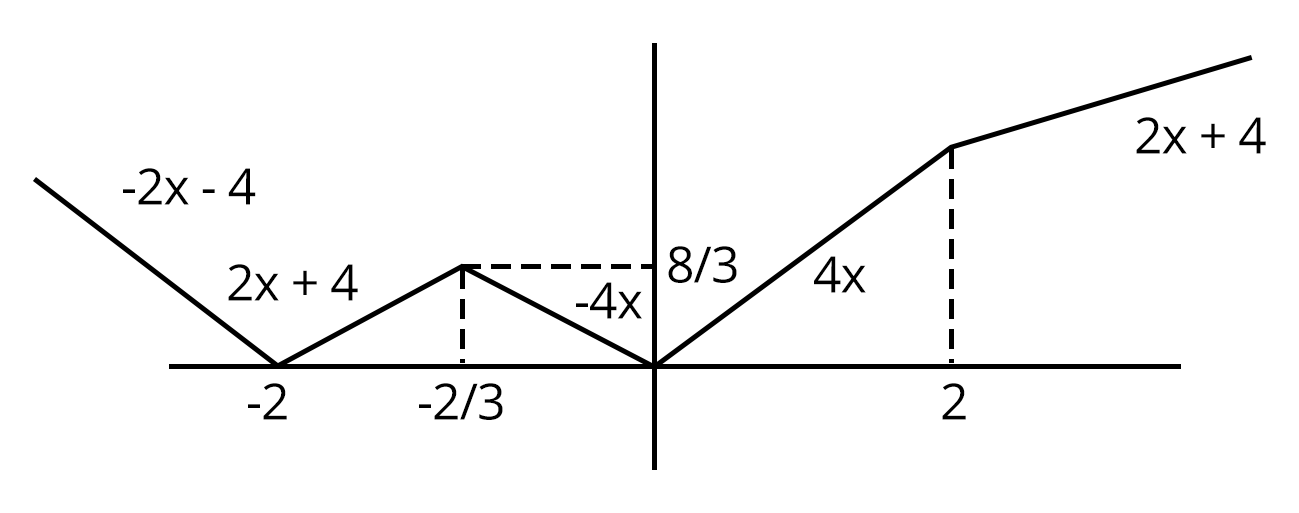
From the figure shown, points of local minima/ maxima are x = - 2, -⅔. 0
3. Let $a\in R$ and let $f:R\to R$ be given by $f(x)=x^{5}-5x+a$, then
f(x) has three real roots if a > 4
f(x) has only one real root if a > 4
f(x) has three real roots if a < - 4
f(x) has three roots if - 4 < a < 4
Ans: b, d
Let $y= f(x)=x^{5}-5x$
$\Rightarrow f'(x)= 5x^{4}-5$
$= 5(x-1)(x+1)(x^{2}+1)$
$f'(x)=0, \, \therefore x=-1,1$
$f''(x)= 20x^{3}$
$f''(1)= 20$ and $f''(-1)= -20$
Graph of y = f(x) is as shown in the following figure
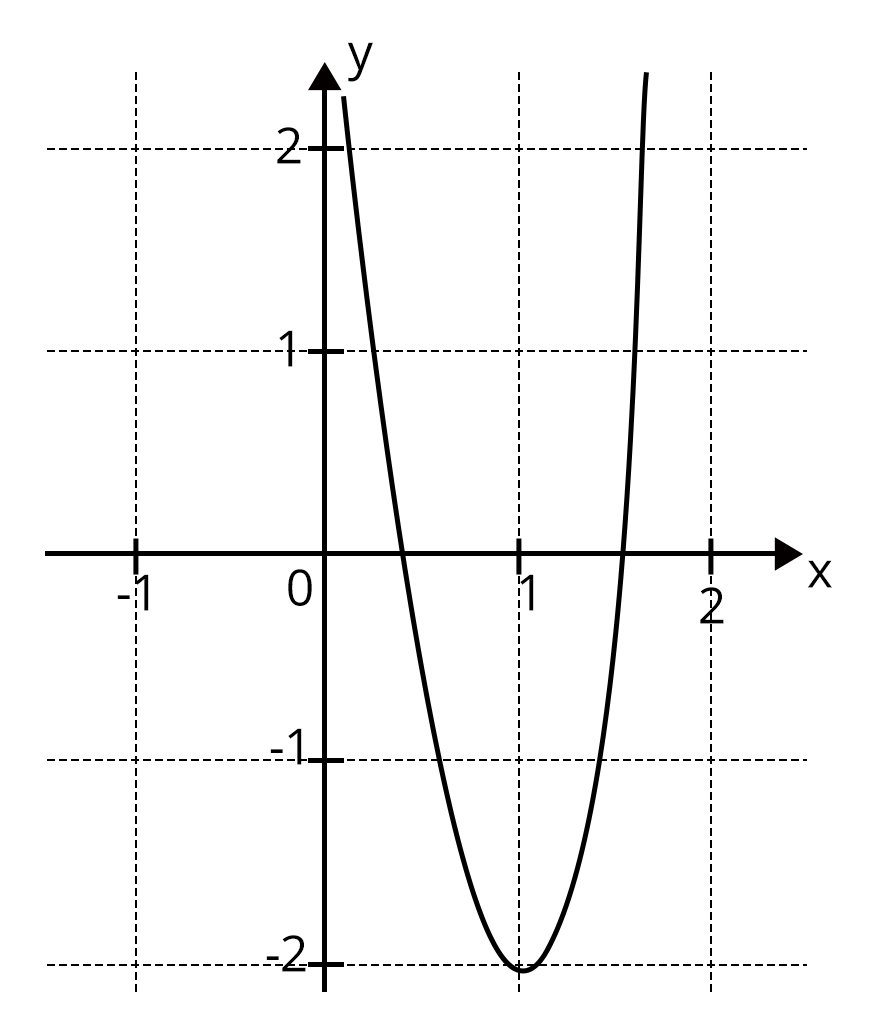
From the graph $x^{5}-5x=-a$ has one real root if $-a<-4$ or $-a>4$
$\Rightarrow a>4 \,\ or \,\ a<-4$
$x^{5}-5x = -a$ has three real roots if -4 < -a < 4 i.e., -4 < a < 4
Practice Question:
1. If f : R is a differentiable function such that $f'(x)> 2f(x)$ for all $x\in R$, and f(0) = 1, then
$f(x)>e^{2x}$ in $\left ( 0, \infty \right )$
f(x) is decreasing in $\left ( 0, \infty \right )$
f(x) is increasing in $\left ( 0, \infty \right )$
$f'(x)<e^{2x}$ in $\left ( 0, \infty \right )$
Answer: (a), (c)
2. The function $f : \left [ 0, 3 \right ]\to \left [ 1, 29 \right ]$ defined by $f(x)= 2x^{3}-15x^{2}+36x+1$, is
One - one and onto
Onto but not one one
One - one but not onto
Neither one - one nor onto
Answer: (b)
Conclusion:
In this chapter, we have elaborated on concepts and solutions to questions on the topic of Differential Calculus. Everything you're looking for is available in a single location. Students can carefully read through the Concepts, Definitions, and questions in the PDFs, which are also free to download and understand the concepts used to solve these questions. This will be extremely beneficial to the students in their exams.












FAQs on JEE - Differential Calculus
1. What are some applications of Derivatives in real-life examples?
Almost all the applications have some real-life usage when it comes to partial derivatives and absolute derivatives. When a value y varies with x such that it satisfies y=f(x), then f’(x) = dy/dx is called the rate of change of y with respect to x. Also, f’(x0) = dy/dx x=x0 is the rate of change of y with respect to x=x0. The rate of change of values is a significant application of differentiation, which is used broadly in physics and other engineering subjects.
2. What is the definition of tangent in Mathematics?
The tangent is a straight line that just touches the curve at a given point. The normal is a straight line that is perpendicular to the tangent. The tangent to any curve at a given point is observed to have the same gradient as the curve at that point. A derivative is required in order to find the gradient of the curve, which can be found by differentiating and obtaining an expression for dy/dx. The gradient of the tangent can be achieved by substituting an x-value. To find the full equation of the tangent, it remains to find the y-intercept of the tangent, which can be found using the coordinates of the point that the tangent and the curve have in the common.



