



Introduction to Analytic Geometry
Analytic Geometry is a branch of algebra that deals with the modelling of geometrical objects such as lines, points, curves, and so on. It is a major invention of Descartes and Fermat. It is a mathematical subject in which problems are solved using algebraic symbolism and methods. It establishes the mathematical equations' relationship with geometric curves. "Coordinate Geometry" is a word that is sometimes used to refer to analytic geometry.
Important Terms in Algebra
Planes
Cartesian Plane
Distance formula
Section Formula
Direction ratios
Locus
What is Analytical Geometry
Analytic geometry is a branch of Mathematics in which the position of a point on a plane can be determined using an ordered pair of numbers known as coordinates. This is also known as Cartesian geometry or coordinate geometry. Analytic geometry differs from synthetic geometry in that it does not use coordinates or formulae. To solve difficulties, it is regarded as an axiom or assumption. However, in analytic geometry, the geometrical objects are defined using local coordinates. This geometry is also defined using algebra.
Both two-dimensional and three-dimensional geometry use coordinate geometry. It's a symbol for geometrical shapes. Let's look at some of the terms used in analytic geometry, such as:
Plane
Coordinates
Coordinates
The two ordered pairs that specify the location of each given point in a plane are known as coordinates.
There are different types of coordinates in analytical geometry. Some of them are as follows:
Cartesian Coordinates
Polar Coordinates
Cylindrical Coordinates
Spherical Coordinates
Cartesian Coordinates
The Cartesian coordinate system is the most well-known coordinate system, in which each point has an x-coordinate and a y-coordinate that expresses its horizontal and vertical positions, respectively. They're frequently addressed as a pair and referred to as (x, y). This method can also be used in three-dimensional geometry, where each point in Euclidean space is represented by an ordered triple of coordinates (x, y, z).
Polar Coordinates
Each point in a plane is denoted by the distance 'r' from the origin and the angle θ from the polar axis in polar coordinates.
Cylindrical Coordinates
All points are represented in cylindrical coordinates by their height, radius from the z-axis, and angle projected on the xy-plane with regard to the horizontal axis. The letters h, r, and θ stand for height, radius, and angle, respectively.
Spherical Coordinates
The distance from the origin (ρ), the angle projected on the xy-plane with regard to the horizontal axis (θ), and another angle with respect to the z-axis (φ) are all used to describe a point in space in spherical coordinates.
Analytic Geometry Formulae in Two dimension
Distance Formula: Let the two points be A and B, having coordinates to be $\left ( x_{1}, \,\ y_{1} \right )$ and $\left ( x_{2}, \,\ y_{2} \right )$, respectively. Thus, the distance between two points is given as:
$\Rightarrow d = \sqrt{\left ( y_{2}-y_{1} \right )^{2}+\left ( x_{2}- x_{1} \right )^{2}}$
Section Formula: Let two lines A and B have coordinates $\left ( x_{1}, \,\ y_{1} \right )$, and $\left ( x_{2}, \,\ y_{2} \right )$, respectively. If the point P divides the two lines in the ratio of m:n, then the coordinates of P is given by,
When the ration m : n is internal,
$P\left ( x, \, y \right )= \left ( \frac{mx_{2}+nx_{1}}{m+n}, \, \frac{my_{2}+ny_{1}}{m+n} \right )$
When the ratio m : n is external,
$P\left ( x, \, y \right )= \left ( \frac{mx_{2}-nx_{1}}{m-n}, \, \frac{my_{2}-ny_{1}}{m-n} \right )$
Midpoint Formula: Let A and B are some points in a plane, which is joined to form a line, having coordinates $\left ( x_{1}, \,\ y_{1} \right )$ and $\left ( x_{2}, \,\ y_{2} \right )$, respectively. Suppose P(x, y) is the midpoint of the line connecting the point A and B, then its formula is given by,
$P\left ( x, y \right )= \left ( \frac{x_{1}+x_{2}}{2} , \frac{y_{1}+y_{2}}{2} \right )$
Angle Formula: Let two lines have slope $m_{1}$ and $m_{2}$ and θ is the angle formed between the two lines A and B, which is represented as:
$tan\theta = \left|\frac{m_{1}-m_{2}}{1+ m_{1}m_{2}} \right|$
Analytic Geometry in Three Dimensions
We examine real-number triples (a, b, c) and refer to this set as a three-dimensional number space, denoted by R'. Coordinates refer to all of the elements in a triple.
Let's look at how a geometric space represents a three-dimensional number space.
Consider three mutually perpendicular lines intersecting at point O in three-dimensional space. Starting at 0, these lines are designated as coordinate axes, with identical number scales set up on each of them.
Solved Examples
Example 1: The maximum value of $y = \sqrt{\left ( x-3 \right )^{2}+\left ( x^{2}-2 \right )^{2}}-\sqrt{x^{2}+\left ( x^{2}-1 \right )^{2}}$.
3
$\sqrt{10}$
$2\sqrt{5}$
None of these
Solution:(b) let y = f(x) = $\sqrt{\left ( x-3 \right )^{2}+\left ( x^{2}-2 \right )^{2}}-\sqrt{x^{2}+\left ( x^{2}-1 \right )^{2}}$
Note that the first radical sign describes the distance between $P(x, x^{2})$ and A(3, 2) whereas the second radical sign describes the distance between $P(x, x^{2})$ and B(0, 1).
Now $PA - PB \leq AB$ for possible positions of P.
Hence, $f(x)_{max} =$ distance between AB $= \sqrt{9+1}=\sqrt{10}$
Hence, option b is the correct answer.
Example 2: Number of values of $\alpha$ such that the points $\left ( \alpha , 6 \right )$, ( -5, 0), and (5, 0) form an isosceles triangle is
4
5
6
7
Solution: (b)
Here, we have $A\left ( \alpha ,6 \right )$, B(-5, 0), and C(5, 0).
If AB = AC, we get $\alpha = 0$.
Hence, we get one value of c,
If AC = BC, we get $\alpha = -3, 13$
$\alpha$ can take 5 values 0, 3, -3, 13, -13.
Hence, option (b) is the correct answer.
Solved Problems of Previous Year Question
1. The incentre of the triangle with vertices $(1, \sqrt{3})$, (0, 0), and (2, 0) is
$\left ( 1, \frac{\sqrt{3}}{2} \right )$
$\left ( \frac{2}{3}, \frac{1}{\sqrt{3}} \right )$
$\left ( \frac{2}{3}, \frac{\sqrt{3}}{2} \right )$
$\left ( 1, \frac{1}{\sqrt{3}} \right )$
Ans: (d) here, slides are equal.
So, it is an equilateral triangle.
Thus, the incentre is centroid.
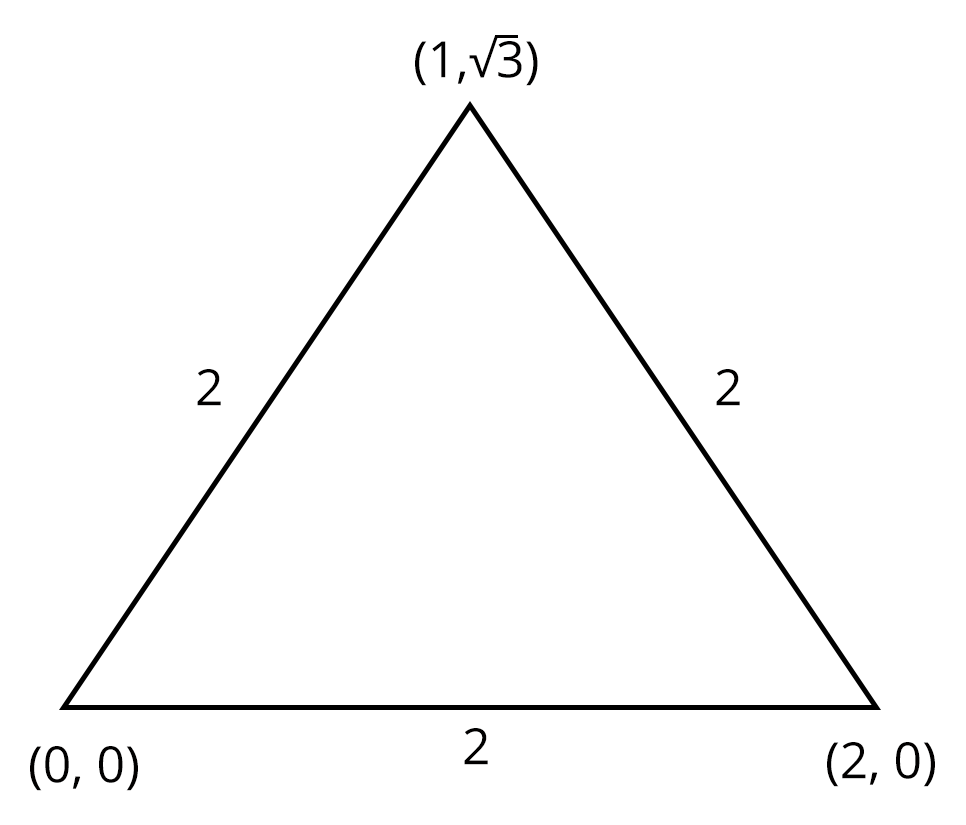
Incentre = $\left ( \frac{0+2+1}{3}, \frac{0+0+\sqrt{3}}{3} \right )$
$\Rightarrow \left ( 1, \frac{1}{\sqrt{3}} \right )$
Hence, option (d) is the correct answer.
2. Let PS be the median of the triangle with vertices P(2, 2), Q(6,-1), and R(7,3). The equation of the line passing through (1,-1) and parallel to PS is
2x - 9y -7 = 0
2x - 9y -11 = 0
2x + 9y -11 = 0
2x + 9y + 7 = 0
Answer: d
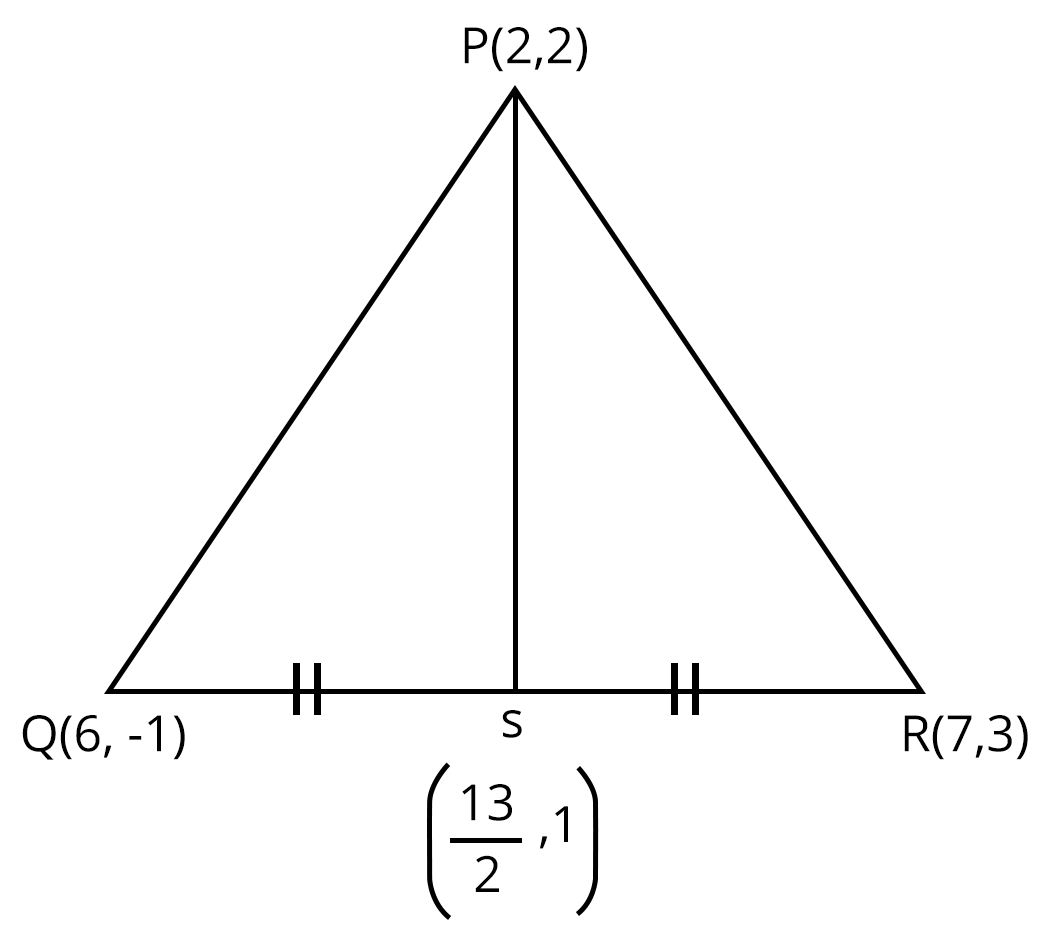
Here, midpoint of QR = (13/2, 1)
Now, slope of PS, $m_{ps}= \frac{2-1}{2-\frac{13}{2}}= \frac{1}{-\frac{9}{2}}= -\frac{2}{9}$
Passes through (1, -1)
$\Rightarrow y +1 = -\frac{2}{9}\left ( x - 1 \right )$
$\Rightarrow 2x + 9y + 7= 0$
3. A straight line through the origin O meets the parallel lines 4x + 2y = 9 and 2x + y + 6 = 0 at points P and Q, respectively. Then the point O divides the segment PQ in the ratio
1 : 2
3 : 4
2 : 1
4 : 3
Ans:
$L_{1} : 4x + 2y = 9$
$L_{2} : 2x + y + 6 = 0$
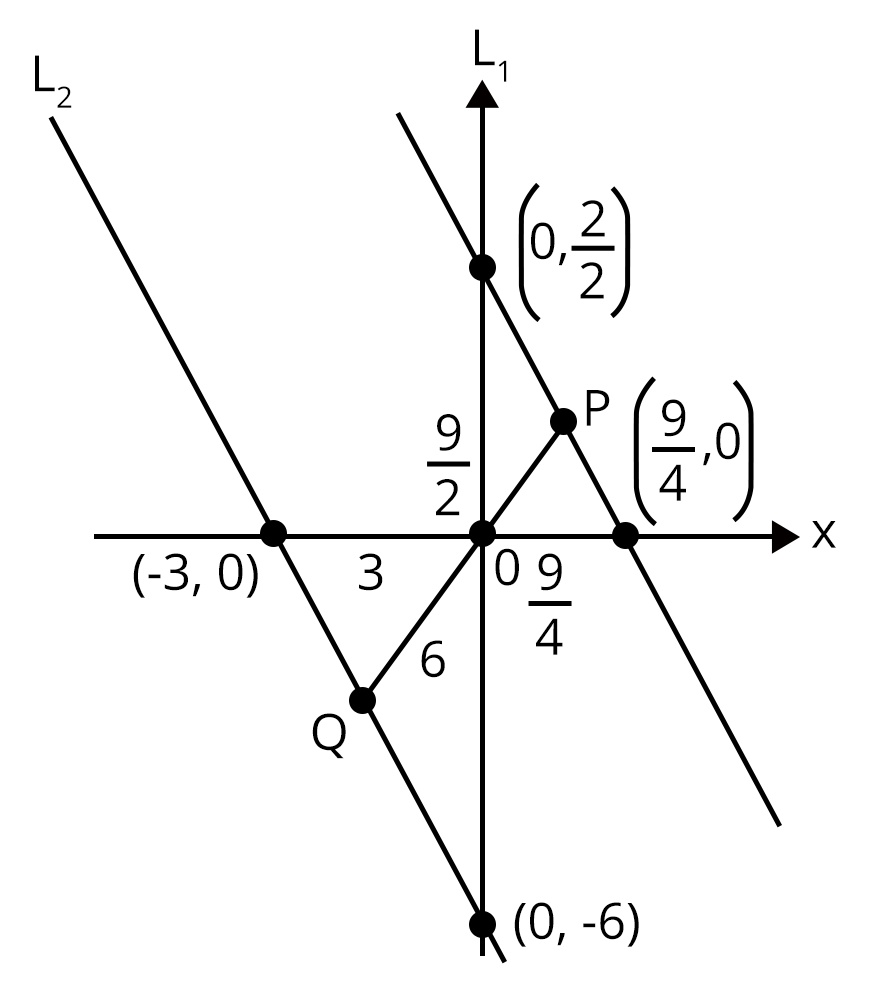
Perpendicular distance anyline passing through origin
$\Rightarrow \frac{9}{4}: 3 \Rightarrow 3 : 4$
$\Rightarrow \frac{9}{2}: 6 \Rightarrow 3 : 4$
$\Rightarrow \frac{9}{2\sqrt{5}} : \frac{6}{\sqrt{5}}\Rightarrow 3 : 4$
Practice Question
1. The number of triangles which are obtuse and which have the points (8, 9), (8, 16), and (20, 25) as the feet of perpendiculars drawn from the vertices on the opposite sides is
0
1
2
3
Answer: (d)
2. If A(5, 2), B(10, 12), and P(x, y) is such that AP/PB = 3/2, then the internal bisector of $\angle APB$ always passes through
(20, 32)
(8, 8)
(8,-8)
(-8, -8)
Answer: (b)
Conclusion
In this chapter, we have elaborated on concepts and solutions to questions on the topic of Analytic Geometry. Everything you're looking for is available in a single location. Students can carefully read through the concepts, definitions, and questions in the PDFs, which are also free to download, and understand the concepts used to solve these questions. This will be extremely beneficial to the students in their exams.












FAQs on JEE - Analytic Geometry
1. How do you find the intersecting point of the X-axis and Y-axis?
The initial point of intersection of the axis occurs at the origin where both the values of X and Y are represented as (x,y)= (0,0). Now if any two lines are drawn on the X/Y plane that are not parallel to each other, it is almost a certainty that the lines will intersect.
For instance, if you plot the x+2y=0 and x-2y=0 on a graph, these lines will intersect. But the question is at which point will they intersect each other. For finding the values of (x,y) at which both the lines intersect, you need to solve the equation of the lines, using a simultaneous linear equation.
2. What is the analytical geometry of three dimensions and its applications?
In three-dimensional space, we consider three mutually perpendicular lines intersecting in a point O and here we consider triples (a,b,c) which are real numbers and call this set a three-dimensional number space and denote it by R’.
Applications for analytic geometry are spread across a variety of fields and sciences. The application of analytical geometry in the engineering field and Physics is most mentionable among the others. It is also essentially related to other mathematical fields like trigonometry and analytic geometry and calculus and analytic geometry Chapter 3.
Get a complete grasp on the formulas for analytic geometry and also the application of the analytical geometry field through in-depth analysis, explanations, sums, and comprehensive assistance and tutorials from the experts.



