NCERT Exemplar for Class 9 Maths Chapter 2 - Polynomials (Book Solutions)

Multiple Choice questions

Sample Question 1: If \[{x^2}{\text{ }} + {\text{ }}kx{\text{ }} + {\text{ }}6{\text{ }} = {\text{ }}\left( {x{\text{ }} + {\text{ }}2} \right){\text{ }}\left( {x{\text{ }} + {\text{ }}3} \right)\] for all x, then the value of k is 

(A)  $ 1 $ 

(B)  $  - 1 $ 

(C)  $ 5 $ 

(D)  $ 3 $ 

Ans:  Option (C) is correct.

We have, \[{x^2}{\text{ }} + {\text{ }}kx{\text{ }} + {\text{ }}6{\text{ }} = {\text{ }}\left( {x{\text{ }} + {\text{ }}2} \right){\text{ }}\left( {x{\text{ }} + {\text{ }}3} \right)\]

Now, let’s taking RHS,

 $  \Rightarrow \left( {x + 2} \right)\left( {x + 3} \right) $ 

On multiplication, we get

 $  \Rightarrow {x^2} + 2x + 3x + 6 $ 

On addition, we get

 $  \Rightarrow {x^2} + 5x + 6 $ 

 Now on comparing LHS and RHS, we get

 $ k = 5 $ 

EXERCISE 2.1

Write the correct option in each of the following:

 1. Which of the following is a polynomial?

(A)  $ \dfrac{{{x^2}}}{2} - \dfrac{2}{{{x^2}}} $ 

(B) $ \sqrt {2x}  - 1 $ 

(C)  $ {x^2} + \dfrac{{3{x^{\dfrac{3}{2}}}}}{{\sqrt x }} $ 

(D)  $ \dfrac{{x - 1}}{{x + 1}} $ 

Ans: (C) is the correct option.

Polynomials are an algebraic expression that consist of variables and coefficients. Here the power of variables should be in whole number like 1,2,3 etc.

 (A)  $ \dfrac{{{x^2}}}{2} - \dfrac{2}{{{x^2}}} $ 

Here the coefficient  $  - 2 $  is multiplied with  $ {x^{ - 2}} $ . So here the power of x is not a whole number. Hence, it is not a Polynomial.

(B) $ \sqrt {2x}  - 1 $ 

Here the coefficient  $ \sqrt 2  $  is multiplied with  $ {x^{\dfrac{1}{2}}} $ . So here the power of x is not a whole number. Hence, it is not a Polynomial.

(C)  $ {x^2} + \dfrac{{3{x^{\dfrac{3}{2}}}}}{{\sqrt x }} $ 

Here the coefficient  $ 1 $  is multiplied with  $ {x^2} $  and the coefficient  $ 3 $  is multiplied with \[{x^{\dfrac{3}{2} - \dfrac{1}{2}}} = {x^{\dfrac{2}{2}}} = x\]  . So here the power of x is a whole number in the whole equation. Hence, it is a Polynomial.

(D)  $ \dfrac{{x - 1}}{{x + 1}} $ 

It is not a standard format of a Polynomial. Hence, it is not a Polynomial.

2. $ \sqrt 2  $ is a Polynomial of degree

(A)  $ 2 $ 

(B)  $ 0 $ 

(C)  $ 1 $ 

(D)  $ \dfrac{1}{2} $ 

Ans: Option (B) is correct.

Here  $ \sqrt 2  $  is a constant Polynomial. We can also write it as  $ \sqrt 2 {x^0} $ . Therefore, the degree of this Polynomial is  $ 0 $ .

3. Degree of the Polynomial of  $ 4{x^4} + 0{x^3} + 0{x^5} + 5x + 7 $ is

(A)  $ 4 $ 

(B)  $ 5 $ 

(C)  $ 3 $ 

(D)  $ 7 $ 

Ans: Option (A) is correct.

The highest power of x in the Polynomial is called the degree of Polynomial. We have the term with the highest power of x is  $ 4{x^4} $ , which is  $ 4 $ .

Therefore, the degree of Polynomial is  $ 4 $ .

4. Degree of the zero Polynomial

(A)  $ 0 $ 

(B)  $ 1 $ 

(C) Any natural number

(D) Not defined

Ans: Option (D) is the correct answer.

Like any constant value, the value 0 can be considered as a (constant) Polynomial, called the zero Polynomial. It has no nonzero terms, and so, strictly speaking, it has no degree either. Therefore, the degree of the zero Polynomial is not defined.

5. If  $ p\left( x \right) = {x^2} - 2\sqrt 2 x + 1 $ , then  $ p\left( {2\sqrt 2 } \right) $  is equal to

(A)  $ 0 $  

(B)  $ 1 $ 

(C)  $ 4\sqrt 2  $ 

(D)  $ 8\sqrt 2  + 1 $ 

Ans: The correct option is (B).

We have,

 $ p\left( x \right) = {x^2} - 2\sqrt 2 x + 1 $ 

Here, we have given the value of  $ x = 2\sqrt 2  $ .

 So, on putting the value in above equation, we get

 $ p\left( {2\sqrt 2 } \right) = {\left( {2\sqrt 2 } \right)^2} - 2\sqrt 2 \left( {2\sqrt 2 } \right) + 1 $ 

 $ p\left( {2\sqrt 2 } \right) = 4 \times 2 - 4 \times 2 + 1 $ 

 $ p\left( {2\sqrt 2 } \right) = 8 - 8 + 1 $ 

 $ p\left( {2\sqrt 2 } \right) = 1 $ 

6. The value of the Polynomial  $ 5x - 4{x^2} + 3 $ , when  $ x =  - 1 $  is

(A)  $  - 6 $ 

(B)  $ 6 $ 

(C)  $ 2 $ 

(D)  $  - 2 $ 

Ans: The correct option is (A).

Here we have given a Polynomial  $ 5x - 4{x^2} + 3 $ .

In this we have to put  $ x =  - 1 $ , and then we have to find the value of Polynomial

Therefore,

 $ p\left( x \right) = 5x - 4{x^2} + 3 $ 

 $ p\left( { - 1} \right) = 5\left( { - 1} \right) - 4{\left( { - 1} \right)^2} + 3 $ 

 $ p\left( { - 1} \right) =  - 5 - 4 + 3 $ 

 $ p\left( { - 1} \right) =  - 9 + 3 $ 

 $ p\left( { - 1} \right) =  - 6 $ 

7. If  $ p\left( x \right) = x + 3 $ , then  $ p\left( x \right) + p\left( { - x} \right) $  is equal to

(A)  $ 3 $ 

(B)  $ 2x $ 

(C)  $ 0 $ 

(D)  $ 6 $ 

Ans: The correct option is (D).

Here, we have  $ p\left( x \right) = x + 3 $ .

Now, on substituting  $ x $  with  $  - x $ , we get  $ p\left( { - x} \right) =  - x + 3 $ 

Now, on adding both the equations, we get

 $ p\left( x \right) + p\left( { - x} \right) = x + 3 - x + 3 $ 

 $ p\left( x \right) + p\left( { - x} \right) = 6 $ 

8. Zero of a zero Polynomial is 

(A)  $ 0 $ 

(B)  $ 1 $ 

(C) Any real number 

(D) Not defined

Ans: (C) is the correct answer.

Zero Polynomial is a constant Polynomial whose all coefficients are equal to 0. Zero of a Polynomial or we can say that root of a polynomial is the value of a variable that is responsible to make the Polynomial equals to zero. Hence, zero of the zero Polynomial is any real number.

9. Zero of the Polynomial  $ p\left( x \right) = 2x + 5 $  is

(A)  $  - \dfrac{2}{5} $ 

(B)  $  - \dfrac{5}{2} $ 

(C)  $ \dfrac{2}{5} $ 

(D)  $ \dfrac{5}{2} $ 

Ans: (B) is the correct option.

To get the zero of the Polynomial, we have to put the expression equals to zero.

 $ p\left( x \right) = 0 $ 

 $ 2x + 5 = 0 $ 

 $ 2x =  - 5 $ 

 $ x =  - \dfrac{5}{2} $ 

Therefore,  $  - \dfrac{5}{2} $  is the zero of the Polynomial.

10. One of the zeroes of given Polynomial  $ 2{x^2} + 7x - 4 $  is

(A)  $ 2 $ 

(B)  $ \dfrac{1}{2} $ 

(C)  $  - \dfrac{1}{2} $ 

(D)  $  - 2 $ 

Ans: (B) is the correct option.

To find the zeroes of a Polynomial, we have to put that expression equals to zero.

Therefore,

 $ 2{x^2} + 7x - 4 = 0 $ 

Using middle term splitting,

 $ 2{x^2} + \left( {8 - 1} \right)x - 4 = 0 $ 

 $ 2{x^2} + 8x - x - 4 = 0 $ 

 $ 2x\left( {x + 4} \right) - 1\left( {x + 4} \right) = 0 $ 

 $ \left( {2x - 1} \right)\left( {x + 4} \right) = 0 $ 

So, there we have two Ansutions

 $ 2x - 1 = 0 $  and  $ x + 4 = 0 $ 

 $ 2x = 1 $  and  $ x =  - 4 $ 

 $ x = \dfrac{1}{2} $  and  $ x =  - 4 $ 

11. If  $ {x^{51}} + 51 $  is divided by  $ x + 1 $ , the remainder is

(A)  $ 0 $ 

(B)  $ 1 $ 

(C)  $ 49 $ 

(D)  $ 50 $ 

Ans: Option (D) is the correct option.

Here we will use the remainder theorem.

If any Polynomial  $ f(x) $  is divided by  $ x - h $ , then the remainder will be  $ f\left( h \right) $ 

Here given Polynomial is  $ {x^{51}} + 51 $  and divided by  $ x + 1 $ 

So, by using the remainder theorem we can say that

Remainder=  $ f\left( { - 1} \right) $  since the divisor is  $ x + 1 $ 

Therefore we can write it as

\[ \Rightarrow f(x) = {x^{51}} + 51\]

\[ \Rightarrow f( - 1) = {( - 1)^{51}} + 51\]

\[ \Rightarrow f( - 1) =  - 1 + 51\]

\[\therefore f( - 1) = 50\]

12. If  $ x + 1 $ , is a factor of the Polynomial  $ 2{x^2} + kx $ , then the value of k is

(A)  $  - 3 $ 

(B)  $ 4 $ 

(C)  $ 2 $ 

(D)  $  - 2 $ 

Ans: Option (C) is correct.

Let  $ p\left( x \right) = 2{x^2} + kx $ 

Since, \[\left( {x{\text{ }} + {\text{ }}1} \right)\] is a factor of \[p\left( x \right)\], then

Using, factor theorem

\[ \Rightarrow p\left( { - 1} \right) = 0\]

\[ \Rightarrow 2{\left( { - 1} \right)^2} + {\text{ }}k\left( { - 1} \right){\text{ }} = {\text{ }}0\]

\[ \Rightarrow \;2 - k{\text{ }} = {\text{ }}0\]

\[ \Rightarrow \;k = {\text{ }}2\]

Therefore, the value of k is  $ 2 $ .

13.  $ x + 1 $ , is a factor of the Polynomial

(A)  $ {x^3} + {x^2} - x + 1 $ 

(B)  $ {x^3} + {x^2} + x + 1 $ 

(C)  $ {x^4} + {x^3} + {x^2} + 1 $ 

(D)  $ {x^4} + 3{x^3} + 3{x^2} + x + 1 $ 

Ans: (B) is the correct option.

 If  $ x + 1 $  is the factor of the Polynomial, then  $ x =  - 1 $  is the root of the Polynomial.

(A) Let  $ p\left( x \right) = {x^3} + {x^2} - x + 1 $ 

Now, put  $ x =  - 1 $ .

 $ p\left( { - 1} \right) = {\left( { - 1} \right)^3} + {\left( { - 1} \right)^2} - \left( { - 1} \right) + 1 $ 

 $ p\left( { - 1} \right) =  - 1 + 1 + 1 + 1 $ 

 $ p\left( { - 1} \right) = 2 $ 

Therefore,  $ p\left( { - 1} \right) \ne 0 $ .

So,  $ x + 1 $  is not a factor of the  $ p\left( x \right) $ .

(B) Let  $ p\left( x \right) = {x^3} + {x^2} + x + 1 $ 

Now, put  $ x =  - 1 $ .

 $ p\left( { - 1} \right) = {\left( { - 1} \right)^3} + {\left( { - 1} \right)^2} + \left( { - 1} \right) + 1 $ 

 $ p\left( { - 1} \right) =  - 1 + 1 - 1 + 1 $ 

 $ p\left( { - 1} \right) = 0 $ 

Therefore,  $ p\left( { - 1} \right) = 0 $ .

So,  $ x + 1 $  is a factor of the  $ p\left( x \right) $ .

(C) Let  $ p\left( x \right) = {x^4} + {x^3} + {x^2} + 1 $ 

Now, put  $ x =  - 1 $ .

 $ p\left( { - 1} \right) = {\left( { - 1} \right)^4} + {\left( { - 1} \right)^3} + {\left( { - 1} \right)^2} + 1 $ 

 $ p\left( { - 1} \right) = 1 - 1 + 1 + 1 $ 

 $ p\left( { - 1} \right) = 2 $ 

Therefore,  $ p\left( { - 1} \right) \ne 0 $ .

So,  $ x + 1 $  is not a factor of the  $ p\left( x \right) $ .

(D) Let  $ p\left( x \right) = {x^4} + 3{x^3} + 3{x^2} + x + 1 $ 

Now, put  $ x =  - 1 $ .

 $ p\left( { - 1} \right) = {\left( { - 1} \right)^4} + 3{\left( { - 1} \right)^3} + 3{\left( { - 1} \right)^2} + \left( { - 1} \right) + 1 $ 

 $ p\left( { - 1} \right) = 1 - 3 + 3 - 1 + 1 $ 

 $ p\left( { - 1} \right) = 1 $ 

Therefore,  $ p\left( { - 1} \right) \ne 0 $ .

So,  $ x + 1 $  is not the factor of the  $ p\left( x \right) $ .

14. One of the factor of  $ \left( {25{x^2} - 1} \right) + {\left( {1 + 5x} \right)^2} $  is

(A)  $ 5 + x $ 

(B)  $ 5 - x $ 

(C)  $ 5x - 1 $ 

(D)  $ 10x $ 

Ans: (D) is the correct option.

 $  \Rightarrow \left( {25{x^2} - 1} \right) + {\left( {1 + 5x} \right)^2} $ 

 $  \Rightarrow \left( {{{\left( {5x} \right)}^2} - {{\left( 1 \right)}^2}} \right) + {\left( {5x + 1} \right)^2} $ 

 $  \Rightarrow \left( {5x + 1} \right)\left( {5x - 1} \right) + {\left( {5x + 1} \right)^2} $ 

Now, taking common  $ \left( {5x + 1} \right) $ 

 $  \Rightarrow \left( {5x + 1} \right)\left( {\left( {5x - 1} \right) + \left( {5x + 1} \right)} \right) $ 

 $  \Rightarrow \left( {5x + 1} \right)\left( {5x - 1 + 5x + 1} \right) $ 

 $  \Rightarrow \left( {5x + 1} \right)\left( {10x} \right) $ 

Therefore, one of the factor of  $ \left( {25{x^2} - 1} \right) + {\left( {1 + 5x} \right)^2} $  is  $ 10x $ .

15. The value of  $ {249^2} - {248^2} $  is 

(A)  $ {1^2} $ 

(B)  $ 477 $ 

(C)  $ 487 $ 

(D)  $ 497 $ 

Ans: (D) is the correct option.

Here we will use the identity  $ {a^2} - {b^2} = \left( {a + b} \right)\left( {a - b} \right) $.

We have, 

  $  \Rightarrow {249^2} - {248^2} $ 

 $  \Rightarrow \left( {249 - 248} \right)\left( {249 + 248} \right) $ 

 $  \Rightarrow \left( 1 \right)\left( {497} \right) $ 

 $  \Rightarrow 497 $ 

16. The factorization of  $ 4{x^2} + 8x + 3 $  is

(A)  $ \left( {x + 1} \right)\left( {x + 3} \right) $ 

(B)  $ \left( {2x + 1} \right)\left( {2x + 3} \right) $ 

(C)  $ \left( {2x + 2} \right)\left( {2x + 5} \right) $ 

(D)  $ \left( {2x - 1} \right)\left( {2x - 3} \right) $ 

Ans: (B) is the correct option.

In this question, we will use middle term splitting for factorization

 $  \Rightarrow 4{x^2} + 8x + 3 $ 

We can also write it as,

 $  \Rightarrow 4{x^2} + 6x + 2x + 3 $ 

 $  \Rightarrow 2x\left( {2x + 3} \right) + 1\left( {2x + 3} \right) $ 

 $  \Rightarrow \left( {2x + 1} \right)\left( {2x + 3} \right) $ 

17. Which of the followings is factor of  $ {\left( {x + y} \right)^3} - \left( {{x^3} + {y^3}} \right) $ ?

(A)  $ {x^2} + {y^2} + 2xy $ 

(B)  $ {x^2} + {y^2} - xy $ 

(C)  $ x{y^2} $ 

(D)  $ 3xy $ 

Ans: (D) is the correct option.

We have,  $ {\left( {x + y} \right)^3} - \left( {{x^3} + {y^3}} \right) $ .

Now, in this question we will use the identity  $ {\left( {a + b} \right)^3} = {a^3} + {b^3} + 3ab\left( {a + b} \right) $ 

 $  \Rightarrow {x^3} + {y^3} + 3xy\left( {x + y} \right) - \left( {{x^3} + {y^3}} \right) $ 

 $  \Rightarrow 3xy\left( {x + y} \right) $ 

So, we can say that  $ 3xy $  is a factor of  $ {\left( {x + y} \right)^3} - \left( {{x^3} + {y^3}} \right) $ .

18. The coefficient of  variable x in the expansion  $ {\left( {x + 3} \right)^3} $ is 

(A)  $ 1 $ 

(B)  $ 9 $ 

(C)  $ 18 $ 

(D)  $ 27 $ 

Ans: (D) is the correct option.

Here in this question, we will use the identity  $ {\left( {a + b} \right)^3} = {a^3} + {b^3} + 3ab\left( {a + b} \right) $ 

Therefore, 

 $ {\left( {x + 3} \right)^3} = {x^3} + {3^3} + 3 \times x \times 3\left( {x + 3} \right) $ 

 $ {\left( {x + 3} \right)^3} = {x^3} + 27 + 9{x^2} + 27x $ 

Therefore, the coefficient of x is  $ 27 $ .

19. If  $ \dfrac{x}{y} + \dfrac{y}{x} =  - 1 $  the value of  $ {x^3} - {y^3} $  is

(A)  $ 1 $ 

(B)  $  - 1 $ 

(C)  $ 0 $ 

(D)  $ \dfrac{1}{2} $ 

Ans: The correct option is (C).

Here, it is given that   $ \dfrac{x}{y} + \dfrac{y}{x} =  - 1 $ 

On taking LCM, we get

 $ \dfrac{{{x^2} + {y^2}}}{{xy}} =  - 1 $ 

On cross-multiplication, we get

 $ {x^2} + {y^2} =  - xy $ 

Now, we know that

 $ {x^3} - {y^3} = \left( {x - y} \right)\left( {{x^2} + {y^2} + xy} \right) $ 

On putting  $ {x^2} + {y^2} =  - xy $  in above equation, we get

 $ {x^3} - {y^3} = \left( {x - y} \right)\left( { - xy + xy} \right) $ 

 $ {x^3} - {y^3} = \left( {x - y} \right)\left( 0 \right) $ 

 $ {x^3} - {y^3} = 0 $ 

20. If  $ 49{x^2} - b = \left( {7x + \dfrac{1}{2}} \right)\left( {7x - \dfrac{1}{2}} \right) $  , then the value of b is

(A)   $ 0 $ 

(B)  $ \dfrac{1}{{\sqrt 2 }} $ 

(C)  $ \dfrac{1}{4} $ 

(D)  $ \dfrac{1}{2} $ 

Ans: (C) is the correct option.

 Here in this question, we will use the identity  $ {a^2} - {b^2} = \left( {a + b} \right)\left( {a - b} \right) $ 

 $  \Rightarrow 49{x^2} - b = \left( {7x + \dfrac{1}{2}} \right)\left( {7x - \dfrac{1}{2}} \right) $ 

 $  \Rightarrow 49{x^2} - b = {\left( {7x} \right)^2} - {\left( {\dfrac{1}{2}} \right)^2} $ 

 $  \Rightarrow 49{x^2} - b = 49{x^2} - {\left( {\dfrac{1}{2}} \right)^2} $ 

On comparing, we get 

 $ b = {\left( {\dfrac{1}{2}} \right)^2} $ 

 $ b = \dfrac{1}{4} $ 

21. If  $ a + b + c = 0 $ ,  then the value of  $ {a^3} + {b^3} + {c^3} $  is equal to

(A)  $ 0 $ 

(B)  $ abc $ 

(C)  $ 3abc $ 

(D)  $ 2abc $ 

Ans: (C) is the correct option.

Here we know an identity, 

 $ {a^3} + {b^3} + {c^3} - 3abc = \left( {a + b + c} \right)\left( {{a^2} + {b^2} + {c^2} - ab - bc - ca} \right) $ 

It is given that, $ a + b + c = 0 $ 

Therefore, put it in the above equation

 $  \Rightarrow {a^3} + {b^3} + {c^3} - 3abc = \left( 0 \right)\left( {{a^2} + {b^2} + {c^2} - ab - bc - ca} \right) $ 

 $  \Rightarrow {a^3} + {b^3} + {c^3} - 3abc = 0 $ 

 $  \Rightarrow {a^3} + {b^3} + {c^3} = 3abc $ 

Short Answer Questions with Reasoning

Sample Question 1: Write whether the following statements are True or False.

Justify your answer.

(i)  $ \dfrac{1}{{\sqrt 5 }}{x^{\dfrac{1}{2}}} + 1 $  is a polynomial

Ans: It is a false statement.

Here, the exponent of a variable is not a whole number. So, it is not a polynomial.

(ii)  $ \dfrac{{6\sqrt x  + {x^{\dfrac{3}{2}}}}}{{\sqrt x }} $  is a polynomial,  $ x \ne 0 $ 

Ans: It is a true statement.

We can also write it as, 

 $ \dfrac{{6\sqrt x  + {x^{\dfrac{3}{2}}}}}{{\sqrt x }} = \dfrac{{\sqrt x {{\left( {6 + x} \right)}^{}}}}{{\sqrt x }} = 6 + x $ 

Here, the exponent of variable is not a whole number. So, it is a polynomial.

EXERCISE 2.2

1. Which of the following expressions are Polynomials? Justify your answer.

(i)  $ 8 $ 

Ans:  Here we have given an expression  $ 8 $ in which the degree of variable is zero. Therefore, it is a constant Polynomial.

(ii)  $ \sqrt 3 {x^2} - 2x $ 

Ans: $ \sqrt 3 {x^2} - 2x $ 

Here, in each term the power of x is a whole number. Therefore, this expression is a Polynomial.

(iii)  $ 1 - \sqrt {5x}  $ 

Ans: $ 1 - \sqrt {5x}  $ 

We can also write it as  $ 1 - \sqrt 5 {x^{\dfrac{1}{2}}} $ . Here the degree of variable is not a whole number. Therefore, this expression is not a Polynomial.

(iv)  $ \dfrac{1}{{5{x^{ - 2}}}} + 5x + 7 $ 

Ans: $ \dfrac{1}{{5{x^{ - 2}}}} + 5x + 7 $ 

We can also write it as  $ \dfrac{{1{x^2}}}{5} + 5x + 7 $ . Here in this expression each variable term has the power of x in a whole number. Therefore, this expression is a Polynomial.

(v)  $ \dfrac{{\left( {x - 2} \right)\left( {x - 4} \right)}}{x} $ 

Ans: $ \dfrac{{\left( {x - 2} \right)\left( {x - 4} \right)}}{x} $ 

We can also write it as 

 $ \dfrac{{{x^2} - 6x + 8}}{x} = x - 6 + \dfrac{8}{x} = x - 6 + 8{x^{ - 1}} $ 

Here, the exponent of variable x in the third term  $ 8{x^{ - 1}} $  is – 1, and this is not a whole number.

 Therefore, this algebraic expression is not a Polynomial.

(vi)  $ \dfrac{1}{{x + 1}} $

Ans: $ \dfrac{1}{{x + 1}} $ 

We can also reduce it to  $ {\left( {x + 1} \right)^{ - 1}} $ , which cannot be reduced to an expression in which the exponent of the variable x had only whole numbers in each of its terms. Therefore, this algebraic expression is not a Polynomial.

(vii)  $ \dfrac{1}{7}{a^3} - \dfrac{2}{{\sqrt 3 }}{a^2} + 4a - 7 $ 

Ans: $ \dfrac{1}{7}{a^3} - \dfrac{2}{{\sqrt 3 }}{a^2} + 4a - 7 $ 

In this expression, the exponent of a in each term is a whole number, so this expression is a Polynomial.

(viii)  $ \dfrac{1}{{2x}} $ 

Ans: $ \dfrac{1}{{2x}} $ 

We can also write it as  $ \dfrac{1}{2}{x^{ - 1}} $ . Here, the exponent of the variable x is   $  - 1 $  , which is not a whole number so, this algebraic expression is not a Polynomial.

2. Write whether the following statements are True or False. Justify your answer. 

(i) A binomial can have at most two terms 

Ans: The given statement is False because binomials have exactly two terms.

(ii) Every Polynomial is a binomial 

Ans: Every Polynomial cannot be a binomial because a Polynomial had many terms but a binomial had only two terms in the expression. For example,  $ {x^4} + {x^3} + {x^2} + x + 1 $ is a Polynomial but not a binomial. Therefore, the given statement is false.

(iii) A binomial may have degree  $ 5 $ 

Ans: The given statement is True because a binomial is a Polynomial whose degree is a whole number and it is greater than or equals to one and contain two terms. For example,  $ {x^5} - 1 $  is a binomial of degree  $ 5 $ .

(iv) Zero of a Polynomial is always  $ 0 $  

Ans: The given statement is False, because zero of Polynomial can be any real number.

(v) A Polynomial can't have more than one zeros 

Ans: The given statement is False, because a Polynomial can have any number of zeroes which depends on the degree of the Polynomial.

(vi) The power of the sum of two polynomials each of whose degree  $ 5 $  is always  $ 5 $ .

Ans: The given statement is False. For example, consider the two Polynomials  $  - {x^5} + 3{x^2} + 4 $  and  $ {x^5} + {x^4} + 2{x^3} + 3 $ .The degree of each of these polynomials will be 5. Their sum is  $ {x^4} + 2{x^3} + 3{x^2} + 7 $ . The degree of this Polynomial is  $ 4 $  not  $ 5 $ .

Short Answer Questions

Sample Question 1: (i) Check whether p(x) is a multiple of g(x) or not, where \[\;p\left( x \right) = {x^3}-{\text{ }}x + 1,\,{\text{ }}g\left( x \right) = 2-3x\]

Ans: p(x) will be a multiple of g(x) if and only if g(x) divides p(x). 

Now,  $ g\left( x \right) = 2 - 3x $ 

But,  $ g\left( x \right) = 0 $ 

 $  \Rightarrow 2 - 3x = 0 $ 

 $  \Rightarrow x = \dfrac{2}{3} $ 

Now, put  $ x = \dfrac{2}{3} $ in equation \[\;p\left( x \right) = {x^3}-{\text{ }}x + 1\]

\[\;p\left( {\dfrac{2}{3}} \right) = {\left( {\dfrac{2}{3}} \right)^3}-{\text{ }}\left( {\dfrac{2}{3}} \right) + 1\]

\[\;p\left( {\dfrac{2}{3}} \right) = \dfrac{8}{{27}} + \dfrac{1}{3} = \dfrac{{8 + 9}}{{27}} = \dfrac{{17}}{{27}}\]

Here, the remainder is not equals to zero.

Therefore, g(x) is not a multiple of p(x).

(ii) Check whether g(x) is a factor of p(x) or not, where \[p\left( x \right) = {\text{ }}8{x^3}-6{x^2}-4x + 3,{\text{ }}g\left( x \right) = {\text{ }}\dfrac{x}{3} - \dfrac{1}{4}\]

Ans: p(x) will be a multiple of g(x) if and only if g(x) divides p(x). 

Now,  $ g\left( x \right) = \dfrac{x}{3} - \dfrac{1}{4} $ 

But,  $ g\left( x \right) = 0 $ 

 $  \Rightarrow \dfrac{x}{3} - \dfrac{1}{4} = 0 $ 

 $  \Rightarrow x = \dfrac{3}{4} $ 

Now, put  $ x = \dfrac{3}{4} $ in equation \[p\left( x \right) = {\text{ }}8{x^3}-6{x^2}-4x + 3\]

\[p\left( {\dfrac{3}{4}} \right) = {\text{ }}8{\left( {\dfrac{3}{4}} \right)^3}-6{\left( {\dfrac{3}{4}} \right)^2}-4\left( {\dfrac{3}{4}} \right) + 3\]

\[p\left( {\dfrac{3}{4}} \right) = {\text{ }}8\left( {\dfrac{{27}}{{64}}} \right)-6\left( {\dfrac{9}{{16}}} \right)-3 + 3\]

\[p\left( {\dfrac{3}{4}} \right) = {\text{ }}\left( {\dfrac{{27}}{8}} \right)-\left( {\dfrac{{27}}{8}} \right)-3 + 3 = 0\]

Here, the remainder is equals to zero.

Therefore, g(x) is a multiple of p(x).

Sample Question 2: Find the value of a, if \[x-a\] is a factor of \[{x^3}-a{x^2}{\text{ }} + {\text{ }}2x{\text{ }} + {\text{ }}a{\text{ }}-{\text{ }}1\].

Ans: Here, \[p\left( x \right) = {x^3}-a{x^2}{\text{ }} + {\text{ }}2x{\text{ }} + {\text{ }}a{\text{ }}-{\text{ }}1\]

If \[x-a\] is a factor of p(x). Then,  $ p\left( a \right) = 0 $ 

\[ \Rightarrow {a^3}-a{\left( a \right)^2}{\text{ }} + {\text{ }}2\left( a \right){\text{ }} + {\text{ }}a{\text{ }}-{\text{ }}1 = 0\]

 $  \Rightarrow 3a - 1 = 0 $ 

 $  \Rightarrow a = \dfrac{1}{3} $ 

Therefore,  $ a = \dfrac{1}{3} $ .

Sample Question 3: (i) Without actually calculating the cubes, find the value of \[{48^3}{\text{ }}-{\text{ }}{30^3}{\text{ }}-{\text{ }}{18^3}\].

Ans: We know that, \[{x^3}{\text{ }} + {\text{ }}{y^3}{\text{ }} + {\text{ }}{z^3}{\text{ }}-{\text{ }}3xyz{\text{ }} = {\text{ }}\left( {x{\text{ }} + {\text{ }}y{\text{ }} + {\text{ }}z} \right){\text{ }}\left( {{x^2}{\text{ }} + {\text{ }}{y^2}{\text{ }} + {\text{ }}{z^2}{\text{ }}-{\text{ }}xy{\text{ }}-{\text{ }}yz{\text{ }}-{\text{ }}zx} \right)\]

If,  $ x + y + z = 0 $ 

Then, \[{x^3}{\text{ }} + {\text{ }}{y^3}{\text{ }} + {\text{ }}{z^3}{\text{  =  }}3xyz{\text{ }}\]

 Here,  $ 48 - 30 - 18 = 0 $ 

Therefore,  \[{48^3}{\text{ }}-{\text{ }}{30^3}{\text{ }}-{\text{ }}{18^3} = 3\left( {48} \right)\left( { - 30} \right)\left( { - 18} \right) = 77760\]

(ii)Without finding the cubes, factorise \[{\left( {x{\text{ }}-{\text{ }}y} \right)^3}{\text{ }} + {\text{ }}{\left( {y{\text{ }}-{\text{ }}z} \right)^3}{\text{ }} + {\text{ }}{\left( {z{\text{ }}-{\text{ }}x} \right)^3}\] .

Ans: We know that, \[{x^3}{\text{ }} + {\text{ }}{y^3}{\text{ }} + {\text{ }}{z^3}{\text{ }}-{\text{ }}3xyz{\text{ }} = {\text{ }}\left( {x{\text{ }} + {\text{ }}y{\text{ }} + {\text{ }}z} \right){\text{ }}\left( {{x^2}{\text{ }} + {\text{ }}{y^2}{\text{ }} + {\text{ }}{z^2}{\text{ }}-{\text{ }}xy{\text{ }}-{\text{ }}yz{\text{ }}-{\text{ }}zx} \right)\]

If,  $ x + y + z = 0 $ 

Then, \[{x^3}{\text{ }} + {\text{ }}{y^3}{\text{ }} + {\text{ }}{z^3}{\text{  =  }}3xyz{\text{ }}\]

Here,  $ \left( {x - y} \right) + \left( {y - z} \right) + \left( {z - x} \right) = 0 $ 

Therefore,  \[{\left( {x{\text{ }}-{\text{ }}y} \right)^3}{\text{ }} + {\text{ }}{\left( {y{\text{ }}-{\text{ }}z} \right)^3}{\text{ }} + {\text{ }}{\left( {z{\text{ }}-{\text{ }}x} \right)^3} = 3\left( {x - y} \right)\left( {y - z} \right)\left( {z - x} \right)\]

EXERCISE 2.3

1. Classify the following Polynomial as Polynomials in one variable, two variables etc.

(i)  $ {x^2} + x + 1 $ 

Ans: $ {x^2} + x + 1 $  is a Polynomial in one variable. 

(ii)  $ {y^3} - 5y $ 

Ans: $ {y^3} - 5y $  is a Polynomial in one variable.

(iii)  $ xy + yz + zx $ 

Ans: $ xy + yz + zx $  is a Polynomial in three variables.

(iv)  $ {x^2} - 2xy + {y^2} + 1 $ 

Ans: $ {x^2} - 2xy + {y^2} + 1 $  is a Polynomial in two variables.

2. Determine the degree of each of the following Polynomials:

(i)  $ 2x - 1 $ 

Ans: Since the highest power of x is  $ 1 $ , the degree of the Polynomial  $ 2x - 1 $  is  $ 1 $ .

(ii) $  - 10 $ 

Ans: $  - 10 $  is a non-zero constant. A constant term does not contain any variable and its degree is always 0.

(iii) $ {x^3} - 9x + 3{x^5} $ 

Ans: Since the highest power of x is  $ 5 $ , the degree of the Polynomial  $ {x^3} - 9x + 3{x^5} $  is  $ 5 $ .

(iv) $ {y^3}\left( {1 - {y^4}} \right) $ 

Ans: Here, we have $ {y^3}\left( {1 - {y^4}} \right) = {y^3} - {y^7} $ . Since the highest power of y is  $ 7 $ , the degree of the Polynomial is  $ 7 $ .

3. For the Polynomial  $ \dfrac{{{x^3} + 2x + 1}}{5} - \dfrac{7}{2}{x^2} - {x^6} $, write 

(i) the degree of the Polynomial 

Ans: $ \dfrac{{{x^3} + 2x + 1}}{5} - \dfrac{7}{2}{x^2} - {x^6} $ 

We can also write it as,

 $ \dfrac{{{x^3}}}{5} + \dfrac{2}{5}x + \dfrac{1}{5} - \dfrac{7}{2}{x^2} - {x^6} $ 

As we know that highest power of variable in a Polynomial is known as  degree of a Polynomial. In given Polynomial, the term with highest of x is  $  - {x^6} $ , and the exponent of x in this term in  $ 6 $ .

(ii) the coefficient of  $ {x^3} $ 

Ans: The coefficient of  $ {x^3} $ is  $ \dfrac{1}{5} $ .

(iii) the coefficient of  $ {x^6} $ 

Ans:  The coefficient of  $ {x^6} $  is  $  - 1 $ .

(iv) the constant term.

Ans: The constant term is  $ \dfrac{1}{5} $ .

4. Write the coefficient of  $ {x^2} $  in each of the following:

(i)  $ \dfrac{\pi }{6}x + {x^2} - 1 $ 

Ans: Coefficient of  $ {x^2} $  in the given Polynomial is  $ 1 $ .

(ii)  $ 3x - 5 $ 

Ans: The given Polynomial can also be written as  $ 0{x^2} + 3x - 5 $ . So, the coefficient of  $ {x^2} $  in the Polynomial is  $ 0 $ .

(iii)  $ \left( {x - 1} \right)\left( {3x - 4} \right) $ 

Ans: We can write the given polynomial as:

 $  \Rightarrow \left( {x - 1} \right)\left( {3x - 4} \right) $ 

 $  \Rightarrow 3{x^2} - 3x - 4x + 4 $ 

 $  \Rightarrow 3{x^2} - 7x + 4 $ 

Therefore, the coefficient of  $ {x^2} $  in the given Polynomial is  $ 3 $ .

(iv)  $ \left( {2x - 5} \right)\left( {2{x^2} - 3x + 1} \right) $ 

Ans: We can write the given polynomial as:

 $  \Rightarrow \left( {2x - 5} \right)\left( {2{x^2} - 3x + 1} \right) $ 

 $  \Rightarrow 4{x^3} - 6{x^2} + 2x - 10{x^2} + 15x - 5 $ 

 $  \Rightarrow 4{x^3} - 16{x^2} + 17x - 5 $ 

So, the coefficient of  $ {x^2} $  in the given Polynomial is – 16.

5. Classify the following as a constant, linear quadratic and cubic Polynomials:

(i)  $ 2 - {x^2} - {x^3} $ 

Ans: To do this question, we have to keep some points in mind:

(A) A Polynomial in which there is no variable term and there is only constant term, is known as a constant polynomial. 

(B) A Polynomial having degree 1 is known as a linear Polynomial. 

(C) A Polynomial of having degree 2 is known as quadratic Polynomial. 

(D) A Polynomial having degree 3 is known as cubic Polynomial. 

Cubic Polynomial is the correct answer.

(ii)  $ 3{x^3} $ 

Ans: Cubic Polynomial is the correct answer.

(iii)  $ 5t - \sqrt 7  $ 

Ans: Linear Polynomial is the correct answer.

(iv)  $ 4 - 5{y^2} $ 

Ans: Quadratic Polynomial is the correct answer.

(v)  $ 3 $ 

Ans: Constant Polynomial is the correct answer.

(vi)  $ 2 + x $ 

Ans: Linear Polynomial is the correct answer.

(vii)  $ {y^3} - y $ 

Ans: Cubic Polynomial is the correct answer.

(viii)  $ 1 + x + {x^3} $ 

Ans:  Cubic Polynomial is the correct answer.

(ix)  $ {t^2} $ 

Ans: Quadratic Polynomial is the correct answer.

(x)  $ \sqrt 2 x - 1 $ 

Ans: Linear Polynomial is the correct answer.

6. Give an example of a Polynomial, which is:

(i) monomial of degree  $ 1 $  

Ans: A Polynomial which contains  only one term is called a monomial, a Polynomial having only two terms is called binomial, a Polynomial having only three terms is called a trinomial.

$ 5x $  is monomial of degree  $ 1 $ .

(ii) binomial of degree  $ 20 $  

Ans: $ {x^{20}} + 5 $  is a binomial of degree  $ 20 $ . 

(iii) trinomial of degree  $ 2 $ 

Ans: $2{x^2} + 2x + 1 $  is a trinomial of degree  $ 2 $ .

7. Find the value of the Polynomial  $ 3{x^3} - 4{x^2} + 7x + 5 $ , when  $ x = 3 $  and also when  $ x =  - 3 $ .

Ans: Let p(x) be the given Polynomial.

 $ p\left( x \right) = 3{x^2} - 4{x^2} + 7x - 5 $ 

Now, put  $ x = 3 $ 

 $ p\left( 3 \right) = 3{\left( 3 \right)^3} - 4{\left( 3 \right)^2} + 7\left( 3 \right) - 5 $ 

 $ p\left( 3 \right) = 3\left( {27} \right) - 4\left( 9 \right) + 7\left( 3 \right) - 5 $ 

 $ p\left( 3 \right) = 61 $ 

Now,

Put  $ x =  - 3 $ 

 $ p\left( { - 3} \right) = 3{\left( { - 3} \right)^3} - 4{\left( { - 3} \right)^2} + 7\left( { - 3} \right) - 5 $ 

 $ p\left( { - 3} \right) = 3\left( { - 27} \right) - 4\left( 9 \right) + 7\left( { - 3} \right) - 5 $ 

 $ p\left( { - 3} \right) =  - 81 - 36 - 21 - 5 $ 

 $ p\left( { - 3} \right) =  - 143 $ 

8. If  $ p\left( x \right) = {x^2} - 4x + 3 $ , evaluate  $ p\left( 2 \right) - p\left( { - 1} \right) + p\left( {\dfrac{1}{2}} \right) $ 

Ans: We have  $ p\left( x \right) = {x^2} - 4x + 3 $ 

Now, put  $ x = 2 $ 

 $ p\left( 2 \right) = \left( {{2^2} - 4 \times 2 + 3} \right) = \left( {4 - 8 + 3} \right) = \left( { - 4 + 3} \right) =  - 1 $ 

Now, put  $ x =  - 1 $ 

 $ p\left( { - 1} \right) = \left( {{{\left( { - 1} \right)}^2} - 4 \times \left( { - 1} \right) + 3} \right) = \left( {1 + 4 + 3} \right) = 8 $ 

Now, put  $ x = \dfrac{1}{2} $ 

 $ p\left( {\dfrac{1}{2}} \right) = \left( {{{\left( {\dfrac{1}{2}} \right)}^2} - 4 \times \dfrac{1}{2} + 3} \right) = \left( {\dfrac{1}{4} - 2 + 3} \right) = \left( {1 + \dfrac{1}{4}} \right) = \dfrac{5}{4} $ 

Now,

 $ p\left( 2 \right) - p\left( { - 1} \right) + p\left( {\dfrac{1}{2}} \right) =  - 1 - 8 + \dfrac{5}{4} $ 

 $ p\left( 2 \right) - p\left( { - 1} \right) + p\left( {\dfrac{1}{2}} \right) =  - 9 + \dfrac{5}{4} = \dfrac{{ - 36 + 5}}{4} =  - \dfrac{{31}}{4} $ 

9. Find  $ p\left( 0 \right) $  ,  $ p\left( 1 \right) $  ,  $ p\left( { - 2} \right) $  for the following Polynomials:

(i)  $ p\left( x \right) = 10x - 4{x^2} - 3 $

Ans: We have

 $ p\left( x \right) = 10x - 4{x^2} - 3 $ 

Put,  $ x = 0 $ 

 $ p\left( 0 \right) = 10\left( 0 \right) - 4{\left( 0 \right)^2} - 3 =  - 3 $ 

Put,  $ x = 1 $ 

 $ p\left( 1 \right) = 10\left( 1 \right) - 4{\left( 1 \right)^2} - 3 = 10 - 4 - 3 = 3 $ 

Put,  $ x =  - 2 $ 

 $ p\left( { - 2} \right) = 10\left( { - 2} \right) - 4{\left( { - 2} \right)^2} - 3 =  - 20 - 16 - 3 =  - 39 $ 

(ii)  $ p\left( y \right) = \left( {y + 2} \right)\left( {y - 2} \right) $ 

Ans: We have

 $ p\left( y \right) = \left( {y + 2} \right)\left( {y - 2} \right) $ 

Put,  $ y = 0 $ 

 $ p\left( 0 \right) = \left( {0 + 2} \right)\left( {0 - 2} \right) =  - 4 $ 

Put,  $ y = 1 $ 

 $ p\left( 1 \right) = \left( {1 + 2} \right)\left( {1 - 2} \right) = \left( 3 \right)\left( { - 1} \right) =  - 3 $ 

Put,  $ y =  - 2 $ 

 $ p\left( { - 2} \right) = \left( { - 2 + 2} \right)\left( { - 2 - 2} \right) = 0 $ 

10. Verify whether the following are true or false. 

(i)  $  - 3 $  is a zero of  $ x - 3 $ . 

Ans: A number c can be a zero of a Polynomial p(x) if a number c is such that \[p\left( c \right){\text{ }} = {\text{ }}0\].

 Let  $ p\left( x \right) = x - 3 $ 

 $ p\left( { - 3} \right) =  - 3 - 3 =  - 6 $ 

 $ p\left( { - 3} \right) \ne 0 $ 

Hence,  $  - 3 $  is not a zero of  $ x - 3 $  .

So, the result is False.

(ii)  $  - \dfrac{1}{3} $  is a zero of  $ 3x + 1 $ . 

Ans: A number c can be a zero of a Polynomial p(x) if a number c is such that \[p\left( c \right){\text{ }} = {\text{ }}0\].

Let  $ p\left( x \right) = 3x + 1 $ 

Put,  $ x =  - \dfrac{1}{3} $ 

 $ p\left( { - \dfrac{1}{3}} \right) = 3\left( { - \dfrac{1}{3}} \right) + 1 $ 

 $ p\left( { - \dfrac{1}{3}} \right) =  - 1 + 1 = 0 $ 

Hence,  $  - \dfrac{1}{3} $  is zero of  $ p\left( x \right) = 3x + 1 $ .

So, the result is True.

(iii)  $  - \dfrac{4}{5} $  is a zero of  $ 4 - 5y $ . 

Ans: A number c can be a zero of a Polynomial p(x) if a number c is such that \[p\left( c \right){\text{ }} = {\text{ }}0\].

Let  $ p\left( y \right) = 4 - 5(y) $ 

Put,  $ y =  - \dfrac{4}{5} $ 

 $ p\left( { - \dfrac{4}{5}} \right) = 4 - 5\left( { - \dfrac{4}{5}} \right) $ 

 $ p\left( { - \dfrac{4}{5}} \right) = 4 + 4 = 8 $ 

Hence,  $  - \dfrac{4}{5} $  is zero of  $ p\left( y \right) = 4 - 5(y) $ .

(iv)  $ 0 $  and  $ 2 $  are the zeroes of  $ {t^2} - 2t $ 

Ans: Let  $ p\left( t \right) = {t^2} - 2t $ 

Put, $ t = 0 $ 

 $ p\left( 0 \right) = {\left( 0 \right)^2} - 2\left( 0 \right) $ 

 $ p\left( 0 \right) = 0 $ 

Put, $ t = 2 $ 

 $ p\left( 2 \right) = {\left( 2 \right)^2} - 2\left( 2 \right) = 4 - 4 = 0 $ 

Hence,  $ 0 $  and  $ 2 $  are zeroes of the Polynomial  $ {t^2} - 2t $ .

So, the result is True.

(v)   $  - 3 $  is a zero  $ {y^2} + y - 6 $ 

Ans: Let  $ p\left( y \right) = {y^2} + y - 6 $ 

Put,  $ y =  - 3 $ 

 $ p\left( { - 3} \right) = {\left( { - 3} \right)^2} + \left( { - 3} \right) - 6 $ 

 $ p\left( { - 3} \right) = 9 - 9 = 0 $ 

Hence,  $  - 3 $   is a zero of the Polynomial  $ {y^2} + y - 6 $ .

So, the result is True.

11.  Find the zeroes of the Polynomial in each of the following:

(i)  $ p\left( x \right) = x - 4 $ 

Ans: Here we have to Solve the equation  $ p\left( x \right) = 0 $ , we get

 $ x - 4 = 0 $ 

 $ x = 4 $  

So,  $ 4 $  is a zero of the Polynomial  $ x - 4 $ .

(ii)  $ g\left( x \right) = 3 - 6x $ 

Ans: Here we have to Solve the equation  $ g\left( x \right) = 0 $ , we get

 $ 3 - 6x = 0 $ 

 $ x = \dfrac{1}{2} $  

So,  $ \dfrac{1}{2} $  is a zero of the Polynomial  $ 3 - 6x $ .

(iii)  $ q\left( x \right) = 2x - 7 $ 

Ans: Here we have to Solve the equation  $ q\left( x \right) = 0 $ , we get

 $ 2x - 7 = 0 $ 

 $ x = \dfrac{7}{2} $  

So,  $ \dfrac{7}{2} $  is a zero of the Polynomial  $ 2x - 7 $ .

(iv)  $ h\left( y \right) = 2y $ 

Ans: Here we have to Solve the equation  $ h\left( y \right) = 0 $ , we get

 $ 2y = 0 $ 

 $ y = 0 $  

So,  $ 0 $  is a zero of the Polynomial  $ 2y $ .

12. Find the zeroes of the Polynomial  $ {\left( {x - 2} \right)^2} - {\left( {x + 2} \right)^2} $ .

Ans: Let  $ p\left( x \right) = {\left( {x - 2} \right)^2} - {\left( {x + 2} \right)^2} $ 

To get the zeroes of p(x), we have to Solve the equation \[p\left( x \right){\text{ }} = {\text{ }}0\].

So, \[p\left( x \right){\text{ }} = {\text{ }}0\]

 $ {\left( {x - 2} \right)^2} - {\left( {x + 2} \right)^2} = 0 $ 

 $ \left( {\left( {x - 2} \right) - \left( {x + 2} \right)} \right)\left( {\left( {x - 2} \right) + \left( {x + 2} \right)} \right) = 0 $ 

\[\left( { - 4} \right)\left( {2x} \right) = 0\]

 $ x = 0 $ 

Hence,  $ x = 0 $  is the only one zero of  $ p\left( x \right) $ .

13. By acute division, find the quotient and the remainder when the first Polynomial is divided by the second  $ {x^4} + 1\,;\,x + 1 $ .

Ans: By acute division, we have

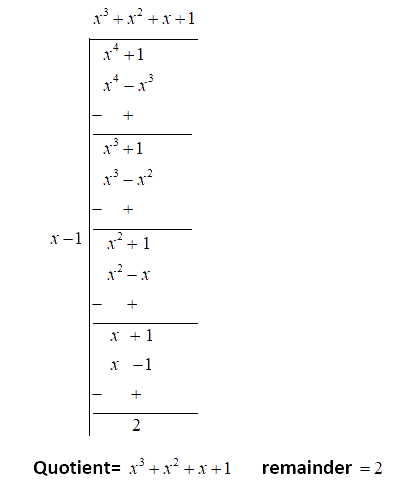
14. By remainder Theorem find the remainder, when p(x) is divided by g(x), where

(i)  $ p\left( x \right) = {x^3} - 2{x^2} - 4x - 1\,,\,g\left( x \right) = x + 1 $ 

Ans:  According to the remainder theorem, if we divide a polynomial p(x) by a factor \[\left( {{\text{ }}{\mathbf{x}}{\text{ }}-{\text{ }}{\mathbf{a}}{\text{ }}} \right)\]; then you will find a smaller polynomial with a remainder. This remainder which has been obtained is actually a value of p(x) at  $ x = a $ , specifically p(a). So, \[\left( {{\text{ }}{\mathbf{x}}{\text{ }}-{\text{ }}{\mathbf{a}}{\text{ }}} \right)\] is the divisor of p(x) if and only if \[p\left( a \right){\text{ }} = {\text{ }}0\] .

We have,  $ g\left( x \right) = x + 1 $ 

Now, put 

\[g\left( x \right) = 0\]

Therefore,

 $  \Rightarrow x + 1 = 0 $ 

  $  \Rightarrow x =  - 1 $ 

Remainder  $  = \,p\left( { - 1} \right) $ 

 $  = {\left( { - 1} \right)^3} - 2{\left( { - 1} \right)^2} - 4\left( { - 1} \right) =  - 1 - 2 + 4 - 1 = 0 $ 

(ii)  $ p\left( x \right) = {x^3} - 3{x^2} + 4x + 50\,,\,g\left( x \right) = x - 3 $ 

Ans: According to the remainder theorem, if we divide a polynomial p(x) by a factor \[\left( {{\text{ }}{\mathbf{x}}{\text{ }}-{\text{ }}{\mathbf{a}}{\text{ }}} \right)\]; then you will find a smaller polynomial with a remainder. This remainder which has been obtained is actually a value of p(x) at  $ x = a $ , specifically p(a). So, \[\left( {{\text{ }}{\mathbf{x}}{\text{ }}-{\text{ }}{\mathbf{a}}{\text{ }}} \right)\] is the divisor of p(x) if and only if \[p\left( a \right){\text{ }} = {\text{ }}0\] .

We have,  $ g\left( x \right) = x - 3 $ 

Therefore,

 $  \Rightarrow x - 3 = 0 $ 

  $  \Rightarrow x = 3 $ 

Remainder  $  = \,p\left( 3 \right) $ 

 $  = {\left( 3 \right)^3} - 3{\left( 3 \right)^2} + 4\left( 3 \right) + 50 = 27 - 27 + 12 + 50 = 62 $ 

(iii)  $ p\left( x \right) = 4{x^3} - 12{x^2} + 14x - 3\,,\,g\left( x \right) = 2x - 1 $ 

Ans: According to the remainder theorem, if we divide a polynomial p(x) by a factor \[\left( {{\text{ }}{\mathbf{x}}{\text{ }}-{\text{ }}{\mathbf{a}}{\text{ }}} \right)\]; then you will find a smaller polynomial with a remainder. This remainder which has been obtained is actually a value of p(x) at  $ x = a $ , specifically p(a). So, \[\left( {{\text{ }}{\mathbf{x}}{\text{ }}-{\text{ }}{\mathbf{a}}{\text{ }}} \right)\] is the divisor of p(x) if and only if \[p\left( a \right){\text{ }} = {\text{ }}0\] .

We have,  $ g\left( x \right) = 2x - 1 $ 

Therefore,

 $  \Rightarrow 2x - 1 = 0 $ 

  $  \Rightarrow x = \dfrac{1}{2} $ 

Remainder  $  = \,p\left( {\dfrac{1}{2}} \right) $ 

 $  = 4{\left( {\dfrac{1}{2}} \right)^3} - 12{\left( {\dfrac{1}{2}} \right)^2} + 14\left( {\dfrac{1}{2}} \right) - 3 = 4\left( {\dfrac{1}{8}} \right) - 12\left( {\dfrac{1}{4}} \right) + 7 - 3 $ 

 $  = \dfrac{1}{2} - 3 + 7 - 3 = \dfrac{1}{2} + 1 = \dfrac{3}{2} $ 

(iv)  $ p\left( x \right) = {x^3} - 6{x^2} + 2x - 4\,,\,g\left( x \right) = 1 - \dfrac{3}{2}x $ 

Ans: According to the remainder theorem, if we divide a polynomial p(x) by a factor \[\left( {{\text{ }}{\mathbf{x}}{\text{ }}-{\text{ }}{\mathbf{a}}{\text{ }}} \right)\]; then you will find a smaller polynomial with a remainder. This remainder which has been obtained is actually a value of p(x) at  $ x = a $ , specifically p(a). So, \[\left( {{\text{ }}{\mathbf{x}}{\text{ }}-{\text{ }}{\mathbf{a}}{\text{ }}} \right)\] is the divisor of p(x) if and only if \[p\left( a \right){\text{ }} = {\text{ }}0\] .

 We have,  $ g\left( x \right) = 1 - \dfrac{3}{2}x $ 

Therefore,

 $  \Rightarrow 1 - \dfrac{3}{2}x = 0 $ 

  $  \Rightarrow x = \dfrac{2}{3} $ 

Remainder  $  = \,p\left( {\dfrac{2}{3}} \right) $ 

 $  = {\left( {\dfrac{2}{3}} \right)^3} - 6{\left( {\dfrac{2}{3}} \right)^2} + 2\left( {\dfrac{2}{3}} \right) - 4\, = \dfrac{8}{{27}} - 6 \times \dfrac{4}{9} + \dfrac{4}{3} - 4 $ 

 $  = \dfrac{8}{{27}} - \dfrac{8}{3} + \dfrac{4}{3} - 4 = \dfrac{{8 - 72 + 36 - 108}}{{27}} = \dfrac{{ - 136}}{{27}} $ 

15. Check whether p(x) is a multiple of g(x) or not:

(i)  $ p\left( x \right) = {x^3} - 5{x^2} + 4x - 3\,,\,g\left( x \right) = x - 2 $ 

Ans: According to the remainder theorem, if we divide a polynomial p(x) by a factor \[\left( {{\text{ }}{\mathbf{x}}{\text{ }}-{\text{ }}{\mathbf{a}}{\text{ }}} \right)\]; then you will find a smaller polynomial with a remainder. This remainder which has been obtained is actually a value of p(x) at  $ x = a $ , specifically p(a). So, \[\left( {{\text{ }}{\mathbf{x}}{\text{ }}-{\text{ }}{\mathbf{a}}{\text{ }}} \right)\] is the divisor of p(x) if and only if \[p\left( a \right){\text{ }} = {\text{ }}0\] .

p(x) is a multiple of g(x) if g(x) divides p(x)

Now,  $ g\left( x \right) = x - 2 $  gives  $ x = 2 $ if we put  $ g\left( x \right) = 0 $ .

Remainder  $  = \,p\left( 2 \right) = {\left( 2 \right)^3} - 5{\left( 2 \right)^2} + 4\left( 2 \right) - 3 $ 

 $  = 8 - 5\left( 4 \right) + 8 - 3 = 8 - 20 + 8 - 3 =  - 7 $ 

Hence, the remainder  $  \ne 0 $ 

Therefore, function p(x) is not a multiple of function g(x).

(ii)  $ p\left( x \right) = 2{x^3} - 11{x^2} - 4x + 5\,,\,g\left( x \right) = 2x + 1 $ 

Ans: According to the remainder theorem, if we divide a polynomial p(x) by a factor \[\left( {{\text{ }}{\mathbf{x}}{\text{ }}-{\text{ }}{\mathbf{a}}{\text{ }}} \right)\]; then you will find a smaller polynomial with a remainder. This remainder which has been obtained is actually a value of p(x) at  $ x = a $ , specifically p(a). So, \[\left( {{\text{ }}{\mathbf{x}}{\text{ }}-{\text{ }}{\mathbf{a}}{\text{ }}} \right)\] is the divisor of p(x) if and only if \[p\left( a \right){\text{ }} = {\text{ }}0\] .

p(x) will be a multiple of g(x) if and only if g(x) divides p(x).

so,

 $ g\left( x \right) = 2x + 1 $  give  $ x =  - \dfrac{1}{2} $ 

remainder  $  = p\left( { - \dfrac{1}{2}} \right) = 2{\left( {\dfrac{{ - 1}}{2}} \right)^3} - 11{\left( { - \dfrac{1}{2}} \right)^2} - 4\left( { - \dfrac{1}{2}} \right) + 5 $ 

 $  = 2\left( { - \dfrac{1}{8}} \right) - 11\left( {\dfrac{1}{4}} \right) + 2 + 5 = \dfrac{{ - 1}}{4} - \dfrac{{11}}{4} + 7 $ 

 $  = \dfrac{{ - 1 - 11 + 28}}{4} = \dfrac{{16}}{4} = 4 $ 

Since the remainder  $  \ne 0 $ .

So, p(x) will not be a multiple of g(x).

16. Show that:

(i)  $ x + 3 $  is a factor of  $ 69 + 11x - {x^2} + {x^3} $ 

Ans: Let  $ p\left( x \right) = 69 + 11x - {x^2} + {x^3}\,\,,\,\,g\left( x \right) = x + 3 $ 

 $ g\left( x \right) = x + 3 = 0 $ 

It will give,  $ x =  - 3 $ 

g(x) will be a factor of p(x) if  $ p\left( { - 3} \right) = 0 $  (Factor theorem).

Now,  $ p\left( { - 3} \right) = 69 + 11\left( { - 3} \right) - {\left( { - 3} \right)^2} + {\left( { - 3} \right)^3} $ 

 $  = 69 - 33 - 9 - 27 = 0 $ 

Hence  $ p\left( { - 3} \right) = 0 $ ,  g(x) will be a factor of p(x).

(ii)  $ 2x - 3 $  is a factor of  $ x + 2{x^3} - 9{x^2} + 12 $ 

Ans: Let  $ p\left( x \right) = x + 2{x^3} - 9{x^2} + 12 $  and  $ g\left( x \right) = 2x - 3 $ 

 $ g\left( x \right) = 2x - 3 $  

Now,

 $ g\left( x \right) = 0 $ 

 $ 2x - 3 = 0 $ 

 $ x = \dfrac{3}{2} $ , 

g(x) will be factor of p(x) if  $ p\left( {\dfrac{3}{2}} \right) = 0 $  (Factor theorem)

Now,  $ p\left( {\dfrac{3}{2}} \right) = \dfrac{3}{2} + 2{\left( {\dfrac{3}{2}} \right)^3} - 9{\left( {\dfrac{3}{2}} \right)^2} + 12 = \dfrac{3}{2} + 2\left( {\dfrac{{27}}{8}} \right) - 9\left( {\dfrac{9}{4}} \right) + 12 $ 

 $  = \dfrac{3}{2} + \dfrac{{27}}{4} - \dfrac{{81}}{4} + 12 = \dfrac{{6 + 27 - 81 + 48}}{4} = \dfrac{0}{4} = 0 $ 

Since,  $ p\left( {\dfrac{3}{2}} \right) = 0 $ , therefore, g(x) is a factor of p(x).

17. Determine which of the following Polynomials has  $ x - 2 $ the factor as:

(i)  $ 3{x^2} + 6x - 24 $ 

Ans: As we know that if  $ \left( {x - a} \right) $ is a factor of p(x), then p(A) =0.

Let  $ p\left( x \right) = 3{x^2} + 6x - 24 $ 

If  $ x - 2 $  will be factor of  $ p\left( x \right) = 3{x^2} + 6x - 24 $ , then  $ p\left( 2 \right) $  should be equal to  $ 0 $ .

Now,  $ p\left( 2 \right) = 3{\left( 2 \right)^2} + 6\left( 2 \right) - 24 $ 

 $  = 3\left( 4 \right) + 6\left( 2 \right) - 24 = 12 + 12 - 24 = 0 $ 

Therefore, by factor theorem  $ x - 2 $ , is factor of  $ 3{x^2} + 6x - 24 $ .

(ii)  $ 4{x^2} + x - 2 $

Ans: As we know that if  $ \left( {x - a} \right) $ is a factor of p(x), then p(A) =0.

Let  $ p\left( x \right) = 4{x^2} + x - 2 $ 

If  $ x - 2 $  will be factor of  $ p\left( x \right) = 4{x^2} + x - 2 $ , then  $ p\left( 2 \right) $  should be equal to  $ 0 $ .

Now, 

 $ p\left( 2 \right) = 4{\left( 2 \right)^2} + 2 - 2 $ 

 $  = 16 + 2 - 2 = 16 $ 

Since,  $ 16 \ne 0 $ 

Therefore,  $ x - 2 $  is not a factor of  $ 4{x^2} + x - 2 $ .

18. Show that  $ p - 1 $  is a factor of  $ {p^{10}} - 1 $  and also of  $ {p^{11}} - 1 $ .

Ans:  $ p - 1 $  is a factor  $ {p^{10}} - 1 $ , then  $ {\left( 1 \right)^{10}} - 1 $ should be equal to zero.

Now,  $ {\left( 1 \right)^{10}} - 1 = 1 - 1 = 0 $ 

Therefore,  $ p - 1 $  is a factor  $ {p^{10}} - 1 $ .

Again, if  $ p - 1 $  is a factor of  $ {p^{11}} - 1 $  , then  $ {\left( 1 \right)^{11}} - 1 $  should be equal to zero.

Now,  $ {\left( 1 \right)^{11}} - 1 = 1 - 1 = 0 $ 

Therefore,  $ p - 1 $ is a factor  $ {p^{11}} - 1 $ .

Hence,  $ p - 1 $  is a factor of  $ {p^{10}} - 1 $  and also of  $ {p^{11}} - 1 $ .

19. For what value of m is  $ {x^3} - 2m{x^2} + 16 $  divisible by  $ x + 2 $ ?

Ans: If  $ {x^3} - 2m{x^2} + 16 $  is divisible by  $ x + 2 $  , then  $ x + 2 $  is a factor of  $ {x^3} - 2m{x^2} + 16 $ .

Now, let  $ p\left( x \right) = {x^3} - 2m{x^2} + 16 $ 

As,  $ x + 2 = x - \left( { - 2} \right) $  is a factor of  $ {x^3} - 2m{x^2} + 16 $ .

So,  $ p\left( { - 2} \right) = 0 $ 

Now,  $ p\left( { - 2} \right) = {\left( { - 2} \right)^3} - 2m{\left( { - 2} \right)^2} + 16 $ 

 $  =  - 8 - 8m + 16 = 8 - 8m $ 

Now,  $ p\left( { - 2} \right) = 0 $ 

 $  \Rightarrow \,8 - 8m = 0 $ 

 $  \Rightarrow 8m = 8 $ 

 $  \Rightarrow m = 1 $ 

Hence, for  $ m = 1 $  ,  $ x + 2 $  is a factor of  $ {x^3} - 2m{x^2} + 16 $ so that  $ {x^3} - 2m{x^2} + 16 $  is completely divisible by  $ x + 2 $ .

20. If  $ x + 2a $  is a factor of  $ {x^5} - 4{a^2}{x^3} + 2x + 2a + 3 $ , find a.

Ans: Let  $ p\left( x \right) = {x^5} - 4{a^2}{x^3} + 2x + 2a + 3 $ 

If  $ x - \left( { - 2a} \right) $  is a factor of  $ p(x) $ , then  $ p\left( { - 2a} \right) = 0 $ .

 $ p\left( { - 2a} \right) = {\left( { - 2a} \right)^5} - 4{a^2}{\left( { - 2a} \right)^3} + 2\left( { - 2a} \right) + 2a + 3 $ 

 $  =  - 32{a^5} + 32{a^5} - 4a + 2a + 3 $ 

 $  =  - 2a + 3 $ 

Now,  $ p\left( { - 2a} \right) = 0 $ 

 $  \Rightarrow  - 2a + 3 = 0 $ 

 $  \Rightarrow a = \dfrac{3}{2} $ 

21. Find the value of m so that  $ 2x - 1 $  be a factor of  $ 8{x^4} + 4{x^3} - 16{x^2} + 10x + m $ .

Ans: Let  $ p\left( x \right) = 8{x^4} + 4{x^3} - 16{x^2} + 10x + m $ 

As,  $ \left( {2x - 1} \right) $  is a factor of  $ p\left( x \right) $ .

Then  $ p\left( {\dfrac{1}{2}} \right) = 0 $ (using factor theorem)

 $  \Rightarrow 8{\left( {\dfrac{1}{2}} \right)^4} + 4{\left( {\dfrac{1}{2}} \right)^3} - 16{\left( {\dfrac{1}{2}} \right)^2} + 10\left( {\dfrac{1}{2}} \right) + m = 0 $ 

 $  \Rightarrow 8\left( {\dfrac{1}{{16}}} \right) + 4\left( {\dfrac{1}{8}} \right) - 16\left( {\dfrac{1}{4}} \right) + 5 + m = 0 $ 

 $  \Rightarrow \dfrac{1}{2} + \dfrac{1}{2} - 4 + 5 + m = 0 $ 

 $  \Rightarrow 1 + 1 + m = 0 $ 

 $  \Rightarrow \,m =  - 2 $ 

22. If  $ x + 1 $  is a factor of  $ a{x^3} + {x^2} - 2x + 4a - 9 $ , find the value of a.

Ans: Let  $ p\left( x \right) = a{x^3} + {x^2} - 2x + 4a - 9 $ 

As  $ x + 1 $  is a factor of p(x)

Then,

 $ p\left( { - 1} \right) = 0 $  (By factor theorem)

 $  \Rightarrow \,a{\left( { - 1} \right)^3} + {\left( { - 1} \right)^2} - 2\left( { - 1} \right) + 4a - 9 = 0 $ 

 $  \Rightarrow \, - a + 1 + 2 + 4a - 9 = 0 $ 

 $  \Rightarrow \,3a - 6 = 0 $ 

 $  \Rightarrow \,3a = 6 $ 

 $  \Rightarrow \,a = 2 $ 

23. Factorize:

(i)  $ {x^2} + 9x + 18 $ 

Ans: In order to factorize  $ {x^2} + 9x + 18 $ , we have to split the middle term.

 $  \Rightarrow {x^2} + 9x + 18 $ 

 $  \Rightarrow {x^2} + \left( {6 + 3} \right)x + 18 $ 

 $  \Rightarrow {x^2} + 6x + 3x + 18 $ 

 $  \Rightarrow x\left( {x + 6} \right) + 3\left( {x + 6} \right) $ 

 $  \Rightarrow \left( {x + 3} \right)\left( {x + 6} \right) $ 

(ii)  $ 6{x^2} + 7x - 3 $ 

Ans: In order to factorize  $ 6{x^2} + 7x - 3 $ , we have to split the middle term.

 $  \Rightarrow 6{x^2} + 7x - 3 $ 

 $  \Rightarrow 6{x^2} + \left( {9 - 2} \right)x - 3 $ 

 $  \Rightarrow 6{x^2} + 9x - 2x - 3 $ 

 $  \Rightarrow 3x\left( {2x + 3} \right) - 1\left( {2x + 3} \right) $ 

 $  \Rightarrow \left( {3x - 1} \right)\left( {2x + 3} \right) $ 

(iii)  $ 2{x^2} - 7x - 15 $ 

Ans:  If we want to factorise  $ 2{x^2} - 7x - 15 $ , we have to split the middle term.

 $  \Rightarrow 2{x^2} - 7x - 15 $ 

 $  \Rightarrow 2{x^2} - \left( {10 - 3} \right)x - 15 $ 

 $  \Rightarrow 2{x^2} - 10x + 3x - 15 $ 

 $  \Rightarrow 2x\left( {x - 5} \right) + 3\left( {x - 5} \right) $ 

 $  \Rightarrow \left( {2x + 3} \right)\left( {x - 5} \right) $ 

(iv)  $ 84 - 2r - 2{r^2} $ 

Ans: If we want to factorise  $ 84 - 2r - 2{r^2} $ , we have to split the middle term.

 $  \Rightarrow  - \left( {2{r^2} + 2r - 84} \right) $ 

 $  \Rightarrow  - 2\left( {{r^2} + r - 42} \right) $ 

 $  \Rightarrow  - 2\left( {{r^2} + \left( {7 - 6} \right)r - 42} \right) $ 

 $  \Rightarrow  - 2\left( {{r^2} + 7r - 6r - 42} \right) $ 

 $  \Rightarrow  - 2\left( {r\left( {r + 7} \right) - 6\left( {r + 7} \right)} \right) $ 

 $  \Rightarrow 2\left( {6 - r} \right)\left( {r + 7} \right) $ 

24. Factorise:

(i)  $ 2{x^3} - 3{x^2} - 17x + 30 $ 

Ans: Let  $ f\left( x \right) = 2{x^3} - 3{x^2} - 17x + 30 $  be the given Polynomial. The factors of the constant term  $  + 30 $  are  $  \pm 1, \pm 2, \pm 3, \pm 5, \pm 6, \pm 10, \pm 15, \pm 30 $  . The factor of coefficient of  $ {x^3} $  is  $ 2 $ .

Therefore, possible rational roots of f(x) are:

 $  \Rightarrow  \pm 1, \pm 3, \pm 5, \pm 15, \pm \dfrac{1}{2}, \pm \dfrac{3}{2}, \pm \dfrac{5}{2}, \pm \dfrac{{15}}{2} $ 

We  $ f\left( 2 \right) = 2{\left( 2 \right)^3} - 3{\left( 2 \right)^2} - 17\left( 2 \right) + 30 $ 

 $  = 2\left( 8 \right) - 3\left( 4 \right) - 17\left( 2 \right) + 30 $ 

 $  = 16 - 12 - 34 + 30 = 0 $ 

And  $ f\left( { - 3} \right) = 2{\left( { - 3} \right)^3} - 3{\left( { - 3} \right)^2} - 17\left( { - 3} \right) + 30 $ 

 $  = 2\left( { - 27} \right) - 3\left( 9 \right) - 17\left( { - 3} \right) + 30 $ 

 $  =  - 54 - 27 + 51 + 30 = 0 $ 

Hence,  $ \left( {x - 2} \right) $   $ \left( {x + 3} \right) $ ,  will be the factors of  $ f\left( x \right) $ .

 $  \Rightarrow {x^2} + x - 6 $  is a factor of 

 $ f\left( x \right) $ .

Let's divide  $ f\left( x \right) = 2{x^3} - 3{x^2} - 17x + 30 $  by  $ {x^2} + x - 6 $  to get the other factors of  $ f\left( x \right) $ .

Factors of  $ f\left( x \right) $ .

By long division, we have 

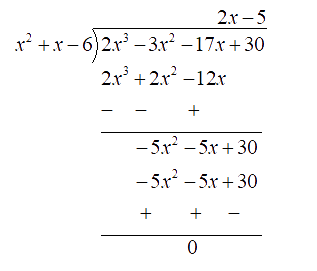
 $ 2{x^3} - 3{x^2} - 17x + 30 = \left( {{x^2} + x - 6} \right)\left( {2x - 5} \right) $ 

 $  \Rightarrow \,2{x^3} - 3{x^2} - 17x + 30 = \left( {x - 2} \right)\left( {x + 3} \right)\left( {2x - 5} \right) $ 

Hence,  $ \,2{x^3} - 3{x^2} - 17x + 30 = \left( {x - 2} \right)\left( {x + 3} \right)\left( {2x - 5} \right) $ 

(ii)  $ {x^3} - 6{x^2} + 11x - 6 $ 

Ans: Let  $ f\left( x \right) = {x^3} - 6{x^2} + 11x - 6 $ be the given Polynomial. The factors of the constant term  $  - 6 $  are  $  \pm 1, \pm 2, \pm 3\,\,and\,\, \pm 6 $ . 

We  $ f\left( 1 \right) = {\left( 1 \right)^3} - 6{\left( 1 \right)^2} + 11\left( 1 \right) - 6 = 0 $ 

And  $ f\left( 2 \right) = {\left( 2 \right)^3} - 6{\left( 2 \right)^2} + 11\left( 2 \right) - 6 = 8 - 24 + 22 - 6 = 0 $ 

Hence,  $ \left( {x - 1} \right) $   $ \left( {x - 2} \right) $ ,  will be factors   $ f\left( x \right) $ .

 $  \Rightarrow \left( {x - 1} \right)\left( {x - 2} \right) = {x^2} - 3x + 2 $  will be a factor of  $ f\left( x \right) $ .

Let us divide  $ f\left( x \right) = {x^3} - 6{x^2} + 11x - 6 $  by  $ {x^2} - 3x + 2 $  to get the other factors of  $ f\left( x \right) $ .

Factors of  $ f\left( x \right) $ .

By long division, we have 

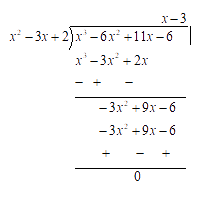
 $ {x^3} - 6{x^2} + 11x - 6 = \left( {{x^2} - 3x + 2} \right)\left( {x - 3} \right) $ 

 $  \Rightarrow {x^3} - 6{x^2} + 11x - 6 = \left( {x - 1} \right)\left( {x - 2} \right)\left( {x - 3} \right) $ 

Hence,  $ {x^3} - 6{x^2} + 11x - 6 = \left( {x - 1} \right)\left( {x - 2} \right)\left( {x - 3} \right) $ 

(iii)  $ {x^3} + {x^2} - 4x + 4 $ 

Ans: Let  $ f\left( x \right) = {x^3} + {x^2} - 4x - 4 $ be the given Polynomial. The factors of the constant term  $  - 4 $  are  $  \pm 1, \pm 2, \pm 4\, $ . 

We  $ f\left( { - 1} \right) = {\left( { - 1} \right)^3} + {\left( { - 1} \right)^2} - 4\left( { - 1} \right) - 4 = 0 $ 

And  $ f\left( 2 \right) = {\left( 2 \right)^3} + {\left( 2 \right)^2} - 4\left( 2 \right) - 4 = 8 + 4 - 8 - 4 = 0 $ 

Hence,  $ \left( {x + 1} \right) $  ,  $ \left( {x - 2} \right) $  are factors of  $ f\left( x \right) $ .

 $  \Rightarrow \left( {x + 1} \right)\left( {x - 2} \right) = {x^2} - x - 2 $  will be a factor of  $ f\left( x \right) $ .

Let's now divide  $ f\left( x \right) = {x^3} + {x^2} - 4x - 4 $  by  $ {x^2} - x - 2 $  to get the other factors of  $ f\left( x \right) $ .

By long division, we have 

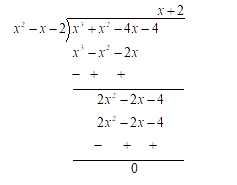
 $ {x^3} + {x^2} - 4x - 4 = \left( {{x^2} - x - 2} \right)\left( {x + 2} \right) $ 

 $  \Rightarrow {x^3} + {x^2} - 4x - 4 = \left( {x + 1} \right)\left( {x - 2} \right)\left( {x + 2} \right) $ 

Hence,  $ {x^3} + {x^2} - 4x - 4 = \left( {x + 1} \right)\left( {x - 2} \right)\left( {x + 2} \right) $ 

(iv)  $ 3{x^3} - {x^2} - 3x + 1 $ 

Ans: Let  $ f\left( x \right) = 3{x^3} - {x^2} - 3x + 1 $ be the given Polynomial. The factors of a constant term  $  + 1 $  are  $  \pm 1.\, $ The factor of coefficient of  $ {x^3} $  is  $ 3 $ .Hence, possible rational roots of  $ f\left( x \right) $  are  $  \pm \dfrac{1}{3} $ . 

We have,

 $ f\left( 1 \right) = 3{\left( 1 \right)^3} - {\left( 1 \right)^2} - 3\left( 1 \right) + 1 = 0 $ 

And  $ f\left( { - 1} \right) = 3{\left( { - 1} \right)^3} - {\left( { - 1} \right)^2} - 3\left( { - 1} \right) + 1 =  - 3 - 1 + 3 + 1 = 0 $ 

Hence,  $ \left( {x - 1} \right) $   $ \left( {x + 1} \right) $ ,  will be factors of  $ f\left( x \right) $ .

 $  \Rightarrow \left( {x - 1} \right)\left( {x + 2} \right) = {x^2} - 1 $  will be factor of  $ f\left( x \right) $ .

Let's now divide  $ f\left( x \right) = 3{x^3} - {x^2} - 3x + 1 $  by  $ {x^2} - 1 $  to get the other factors of  $ f\left( x \right) $ .

By long division, we have 

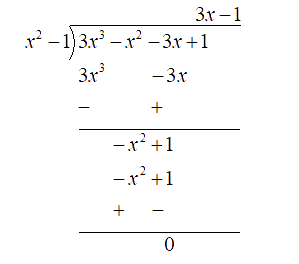
 $ 3{x^3} - {x^2} - 3x + 1 = \left( {{x^2} - 1} \right)\left( {3x - 1} \right) $ 

 $  \Rightarrow 3{x^3} - {x^2} - 3x + 1 = \left( {x - 1} \right)\left( {x + 1} \right)\left( {3x - 1} \right) $ 

Hence,  $ 3{x^3} - {x^2} - 3x + 1 = \left( {x - 1} \right)\left( {x + 1} \right)\left( {3x - 1} \right) $ 

25. Using suitable identify, evaluate the following:

(i)  $ {103^3} $ 

Ans: $ {103^3} = {\left( {100 + 3} \right)^3} $ 

Now using identify  $ {\left( {a + b} \right)^3} = {a^3} + {b^3} + 3ab\left( {a + b} \right) $ , we have

 $ {\left( {100 + 3} \right)^3} = {\left( {100} \right)^3} + {\left( 3 \right)^3} + 3\left( {100} \right)\left( 3 \right)\left( {100 + 3} \right) $ 

 $  = 1000000 + 27 + 900\left( {100 + 3} \right) $ 

 $  = 1000000 + 27 + 90000 + 2700 $ 

 $  = 1092727 $ 

(ii)  $ 101 \times 102 $ 

Ans: $ 101 \times 102 $ 

 $  = \left( {100 + 1} \right)\left( {100 + 2} \right) $  (using  $ \left( {x + a} \right)\left( {x + b} \right) = {x^2} + \left( {a + b} \right)x + ab $ )

We have,

 $  = {\left( {100} \right)^2} + \left( {1 + 2} \right)100 + \left( 1 \right)\left( 2 \right) $ 

 $  = 10000 + \left( 3 \right)100 + 2 = 10000 + 300 + 2 = 10302 $ 

(iii)  $ {999^2} $ 

Ans: $ {999^2} $ 

Ans:  $ {\left( {1000 - 1} \right)^2} $ 

 $  = {\left( {1000} \right)^2} - 2\left( {1000} \right) \times 1 + {1^2} $ 

 $  = 1000000 - 2000 + 1 = 998001 $ 

26. Factorise the following:

(i)  $ 4{x^2} + 20x + 25 $ 

Ans: We have,

 $ 4{x^2} + 20x + 25 = {\left( {2x} \right)^2} + 2\left( {2x} \right)5 + {\left( 5 \right)^2} $ 

 $  = {\left( {2x + 5} \right)^2} $   $ \left[ {{a^2} + 2ab + {b^2} = {{\left( {a + b} \right)}^2}} \right] $ 

 $  = \left( {2x + 5} \right)\left( {2x + 5} \right) $ 

(ii)  $ 9{y^2} - 66yz + 121{z^2} $ 

Ans: We have,

 $ 9{y^2} - 66yz + 121{z^2} = {\left( {3y} \right)^2} - 2\left( {3y} \right)\left( {11z} \right) + {\left( { - 11z} \right)^2} $ 

 $  = {\left( {3y - 11z} \right)^2} $   $ \left[ {{a^2} + {b^2} - 2ab = {{\left( {a - b} \right)}^2}} \right] $ 

 $  = \left( {3y - 11} \right)\left( {3y - 11} \right) $ 

(iii)  $ {\left( {2x + \dfrac{1}{3}} \right)^2} - {\left( {x - \dfrac{1}{2}} \right)^2} $ 

Ans: $ {\left( {2x + \dfrac{1}{3}} \right)^2} - {\left( {x - \dfrac{1}{2}} \right)^2} $ 

Now, using identity  $ {a^2} - {b^2} = \left( {a + b} \right)\left( {a - b} \right) $ 

 $  = \left[ {\left( {2x + \dfrac{1}{3}} \right) + \left( {x - \dfrac{1}{2}} \right)} \right]\left[ {\left( {2x + \dfrac{1}{3}} \right) - \left( {x - \dfrac{1}{2}} \right)} \right] $ 

 $  = \left( {2x + \dfrac{1}{3} + x - \dfrac{1}{2}} \right)\left( {2x + \dfrac{1}{3} - x + \dfrac{1}{2}} \right) = \left( {3x - \dfrac{1}{6}} \right)\left( {x + \dfrac{5}{6}} \right) $ 

27. Factorise the following:

(i)  $ 9{x^2} - 12x + 3 $ 

Ans: we have,

 $ 9{x^2} - 12x + 3 = 9{x^2} - 9x - 3x + 3 $ 

 $  = 9x\left( {x - 1} \right) - 3\left( {x - 1} \right) $ 

 $  = \left( {9x - 3} \right)\left( {x - 1} \right) $ 

 $  = 3\left( {3x - 1} \right)\left( {x - 1} \right) $ 

(ii)  $ 9{x^2} - 12x + 4 $ 

Ans: We have,

 $ 9{x^2} - 12x + 4 = {\left( {3x} \right)^2} - 2\left( {3x} \right)\left( 2 \right) + {\left( 2 \right)^2} $ 

 $  = {\left( {3x - 2} \right)^2}\left[ {{a^2} - 2ab + {b^2} = {{\left( {a - b} \right)}^2}} \right] $ 

 $  = \left( {3x - 2} \right)\left( {3x - 2} \right) $ 

28. Expand the following:

(i)  $ {\left( {4a - b + 2c} \right)^2} $ 

Ans: We have,

 $ {\left( {4a - b + 2c} \right)^2} = {\left( {4a} \right)^2} + {\left( { - b} \right)^2} + {\left( {2c} \right)^2} + 2\left( {4a} \right)\left( { - b} \right) + 2\left( { - b} \right)\left( {2c} \right) + 2\left( {2c} \right)\left( {4a} \right) $ 

Using  $ \left[ {{a^2} + b + {c^2} + 2ab + 2bc + 2ca = {{\left( {a + b + c} \right)}^2}} \right] $ 

 $  = 16{a^2} + {b^2} + 4{c^2} - 8ab - 4bc + 16ca $ 

(ii)  $ {\left( {3a - 5b - c} \right)^2} $ 

Ans: We have,

 $ {\left( {3a - 5b - c} \right)^2} = {\left( {3a} \right)^2} + {\left( { - 5b} \right)^2} + {\left( { - c} \right)^2} + 2\left( {3a} \right)\left( { - 5b} \right) + 2\left( { - 5b} \right)\left( { - c} \right) + 2\left( { - c} \right)\left( {3a} \right) $ 

Using  $ \left[ {{a^2} + {b^2} + {c^2} + 2ab + 2bc + 2ca = {{\left( {a + b + c} \right)}^2}} \right] $ 

 $  = 9{a^2} + 25{b^2} + {c^2} - 30ab + 10bc - 6ca $ 

(iii)  $ {\left( { - x + 2y - 3z} \right)^2} $ 

Ans: We have

 $ {\left( { - x + 2y - 3z} \right)^2} = {\left( { - x} \right)^2} + {\left( {2y} \right)^2} + {\left( { - 3z} \right)^2} + 2\left( { - x} \right)\left( {2y} \right) + 2\left( {2y} \right)\left( { - 3z} \right) + 2\left( { - 3z} \right)\left( { - x} \right) $ 

 $  = {x^2} + 4{y^2} + 9{z^2} - 4xy - 12yz + 6xz $ 

29. Factorise the following:

(i)  $ 9{x^2} + 4{y^2} + 16{z^2} + 12xy - 16yz - 24xz $ 

Ans: We have,

 $  \Rightarrow {\left( {3x} \right)^2} + {\left( {2y} \right)^2} + {\left( { - 4z} \right)^2} + 2\left( {3x} \right)\left( {2y} \right) + 2\left( {2y} \right)\left( { - 4z} \right) + 2\left( { - 4z} \right)\left( {3x} \right) $ 

 $  \Rightarrow {\left\{ {3x + 2y + \left( { - 4z} \right)} \right\}^2}\,\left[ {{a^2} + {b^2} + {c^2} + 2ab + 2bc + 2ca = {{\left( {a + b + c} \right)}^2}} \right] $ 

 $  \Rightarrow {\left( {3x + 2y - 4z} \right)^2} = \left( {3x + 2y - 4z} \right)\left( {3x + 2y - 4z} \right) $ 

(ii)  $ 25{x^2} + 16{y^2} + 4{z^2} - 40xy + 16yz - 20xz $ 

Ans: We have,

 $  \Rightarrow {\left( { - 5x} \right)^2} + {\left( {4y} \right)^2} + {\left( {2z} \right)^2} + 2\left( { - 5x} \right)\left( {4y} \right) + 2\left( {4y} \right)\left( {2z} \right) + 2\left( {2z} \right)\left( { - 5x} \right) $ 

 $  \Rightarrow {\left\{ { - 5x + 4y + 2z} \right\}^2}\,\left[ {{a^2} + {b^2} + {c^2} + 2ab + 2bc + 2ca = {{\left( {a + b + c} \right)}^2}} \right] $ 

(iii)  $ 16{x^2} + 4{y^2} + 9{z^2} - 16xy - 12yz + 24xz $ 

Ans: We have,

 $  \Rightarrow {\left( {4x} \right)^2} + {\left( { - 2y} \right)^2} + {\left( {3z} \right)^2} + 2\left( {4x} \right)\left( { - 2y} \right) + 2\left( { - 2y} \right)\left( {3z} \right) + 2\left( {3z} \right)\left( {4x} \right) $ 

 $  \Rightarrow {\left\{ {4x - 2y + 3z} \right\}^2}\,\left[ {{a^2} + {b^2} + {c^2} + 2ab + 2bc + 2ca = {{\left( {a + b + c} \right)}^2}} \right] $ 

 $  \Rightarrow {\left( {4x - 2y + 3z} \right)^2} = \left( {4x - 2y + 3z} \right)\left( {4x - 2y + 3z} \right) $ 

30. If  $ a + b + c = 9 $  and  $ ab + bc + ca = 26 $ , find  $ {a^2} + {b^2} + {c^2} $ .

Ans: We know that 

 $ {\left( {a + b + c} \right)^2} = {a^2} + {b^2} + {c^2} + 2ab + 2bc + 2ca $ 

 $  \Rightarrow {\left( {a + b + c} \right)^2} = \left( {{a^2} + {b^2} + {c^2}} \right) + 2\left( {ab + bc + ca} \right) $ 

Now, on putting the values, we get

 $  \Rightarrow {\left( 9 \right)^2} = \left( {{a^2} + {b^2} + {c^2}} \right) + 2\left( {26} \right) $ 

 $  \Rightarrow {a^2} + {b^2} + {c^2} = 81 - 52 = 29 $ 

31. Expand the following:

(i)  $ {\left( {3a - 2b} \right)^3} $ 

Ans: We have

 $ {\left( {3a - 2b} \right)^3} = {\left( {3a} \right)^3} - {\left( {2b} \right)^3} - 3\left( {3a} \right)\left( {2b} \right)\left( {3a - 2b} \right) $ 

Now, using identity  $ \left[ {{{\left( {a - b} \right)}^3} = {a^3} - {b^3} - 3ab\left( {a - b} \right)} \right] $ 

 $  = 27{a^3} - 8{b^3} - 54{a^2}b + 36a{b^2} $ 

(ii)  $ {\left( {\dfrac{1}{x} + \dfrac{y}{3}} \right)^3} $ 

Ans: Here, using the identity  $ \left[ {{{\left( {a + b} \right)}^3} = {a^3} + {b^3} + 3ab\left( {a + b} \right)} \right] $ 

 $ {\left( {\dfrac{1}{x} + \dfrac{y}{3}} \right)^3} = {\left( {\dfrac{1}{x}} \right)^3} + {\left( {\dfrac{y}{3}} \right)^3} + 3 \times \dfrac{1}{x} \times \dfrac{y}{3}\left( {\dfrac{1}{x} + \dfrac{y}{3}} \right) $ 

 $  \Rightarrow \dfrac{1}{{{x^3}}} + \dfrac{{{y^3}}}{{27}} + \dfrac{y}{x}\left( {\dfrac{1}{x} + \dfrac{y}{3}} \right) $ 

 $  \Rightarrow \dfrac{1}{{{x^3}}} + \dfrac{{{y^3}}}{{27}} + \dfrac{y}{{{x^2}}} + \dfrac{{{y^2}}}{{3x}} $ 

(iii)  $ {\left( {4 - \dfrac{1}{{3x}}} \right)^3} $ 

Ans: We have

 $ {\left( {4 - \dfrac{1}{{3x}}} \right)^3} = {\left( 4 \right)^3} - {\left( {\dfrac{1}{{3x}}} \right)^3} - 3\left( 4 \right)\left( {\dfrac{1}{{3x}}} \right)\left( {4 - \dfrac{1}{{3x}}} \right) $ 

Now, using identity  $ \left[ {{{\left( {a - b} \right)}^3} = {a^3} - {b^3} - 3ab\left( {a - b} \right)} \right] $ 

 $  = 64 - \dfrac{1}{{27{x^3}}} - \dfrac{4}{x}\left( {4 - \dfrac{1}{{3x}}} \right) $ 

 $  = 64 - \dfrac{1}{{27{x^3}}} - \dfrac{{16}}{x} + \dfrac{4}{{3{x^2}}} $ 

32.Factorise the following:

(i)  $ 1 - 64{a^3} - 12a + 48{a^2} $ 

Ans: We have,

 $ 1 - 64{a^3} - 12a + 48{a^2} = {\left( 1 \right)^3} - {\left( {4a} \right)^3} - 3\left( 1 \right)\left( {4a} \right)\left( {1 - 4a} \right) $ 

 $  = {\left( {1 - 4a} \right)^3}\left[ {{a^3} - {b^3} - 3ab\left( {a - b} \right) = {{\left( {a - b} \right)}^3}} \right] $ 

 $  = \left( {1 - 4a} \right)\left( {1 - 4a} \right)\left( {1 - 4a} \right) $ 

(ii)  $ 8{p^3} + \dfrac{{12}}{5}{p^2} + \dfrac{6}{{25}}p + \dfrac{1}{{125}} $ 

Ans: We have,

$ 8{p^3} + \dfrac{{12}}{5}{p^2} + \dfrac{6}{{25}}p + \dfrac{1}{{125}} $ 

 $  = {\left( {2p} \right)^3} + 3 \times {\left( {2p} \right)^2} \times \dfrac{1}{5} + 3 \times \left( {2p} \right) \times {\left( {\dfrac{1}{5}} \right)^2} + {\left( {\dfrac{1}{5}} \right)^3} $ 

 $  = {\left( {2p} \right)^3} + {\left( {\dfrac{1}{5}} \right)^3} + 3 \times \left( {2p} \right) \times \dfrac{1}{5}\left[ {2p + \dfrac{1}{5}} \right] $ 

 $  = {\left( {2p + \dfrac{1}{5}} \right)^3} = \left( {2p + \dfrac{1}{5}} \right)\left( {2p + \dfrac{1}{5}} \right)\left( {2p + \dfrac{1}{5}} \right) $ 

33. Find the following products:

(i)  $ \left( {\dfrac{x}{2} + 2y} \right)\left( {\dfrac{{{x^2}}}{4} - xy + 4{y^2}} \right) $ 

Ans: We have,

 $ \left( {\dfrac{x}{2} + 2y} \right)\left( {\dfrac{{{x^2}}}{4} - xy + 4{y^2}} \right) = \left( {\dfrac{x}{y} + 2y} \right)\left( {{{\left( {\dfrac{x}{2}} \right)}^2} - \left( {\dfrac{x}{2}} \right)\left( {2y} \right) + {{\left( {2y} \right)}^2}} \right) $ 

 $  = {\left( {\dfrac{x}{2}} \right)^3} + {\left( {2y} \right)^3}\left[ {\left( {a + b} \right)\left( {{a^2} - ab + {b^2}} \right) = {a^3} + {b^3}} \right] $ 

 $  = \dfrac{{{x^3}}}{8} + 8{y^3} $ 

(ii)  $ \left( {{x^2} - 1} \right)\left( {{x^4} + {x^2} + 1} \right) $ 

Ans: We have,

 $ \left( {{{\left( x \right)}^2} - 1} \right)\left( {{x^4} + {x^2} + 1} \right) = \left( {{x^2} - 1} \right)\left( {{{\left( {{x^2}} \right)}^2} + \left( {{x^2}} \right)\left( 1 \right) + {{\left( 1 \right)}^2}} \right) $ 

 $  = {\left( {{x^2}} \right)^3} - {\left( 1 \right)^3}\left[ {\left( {a - b} \right)\left( {{a^2} + ab + {b^2}} \right) = {a^3} - {b^3}} \right] $ 

 $  = {x^6} - 1 $ 

34. Factorise:

(i)  $ 1 + 64{x^3} $ 

Ans: We have,

 $ 1 + 64{x^3} = {\left( 1 \right)^3} + {\left( {4x} \right)^3} $ 

 $  = \left( {1 + 4x} \right)\left( {{{\left( 1 \right)}^2} - \left( 1 \right)\left( {4x} \right) + {{\left( {4x} \right)}^2}} \right) $ 

 $  = \left( {1 + 4x} \right)\left( {1 - 4x + 16{x^2}} \right) $ 

(ii)  $ {a^3} - 2\sqrt {2{b^3}}  $ 

Ans: We have,

 $ {a^3} - 2\sqrt {2{b^3}}  = {\left( a \right)^3} - {\left( {\sqrt 2 b} \right)^3} $ 

 $  = \left( {a - \sqrt 2 b} \right)\left( {{{\left( a \right)}^2} + \left( a \right)\left( {\sqrt 2 b} \right) + {{\left( {\sqrt 2 b} \right)}^2}} \right) $ 

 $  = \left( {a - \sqrt 2 b} \right)\left( {{a^2} + \sqrt 2 ab + 2{b^2}} \right) $ 

35. Find the following product:

 $ \left( {2x - y + 3z} \right)\left( {4{x^2} + {y^2} + 9{z^2} + 2xy + 3yz - 6xz} \right) $ 

Ans: We have,

 $ \left( {2x - y + 3z} \right)\left( {4{x^2} + {y^2} + 9{z^2} + 2xy + 3yz - 6xz} \right) $ 

 $  = \left\{ {2x + \left( { - y} \right) + 3z} \right\}\left\{ {{{\left( {2x} \right)}^2} + {{\left( { - y} \right)}^2} + {{\left( {3z} \right)}^2} - 2x\left( { - y} \right) - \left( { - y} \right)\left( {3z} \right) - \left( { - y} \right)\left( {3z} \right) - \left( {3z} \right)\left( {2x} \right)} \right\} $ 

 $  = {\left( {2x} \right)^3} + {\left( { - y} \right)^3} + {\left( {3z} \right)^3} - 3\left( {2x} \right)\left( { - y} \right)\left( {3z} \right) $  

using identity  $ \left[ {\left( {a + b + c} \right)\left( {{a^2} + {b^2} + {c^2} - ab - bc - ca} \right) = {a^3} + {b^3} + {c^3} - 3abc} \right] $ 

 $  = 8{x^3} - {y^3} + 27{z^2} + 18xyz $ 

36.Factorise:

(i)  $ {a^3} - 8{b^3} - 64{c^3} - 24abc $ 

Ans: We have,

 $ {a^3} - 8{b^3} - 64{c^3} - 24abc $ 

 $  = \left\{ {{{\left( a \right)}^3} + {{\left( { - 2b} \right)}^3} + {{\left( { - 4c} \right)}^3} - 3\left( a \right)\left( { - 2b} \right)\left( { - 4c} \right)} \right\} $ 

 $  = \left\{ {a + \left( { - 2b} \right) + \left( { - 4c} \right)} \right\}\left\{ {{a^2} + {{\left( { - 2b} \right)}^2} + {{\left( { - 4c} \right)}^2} - a\left( { - 2b} \right) - \left( { - 2b} \right)\left( { - 4c} \right) - \left( { - 4c} \right)a} \right\} $ 

Using identity  $ \left[ {\left( {a + b + c} \right)\left( {{a^2} + {b^2} + {c^2} - ab - bc - ca} \right) = {a^3} + {b^3} + {c^3} - 3abc} \right] $ 

 $  = \left( {a - 2b - 4c} \right)\left( {{a^2} + 4{b^2} + 16{c^2} + 2ab - 8bc + 4ca} \right) $ 

(ii)  $ 2\sqrt 2 {a^3} + 8{b^3} - 27{c^3} + 18\sqrt 2 abc $ 

Ans: We have,

 $ 2\sqrt 2 {a^3} + 8{b^3} - 27{c^3} + 18\sqrt 2 abc $ 

 $  = \left\{ {{{\left( {\sqrt 2 a} \right)}^3} + {{\left( {2b} \right)}^3} + {{\left( { - 3c} \right)}^3} - 3\left( {\sqrt 2 a} \right)\left( {2b} \right)\left( { - 3c} \right)} \right\} $ 

 $  = \left\{ {\sqrt 2 a + 2b + \left( { - 3c} \right)} \right\}\left\{ {{{\left( {\sqrt 2 a} \right)}^2} + {{\left( {2b} \right)}^2} + {{\left( { - 3c} \right)}^2} - \left( {\sqrt 2 a} \right)\left( {2b} \right) - \left( {2b} \right)\left( { - 3c} \right) - \left( { - 3c} \right)\left( {\sqrt 2 a} \right)} \right\} $ 

Using identity  $ \left[ {\left( {a + b + c} \right)\left( {{a^2} + {b^2} + {c^2} - ab - bc - ca} \right) = {a^3} + {b^3} + {c^3} - 3abc} \right] $ 

 $  = \left( {\sqrt 2 a + 2b - 3c} \right)\left( {2{a^2} + 4{b^2} + 9{c^2} - 2\sqrt 2 ab + 6bc + 3\sqrt 2 ca} \right) $ 

37. Without actually calculating the cubes, find the value of:

(i)  $ {\left( {\dfrac{1}{2}} \right)^3} + {\left( {\dfrac{1}{3}} \right)^3} - {\left( {\dfrac{5}{6}} \right)^3} $ 

Ans:  Let  $ a = \dfrac{1}{2}\,,\,b = \dfrac{1}{3}\,,\,c =  - \dfrac{5}{6} $ 

 $ a + b + c = \dfrac{1}{2} + \dfrac{1}{3} - \dfrac{5}{6} $ 

 $  = \dfrac{{3 + 2 - 5}}{6} = \dfrac{0}{6} = 0 $ 

 $ \left[ {\left( {a + b + c} \right)\left( {{a^2} + {b^2} + {c^2} - ab - bc - ca} \right) = {a^3} + {b^3} + {c^3} - 3abc} \right] $ 

Therefore, 

 $  \Rightarrow {a^3} + {b^3} + {c^3} = 3abc $ 

 $  \Rightarrow 3 \times \dfrac{1}{2} \times \dfrac{1}{3} \times  - \dfrac{5}{6} $ 

 $  \Rightarrow  - \dfrac{5}{{12}} $ 

(ii)  $ {\left( {0.2} \right)^3} - {\left( {0.3} \right)^3} + {\left( {0.1} \right)^3} $ 

Ans: We have,

 $ {\left( {0.2} \right)^3} - {\left( {0.3} \right)^3} + {\left( {0.1} \right)^3} = {\left( {0.2} \right)^3} + {\left( { - 0.3} \right)^3} + {\left( {0.1} \right)^3} $ 

 $ a = 0.2\,,\,b =  - 0.3\,,\,c = 0.1 $ . Then,

 $ a + b + c = 0.2 - 0.3 - 0.1 = 0 $ .

 $ \left[ {\left( {a + b + c} \right)\left( {{a^2} + {b^2} + {c^2} - ab - bc - ca} \right) = {a^3} + {b^3} + {c^3} - 3abc} \right] $ 

Therefore, 

 $  \Rightarrow {a^3} + {b^3} + {c^3} = 3abc $ 

 $  \Rightarrow 3 \times 0.2 \times \left( { - 0.3} \right) \times \left( {0.1} \right) $ 

 $  \Rightarrow  - 0.018 $ 

Hence,  $ {\left( {0.2} \right)^3} - {\left( {0.3} \right)^3} + {\left( {0.1} \right)^3} =  - 0.018 $ 

38. Without finding the cubes, factorise

 $ {\left( {x - 2y} \right)^3} + {\left( {2y - 3z} \right)^3} + {\left( {3z - x} \right)^3} $ 

Ans: We have,

 $ {\left( {x - 2y} \right)^3} + {\left( {2y - 3z} \right)^3} + {\left( {3z - x} \right)^3} $ 

 $ a = x - 2y\,,\,b = 2y - 3z\,,\,c = 3z - x $ . Then,

 $ a + b + c = x - 2y + 2y - 3z + 3z - x = 0 $ .

 $ \left[ {\left( {a + b + c} \right)\left( {{a^2} + {b^2} + {c^2} - ab - bc - ca} \right) = {a^3} + {b^3} + {c^3} - 3abc} \right] $ 

Therefore, 

 $  \Rightarrow {a^3} + {b^3} + {c^3} = 3abc $ 

 $  \Rightarrow 3 \times \left( {x - 2y} \right) \times \left( {2y - 3z} \right) \times \left( {3z - x} \right) $ 

 $  \Rightarrow 3\left( {x - 2y} \right)\left( {2y - 3z} \right)\left( {3z - x} \right) $ 

39. Find the value of

(i)  $ {x^3} + {y^3} - 12xy + 64 $ , when  $ x + y =  - 4 $ 

Ans: $ {x^3} + {y^3} - 12xy + 64 = {x^3} + {y^3} + {4^3} - 3xy\left( 4 \right) $ 

 $  = \left( {x + y + 4} \right)\left( {{x^2} + {y^2} + {4^2} - xy - 4y - 4x} \right) $ 

 $ \left[ {x + y =  - 4} \right] $ 

 $  = \left( 0 \right)\left( {{x^2} + {y^2} + {4^2} - xy - 4y - 4x} \right) = 0 $ 

(ii)  $ {x^3} - 8{y^3} - 36xy - 216 $ , when  $ x = 2y + 6 $ 

Ans: $ {x^3} - 8{y^3} - 36xy - 216 = {x^3} + {\left( { - 2y} \right)^3} + {\left( { - 6} \right)^3} - 3x\left( { - 2y} \right)\left( { - 6} \right) $ 

 $  = \left( {x - 2y - 6} \right)\left( {{x^2} + {{\left( { - 2y} \right)}^2} + {{\left( { - 6} \right)}^2} - x\left( { - 2y} \right) - \left( { - 2y} \right)\left( { - 6} \right) - x\left( { - 6} \right)} \right) $ 

 $  = \left( {x - \left( {2y + 6} \right)} \right)\left( {{x^2} + {{\left( { - 2y} \right)}^2} + {{\left( { - 6} \right)}^2} - x\left( { - 2y} \right) - \left( { - 2y} \right)\left( { - 6} \right) - x\left( { - 6} \right)} \right) $ 

 $ \left[ {x = 2y + 6} \right] $ 

 $  = \left( 0 \right)\left( {{x^2} + 4{y^2} + 36 + 2xy - 12y + 6x} \right) = 0 $ 

40. Give possible experiments for the length and breadth of the rectangle whose area is given by  $ 4{a^2} + 4a - 3 $ 

Ans: Area  $ 4{a^2} + 4a - 3 $ .

Here we will use a method of splitting the middle term.

Here we have to split the middle term as  $ 4a = 6a - 2a $ 

Now,

  $  \Rightarrow 4{a^2} + \left( {6a - 2a} \right) - 3 $ 

 $  \Rightarrow 4{a^2} + 6a - 2a - 3 $ 

 $  \Rightarrow 2a\left( {2a + 3} \right) - 1\left( {2a + 3} \right) $ 

 $  \Rightarrow \left( {2a - 1} \right)\left( {2a + 3} \right) $ 

We know that, area of rectangle \[ = 4{a^2} + 4a - 3\]

Here we also know that, area of a rectangle  $  = \,length\, \times \,breadth $  and  $ 4{a^2} + 4a - 3 = \left( {2a - 1} \right)\left( {2a + 3} \right) $ .

Therefore, its possible length and breadth  $  = \,\left( {2a - 1} \right) $  and   $ \left( {2a + 3} \right) $  or, we can say that  $ length = \left( {2a + 3} \right) $  and  $ breadth\, = \,\left( {2a - 1} \right) $ .

Long Answer Questions

Sample Question 1.  If \[x{\text{ }} + {\text{ }}y{\text{ }} = {\text{ }}12\] and \[xy{\text{ }} = {\text{ }}27\], find the value of \[{x^3}{\text{ }} + {\text{ }}{y^3}\].

Ans: Here we will use an identity, \[{\text{ }}{\left( {x{\text{ }} + {\text{ }}y} \right)^3}{\text{ =  }}{x^3}{\text{ }} + {\text{ }}{y^3}{\text{  +  }}3xy{\text{ }}\left( {x{\text{ }} + {\text{ }}y} \right)\]

\[{x^3}{\text{ }} + {\text{ }}{y^3}{\text{ }} = {\text{ }}{\left( {x{\text{ }} + {\text{ }}y} \right)^3}{\text{ }}-{\text{ }}3xy{\text{ }}\left( {x{\text{ }} + {\text{ }}y} \right)\] 

\[{\text{ =  }}{12^3}{\text{ }}-{\text{ }}3{\text{ }} \times {\text{ }}27{\text{ }} \times {\text{ }}12\]

\[ = {\text{ }}12{\text{ }}\left[ {{{12}^2}{\text{ }}-{\text{ }}3{\text{ }} \times {\text{ }}27} \right]\]

\[ = {\text{ }}12{\text{ }} \times {\text{ }}63\]

\[ = {\text{ }}756\]

Therefore, the value of \[{x^3}{\text{ }} + {\text{ }}{y^3} = 756\].

EXERCISE 2.4   

1. If the Polynomials  $ a{z^3} + 4{z^2} + 3z - 4 $  and  $ {z^3} - 4z + a $  leave the same remainder when divided  $ z - 3 $ , by Find the value of a.

Ans: We have,

 $ p\left( z \right) = a{z^3} + 4{z^2} + 3z - 4 $ 

And  $ q\left( z \right) = {z^3} - 4z + a $ 

As it is given that both the Polynomials leave the same remainder when divided by  $ z - 3 $ .

Therefore,

 $ p\left( 3 \right) = q\left( 3 \right) $ 

\[ \Rightarrow a{\left( 3 \right)^3} + 4{\left( 3 \right)^2} + 3\left( 3 \right) - 4 = \,{\left( 3 \right)^3} - 4\left( 3 \right) + a\]

\[ \Rightarrow 27a + 4 \times 9 + 9 - 4 = \,27 - 12 + a\]

\[ \Rightarrow 27a + 36 + 5 = \,15 + a\]

 $  \Rightarrow 27a - a = 15 - 41 $ 

 $  \Rightarrow 26a =  - 26 $ 

 $  \Rightarrow a =  - 1 $ 

Hence, the required value of a is  $  - 1 $ .

2. The Polynomial  $ p\left( x \right) = {x^4} - 2{x^3} + 3{x^2} - ax + 3a - 7 $ when divided by  $ x + 1 $  leave remainder  $ 19 $ . Also, find the remainder when  $ p\left( x \right) $  is divided by  $ x + 2 $ .

Ans: We know that when  $ p\left( x \right) $  is divided by  $ x + b $ , then the remainder  $  = \,p\left( { - b} \right) $ 

Now,  $ p\left( x \right) = {x^4} - 2{x^3} + 3{x^2} - ax + 3a - 7 $ is divided by  $ x + 1 $ , then the remainder  $  = \,p\left( { - 1} \right) $ .

Also, we know that the remainder is  $ 19 $ .

Therefore,

 $ \,p\left( { - 1} \right) = 19 $ 

 $ {\left( { - 1} \right)^4} - 2{\left( { - 1} \right)^3} + 3{\left( { - 1} \right)^2} - a\left( { - 1} \right) + 3a - 7 = 19 $ 

 $  \Rightarrow 1 + 2 + 3 + a + 3a - 7 = 19 $ 

 $  \Rightarrow 4a - 1 = 19 $ 

 $  \Rightarrow 4a = 20 $ 

 $  \Rightarrow a = 5 $ 

Now,  $ p\left( x \right) = {x^4} - 2{x^3} + 3{x^2} - 5x + 3\left( 5 \right) - 7 = {x^4} - 2{x^3} + 3{x^2} - 5x + 8 $ 

Again, when p(x) is divided by  $ x + 2 $ , then

Remainder  $  = p\left( { - 2} \right) = {\left( { - 2} \right)^4} - 2{\left( { - 2} \right)^3} + 3{\left( { - 2} \right)^2} - 5\left( { - 2} \right) + 8 $ 

 $  = 16 + 16 + 12 + 10 + 8 $ 

 $  = 62 $ 

3. If both \[\left( {x - 2} \right)\] and  $ \left( {x - \dfrac{1}{2}} \right) $  are factors of  $ p{x^2} + 5x + r $ , Show that  $ p = r $ .

Ans: Let  $ q\left( x \right) = p{x^2} + 5x + r $ 

As  $ \left( {x - 2} \right) $  is a factor of  $ q\left( x \right) $ 

Then,  $ q\left( 2 \right) = 0 $ 

 $  \Rightarrow p{\left( 2 \right)^2} + 5\left( 2 \right) + r = 0 $ 

 $  \Rightarrow 4p + 10 + r = 0 $ 

 $  \Rightarrow  - 4p - r = 10............\left( 1 \right) $ 

Again,  $ \left( {x - \dfrac{1}{2}} \right) $  is a factor of  $ q\left( x \right) $ .

Then,  $ q\left( {\dfrac{1}{2}} \right) = 0 $ 

 $  \Rightarrow p{\left( {\dfrac{1}{2}} \right)^2} + 5\left( {\dfrac{1}{2}} \right) + r = 0 $ 

 $  \Rightarrow \dfrac{p}{4} + \dfrac{5}{2} + r = 0 $ 

 $  \Rightarrow p + 10 + 4r = 0 $ 

Now, using equation  $ 1 $ 

 $  \Rightarrow p - 4p - r + 4r = 0 $ 

 $  \Rightarrow  - 3p + 3r = 0 $ 

 $  \Rightarrow p = r $ 

Hence, proved.

4. Without actual division, prove that  $ 2{x^4} - 5{x^3} + 2{x^2} - x + 2 $  is divisible by  $ {x^2} - 3x + 2 $ .

Ans: We have,

 $ {x^2} - 3x + 2 $ 

We can also write it as

 $  \Rightarrow {x^2} - 3x + 2 = {x^2} - 2x - x + 2 $ 

 $  \Rightarrow x\left( {x - 2} \right) - 1\left( {x - 2} \right) = \left( {x - 1} \right)\left( {x - 2} \right) $ 

Now, we have

 $ p\left( x \right) = 2{x^4} - 5{x^3} + 2{x^2} - x + 2 $ 

Put  $ x = 1 $ 

 $ p\left( 1 \right) = 2{\left( 1 \right)^4} - 5{\left( 1 \right)^3} + 2{\left( 1 \right)^2} - \left( 1 \right) + 2 $ 

 $ p\left( 1 \right) = 2 - 5 + 2 + 1 = 0 $ 

 $ p\left( 1 \right) = 0 $ 

Therefore,  $ x - 1 $  divides p(x).

Put  $ x = 2 $ 

 $ p\left( 2 \right) = 2{\left( 2 \right)^4} - 5{\left( 2 \right)^3} + 2{\left( 2 \right)^2} - \left( 2 \right) + 2 $ 

 $ p\left( 2 \right) = 32 - 40 + 8 - 2 + 2 = 0 $ 

 $ p\left( 2 \right) = 0 $ 

Therefore,  $ x - 2 $  divides p(x).

Hence, $ {x^2} - 3x + 2 $ divides $ 2{x^4} - 5{x^3} + 2{x^2} - x + 2 $ .

5. Simplify  $ {\left( {2x - 5y} \right)^3} - {\left( {2x + 5y} \right)^3} $ .

Ans: We have,

 $  = {\left( {2x - 5y} \right)^3} - {\left( {2x + 5y} \right)^3} $ 

Now, using  $ {a^3} - {b^3} = \left( {a - b} \right)\left( {{a^2} + ab + {b^2}} \right) $ 

 $  = \left\{ {\left( {2x - 5y} \right) - \left( {2x + 5y} \right)} \right\}\left\{ {{{\left( {2x - 5y} \right)}^2} + \left( {2x - 5y} \right)\left( {2x + 5y} \right) + {{\left( {2x + 5} \right)}^2}} \right\} $ 

 $  = \left( { - 10y} \right)\left( {2{x^2} + 25{y^2}} \right) $ 

 $  =  - 120{x^2}y - 250{y^3} $ 

6. Multiply  $ {x^2} + 4{y^2} + {z^2} + 2xy + xz - 2yz $  by  $ \left( { - z + x - 2y} \right) $ .

Ans: We have,

 $ \left( { - z + x - 2y} \right)\left( {{x^2} + 4{y^2} + {z^2} + 2xy + xz - 2yz} \right) $ 

 $  = \left\{ {x + \left( { - 2y} \right) + \left( { - z} \right)} \right\}\left\{ {{{\left( x \right)}^2} + {{\left( { - 2y} \right)}^2} + {{\left( { - z} \right)}^2} - \left( x \right)\left( { - 2y} \right) - \left( x \right)\left( { - z} \right) - \left( -2y \right)\left( { - z} \right)} \right\} $ 

 $  = {x^3} + {\left( { - 2y} \right)^3} + {\left( { - z} \right)^3} - 3\left( x \right)\left( { - 2y} \right)\left( { - z} \right) $ 

 $  = {x^3} - 8{y^3} - {z^3} - 6xyz $ 

7. If a, b, c are all non-zero and \[a + b + c = 0\], prove that  $ \dfrac{{{a^2}}}{{bc}} + \dfrac{{{b^2}}}{{ca}} + \dfrac{{{c^2}}}{{ab}} = 3 $ .

Ans: Here, a, b, c are all non-zero and \[a + b + c = 0\].

Therefore,

 $ {a^3} + {b^3} + {c^3} = 3abc $ 

Now, we will divide the complete equation by abc.

 $ \dfrac{{{a^3}}}{{abc}} + \dfrac{{{b^3}}}{{abc}} + \dfrac{{{c^3}}}{{abc}} = \dfrac{{3abc}}{{abc}} $ 

 $ \dfrac{{{a^2}}}{{bc}} + \dfrac{{{b^2}}}{{ca}} + \dfrac{{{c^2}}}{{ab}} = 3 $ .

8. If  $ a + b + c = 5 $  and  $ ab + bc + ca = 10 $ , then prove that  $ {a^3} + {b^3} + {c^3} - 3abc =  - 25 $ .

Ans: We know that, 

 $ {a^3} + {b^3} + {c^3} - 3abc = \left( {a + b + c} \right)\left( {{a^2} + {b^2} + {c^2} - ab - bc - ca} \right) $ 

 $  = \left( {a + b + c} \right)\left( {{a^2} + {b^2} + {c^2} - \left( {ab + bc + ca} \right)} \right) $ 

It is given that  $ a + b + c = 5 $  and  $ ab + bc + ca = 10 $ .

 $  = 5\left( {{a^2} + {b^2} + {c^2} - 10} \right) $ 

Now, we have 

 $ a + b + c = 5 $ 

Squaring both sides, we get

 $ {\left( {a + b + c} \right)^2} = {\left( 5 \right)^2} $ 

 $ {a^2} + {b^2} + {c^2} + 2\left( {ab + bc + ca} \right) = 25 $ 

 $ {a^2} + {b^2} + {c^2} + 2\left( {10} \right) = 25 $ 

 $ {a^2} + {b^2} + {c^2} = 25 - 20 = 5 $ 

Now, put the above value in equation  $  = 5\left( {{a^2} + {b^2} + {c^2} - 10} \right) $ 

 $  = 5\left( {5 - 10} \right) $ 

 $  = 5 \times  - 5 =  - 25 $ 

Hence, proved.

9. Prove that  $ {\left( {a + b + c} \right)^3} - {a^3} - {b^3} - {c^3} = 3\left( {a + b} \right)\left( {b + c} \right)\left( {c + a} \right) $ .

Ans:  $ {\left( {a + b + c} \right)^3} = {\left[ {a + \left( {b + c} \right)} \right]^3} $ 

 $  = {a^3} + 3{a^2}\left( {b + c} \right) + 3a{\left( {b + c} \right)^2} + {\left( {b + c} \right)^3} $ 

 $  = {a^3} + 3{a^2}b + 3{a^2}c + 3a\left( {{b^2} + 2bc + {c^2}} \right) + \left( {{b^3} + 3{b^2}c + 3b{c^2} + {c^3}} \right) $ 

 $  = {a^3} + 3{a^2}b + 3{a^2}c + 3a{b^2} + 6abc + 3a{c^2} + {b^3} + 3{b^2}c + 3b{c^2} + {c^3} $ 

 $  = {a^3} + {b^3} + {c^3} + 3{a^2}b + 3{a^2}c + 3a{b^2} + 6abc + 3a{c^2} + 3{b^2}c + 3b{c^2} $ 

We can also write it as,

 $  = {a^3} + {b^3} + {c^3} + 3abc + 3{a^2}b + 3a{c^2} + 3{a^2}c + 3{b^2}c + 3{b^2}a + 3b{c^2} + 3abc $ 

 $  = {a^3} + {b^3} + {c^3} + 3ab\left( {a + c} \right) + 3ac\left( {a + c} \right) + 3{b^2}\left( {a + c} \right) + 3bc\left( {a + c} \right) $ 

 $  = {a^3} + {b^3} + {c^3} + \left( {a + c} \right)\left( {3ab + 3ac + 3{b^2} + 3bc} \right) $ 

 $  = {a^3} + {b^3} + {c^3} + \left( {a + c} \right)\left( {3a\left( {b + c} \right) + 3b\left( {b + c} \right)} \right) $ 

 $  = {a^3} + {b^3} + {c^3} + \left( {a + c} \right)\left( {b + c} \right)\left( {3a + 3b} \right) $ 

 $  = {a^3} + {b^3} + {c^3} + 3\left( {a + c} \right)\left( {b + c} \right)\left( {a + b} \right) $ 

Now, on transposing we get

 $ {\left( {a + b + c} \right)^3} - {a^3} - {b^3} - {c^3} = 3\left( {a + b} \right)\left( {b + c} \right)\left( {c + a} \right) $ 

Hence, proved.

Introduction to NCERT Exemplar

NCERT Exemplar Class 9 Maths Solutions Chapter 2 'Polynomials' will give you data in regards to polynomials and their applications. The part of NCERT Exemplar Class 9 Maths incorporates various topics like entire numbers, integers, rational numbers, kinds of polynomials, zeros of polynomials, and so forth This part contains 4 activities and the evaluations of the around 60 model problems.

Polynomials of Class 9 NCERT comprise of very clear cut theory for students to do more practice that needs to solve questions given in the model. Chapter 2 comprises issues dependent on Factorization of Polynomials and Algebraic Identities and polynomials in one variable, Zeros of a Polynomial. Another significant formula you will comprehend is Remainder Theorem.

Importance of NCERT Class 9 Maths Exemplar Book

The NCERT Class 9 Maths Exemplar book comprises the important questions according to the assessment perspective. These NCERT Exemplar questions and answers for CBSE Class 9 Maths Chapter 2 are planned by the experts of maths who target at keeping each idea of the chapter clear for you. The experts at Vedantu have given you stepwise NCERT Exemplar arrangements so you can comprehend the ideas and score more marks in your CBSE tests.