NCERT Exemplar for Class 7 Maths Solutions Chapter 9 Perimeter & Area

Solved Examples

In Examples 1 and 2, there are four options, out of which one is correct. Choose the correct one.

1. Following rectangle is composed of \[{\mathbf{8}}\] congruent parts.

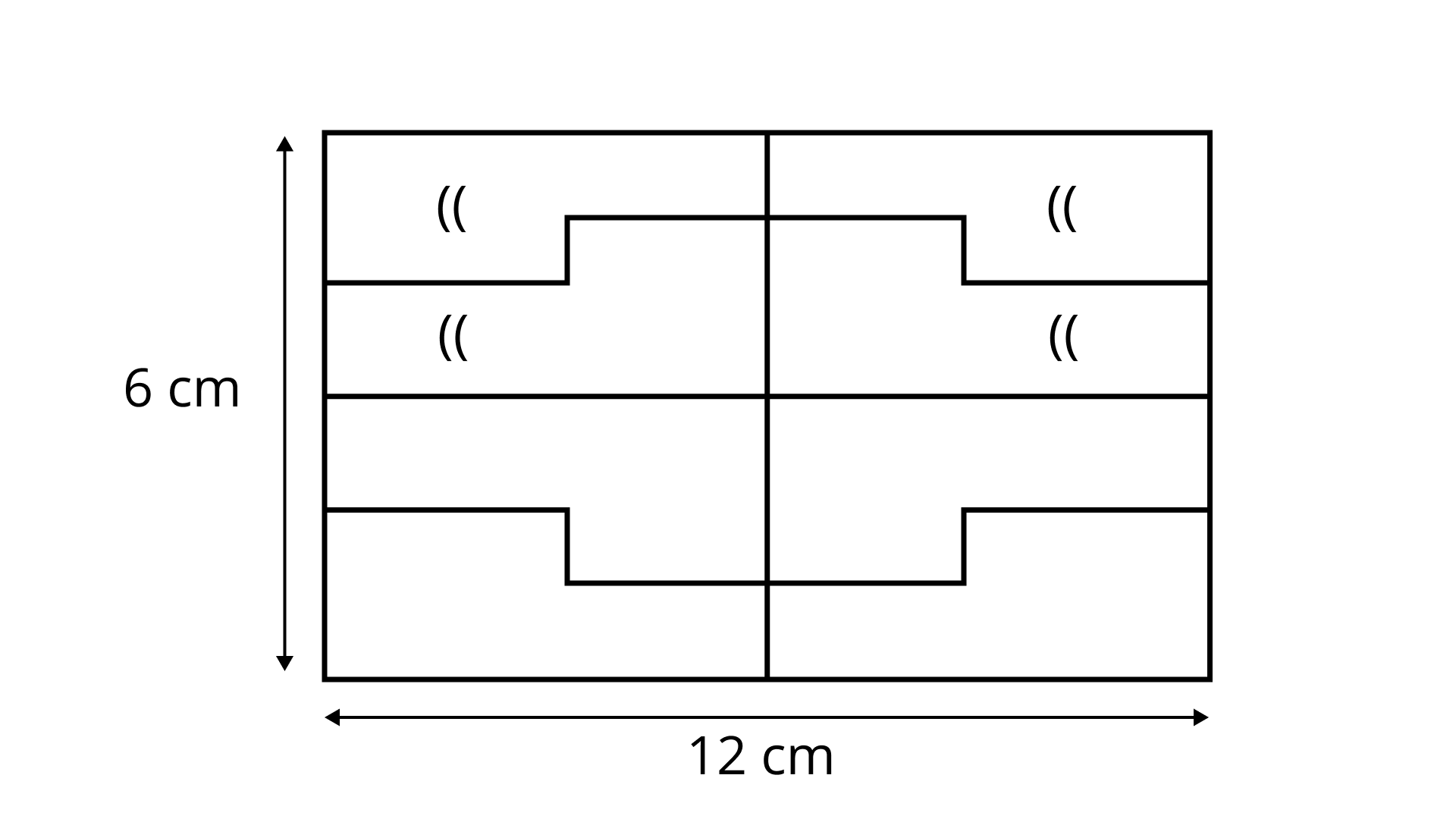
Area of each part is

(a) ${\mathbf{72\;c}}{{\mathbf{m}}^{\mathbf{2}}}$

(b) ${\mathbf{36\;c}}{{\mathbf{m}}^{\mathbf{2}}}$

(c) ${\mathbf{18\;c}}{{\mathbf{m}}^{\mathbf{2}}}$

(d) ${\mathbf{9\;c}}{{\mathbf{m}}^{\mathbf{2}}}$

Ans: Correct answer is (d).

Area of rectangle $ = $ length $ \times $ breadth

$ = 12\;{\text{cm}} \times 6\;{\text{cm}} = 72\;{\text{c}}{{\text{m}}^2}$

Since, rectangle is equivalent to 8 congruent

part,

As, we know congruent figures have equal areas

So, area of rectangle \[ = \]$8$(area of one of the 8 congruent parts)

So, area of one congruent part is $ = $$\dfrac{{{\text{ area of rectangle }}}}{8}$

$ = \dfrac{{72\;{\text{c}}{{\text{m}}^2}}}{8}$

$ = 9\;{\text{c}}{{\text{m}}^2}$

2. Area of a right triangle is ${\mathbf{54\;c}}{{\mathbf{m}}^{\mathbf{2}}}$. If one of its legs is ${\mathbf{12\;cm}}$ long, its perimeter is

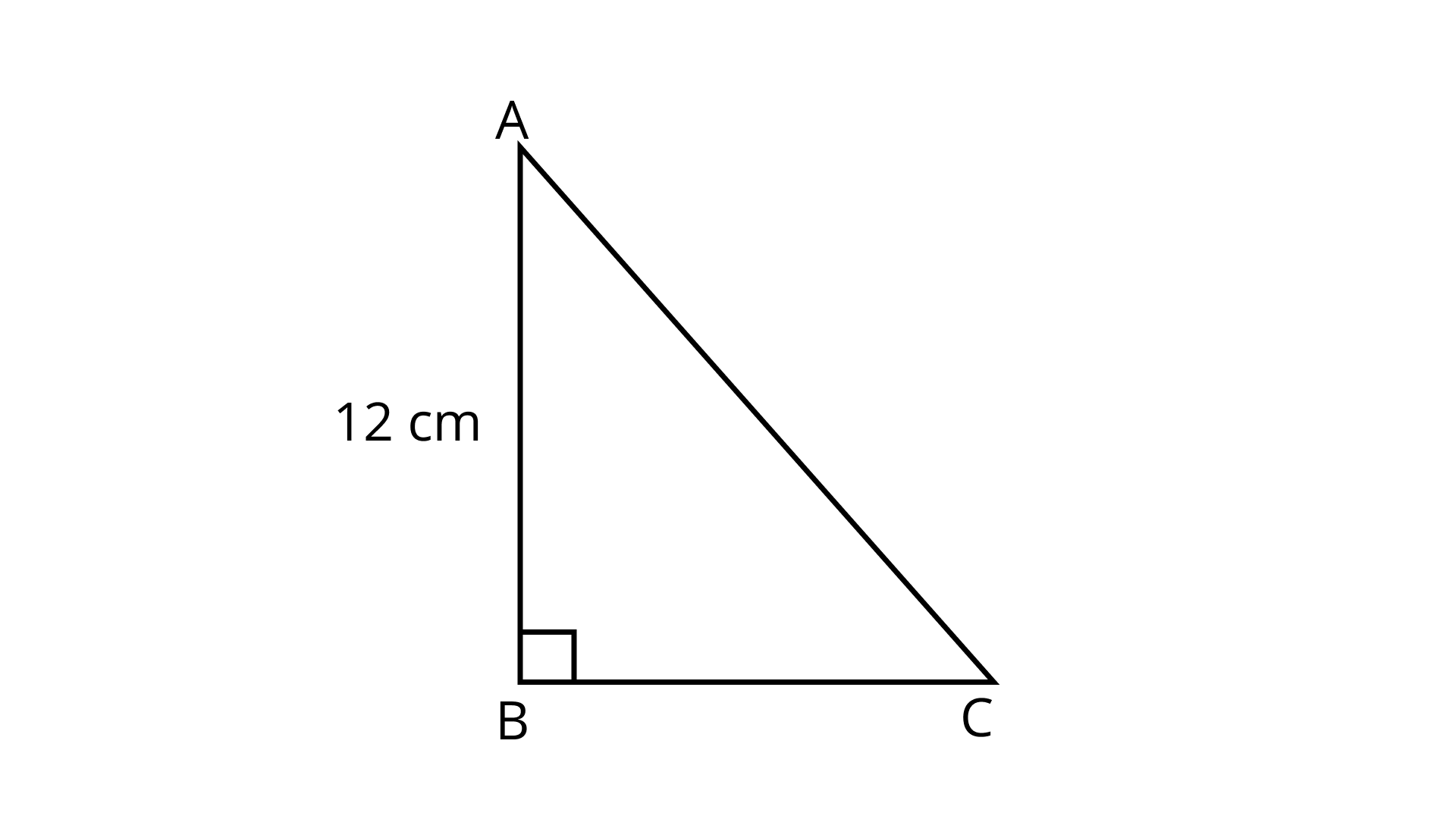
(a) ${\mathbf{18\;cm}}$

(b) ${\mathbf{27\;cm}}$

(c) ${\mathbf{36\;cm}}$

(d) ${\mathbf{54\;cm}}$

Ans: Correct answer is (c).

Given area $ = 54\;{\text{c}}{{\text{m}}^2}$

One of the side $ = 12\;{\text{cm}}$

Let us consider base as $12\;{\text{cm}}$ and height as $x$

Now

Area $ = \dfrac{1}{2} \times b \times h$

$\Rightarrow 54 = \dfrac{1}{2} \times 12 \times h$

$\Rightarrow 54 = 6 \times h$

$\Rightarrow h = \dfrac{{54}}{6}$

$\Rightarrow h = 9$

Now for perimeter we need to find hypotenuse

Thus, by pythagoras

${a^2} + {b^2} = {c^2}$

$\Rightarrow {12^2} + {9^2} = {c^2}$

$\Rightarrow 225 = {c^2}$

Thus, $c = 15$

Now perimeter

$P = a + b + c$

$ = 12 + 9 + 15$

$ = 36cm$

In Examples 3 to 6, fill in the blanks to make it a statement true.

3. Area of parallelogram QPON is ___${\text{c}}{{\text{m}}^2}$.

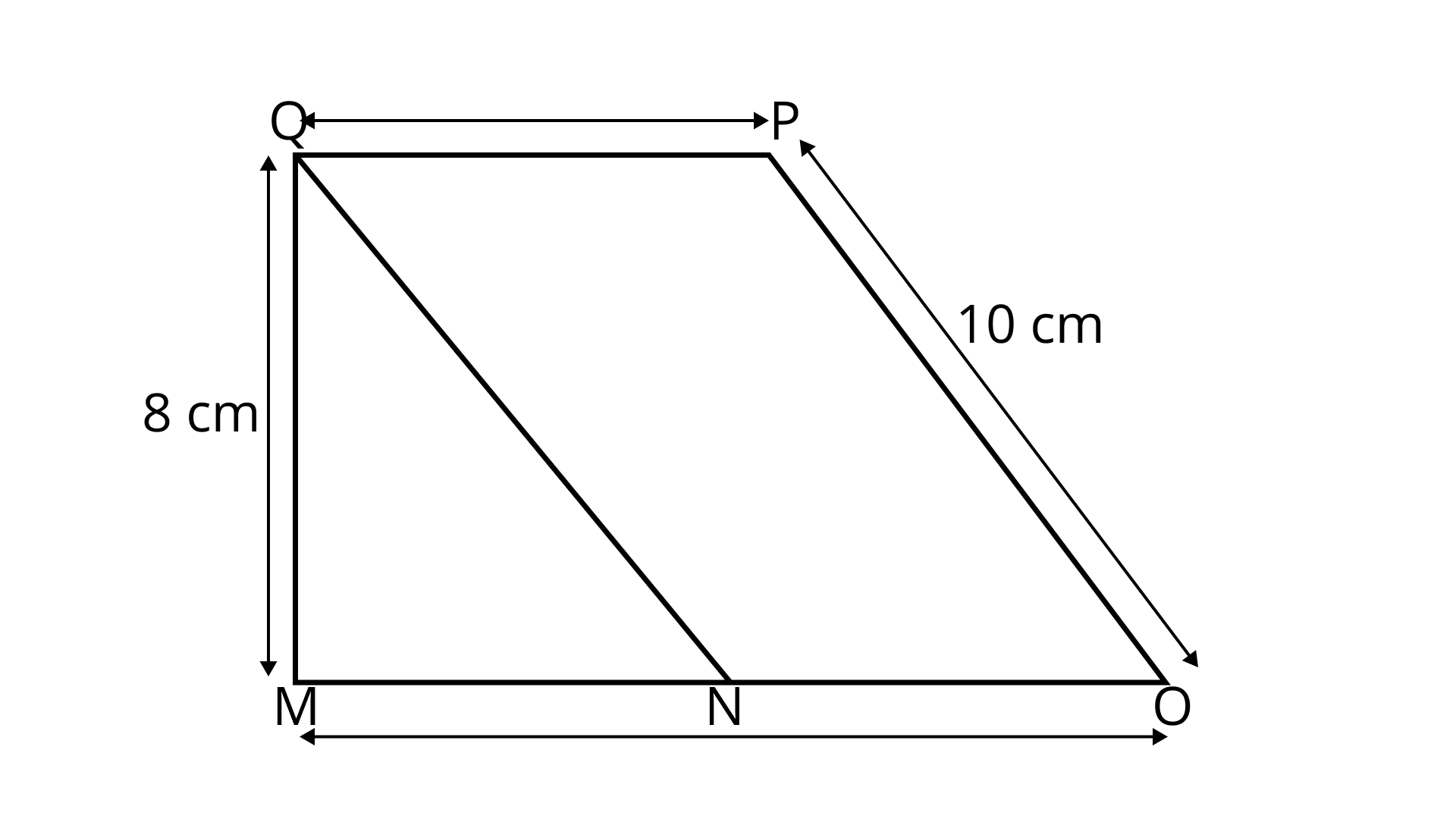
Ans: In a parallelogram, opposite sides are parallel and equal.

$QPON$ is a parallelogram, so $QP = NO = 6\;{\text{cm}}$

Distance between parallel lines $ = QM = 8\;{\text{cm}}$

Area of parallelogram $QPON = $ Parallel side $ \times $ Distance between parallel sides

$ = (6 \times 8){\text{c}}{{\text{m}}^2}$

$ = 48\;{\text{c}}{{\text{m}}^2}$

Hence, Area of parallelogram $\operatorname{QPON} $ is $48\;{\text{c}}{{\text{m}}^2}.$

4. \[{\mathbf{1}}\] hectare = ____________${{\text{cm}}^2}$ 

Ans: $10,00,00,000$

5. ______squares of each side ${\mathbf{1\;m}}$ makes a square of side ${\mathbf{5\;km}}$.

Ans: Area of bigger square $ = (5 \times 5){\text{k}}{{\text{m}}^2} = (5000 \times 5000){{\text{m}}^2}$,

Area of smaller square $ = (1 \times 1){{\text{m}}^2} = 1\;{{\text{m}}^2}$.

Number of squares $ = \dfrac{{(5000 \times 5000)}}{1} = 25000000.$

$2,50,00,000$ squares of each side ${\mathbf{1\;m}}$ makes a square of side ${\mathbf{5\;km}}$.

6. All the congruent triangles have ___area. 

Ans: All the congruent triangles have equal area.

In Examples 7 to 10, state whether the statements are True or False.

7. All the triangles equal in area are congruent.

Ans: The given statement is False

8. The area of any parallelogram ${\mathbf{ABCD}}$, is ${\mathbf{AB \times BC}}$.

Ans: The given statement is False.

9. Ratio of the circumference and the diameter of a circle is more than ${\mathbf{3}}{\mathbf{.}}$

Ans: $=\dfrac{\text{circumference}}{\text{diameter}}=\dfrac{2\pi r}{2r}=\pi=3.14$

Thus the given statement is True.

10. A nursery school playground is ${\mathbf{160\;m}}$ long and ${\mathbf{80\;m}}$ wide. In it ${\mathbf{80\;m \times 80\;m}}$ is kept for swings and in the remaining portion, there is ${\mathbf{1}}{\mathbf{.5\;m}}$ wide path parallel to its width and parallel to its remaining length as shown in Fig. 9.9. The remaining area is covered by grass. Find the area covered by grass.

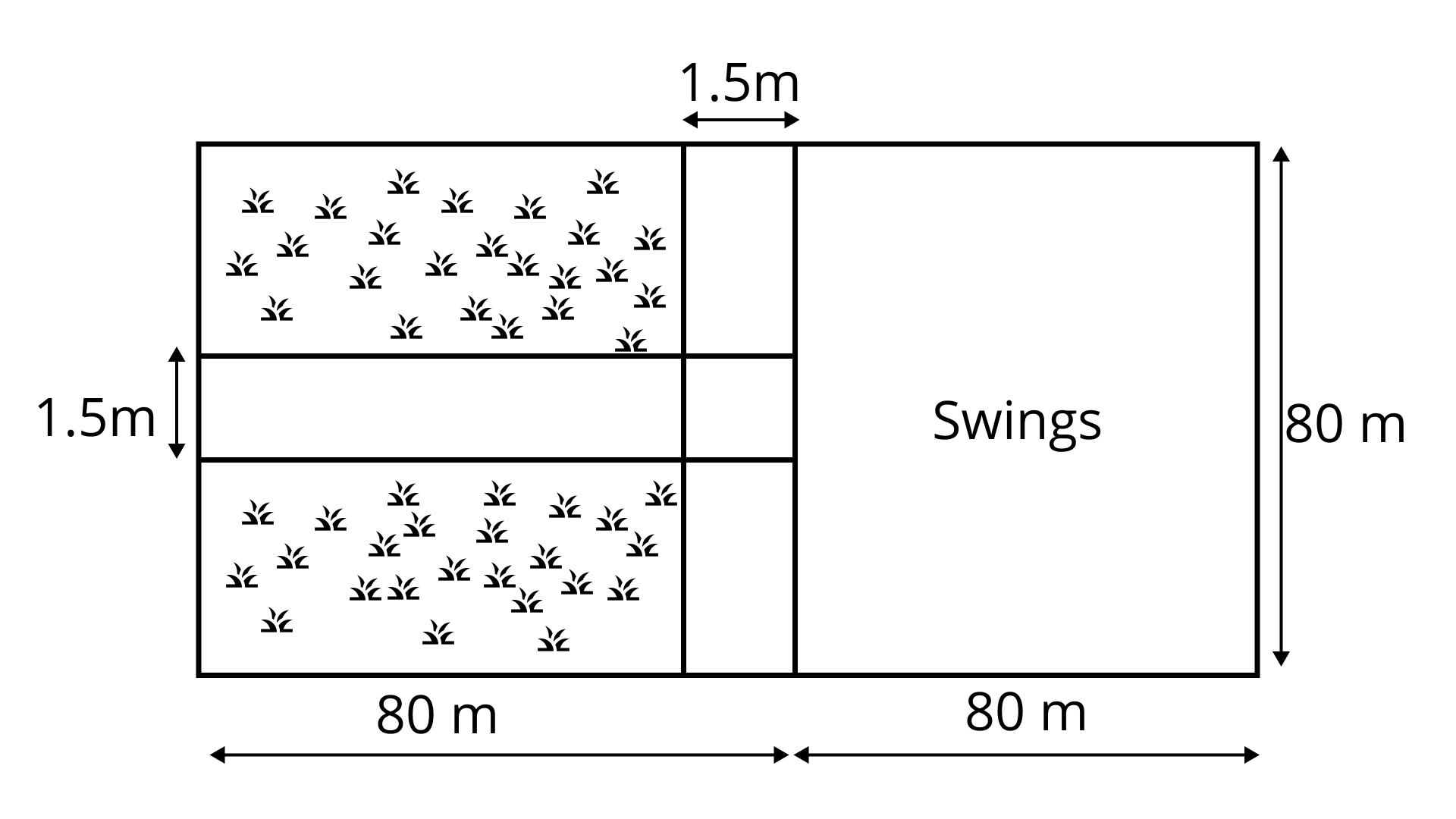
Ans: Area of school playground is $160\;{\text{m}} \times 80\;{\text{m}} = 12800\;{{\text{m}}^2}$

Area kept for swings $ = 80\;{\text{m}} \times 80\;{\text{m}} = 6400\;{{\text{m}}^2}$

Area of path parallel to the width of playground

$ = 80\;{\text{m}} \times 1.5\;{\text{m}} = 120\;{{\text{m}}^2}$

Area of path parallel to the remaining length of playground

$ = 80\;{\text{m}} \times 1.5\;{\text{m}} = 120\;{{\text{m}}^2}.$

Area common to both paths $ = 1.5\;{\text{m}} \times 1.5\;{\text{m}} = 2.25\;{{\text{m}}^2}$.

Total area covered by both the paths

$ = (120 + 120 - 2.25){{\text{m}}^2}$

$ = 237.75{{\text{m}}^2}$

Area covered by grass $ = $ Area of school playground - (Area kept for swings $ + $ Area covered by paths)

$ = 12800\;{{\text{m}}^2} - [6400 + 237.75]{{\text{m}}^2}$

$ = (12800 - 6637.75){{\text{m}}^2}$

$ = 6162.25\;{{\text{m}}^2}.$

11. In Fig. 9.10, ${\mathbf{ABCD}}$ is a parallelogram, in which ${\mathbf{AB = 8\;cm,AD = 6\;cm}}$ and altitude ${\mathbf{AE = 4\;cm}}$. Find the altitude corresponding to side ${\mathbf{AD}}$.

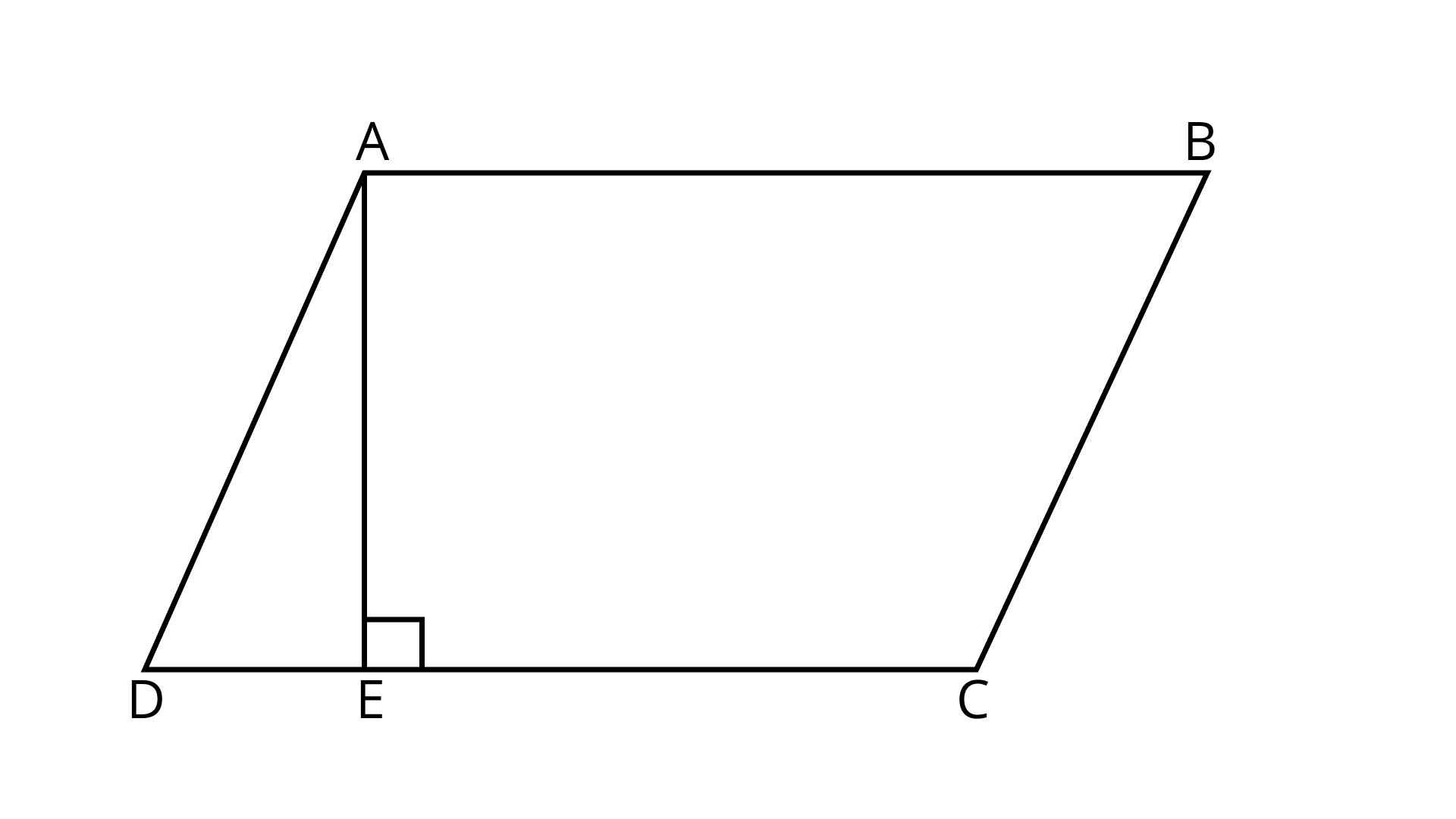
Ans: Area of parallelogram $ABCD = AB \times AE = 8 \times 4\;{\text{c}}{{\text{m}}^2}$ $ = 32\;{\text{c}}{{\text{m}}^2}$

Let altitude corresponding to ${\text{AD}}$ be $h$. Then,

$h \times {\text{AD}} = 32$

$\Rightarrow h \times 6 = 32$

$\Rightarrow h = \dfrac{32}{6} = \dfrac{16}{3}$

Thus, the altitude corresponding to ${\text{AD}}$ is $\dfrac{{16}}{3}\;{\text{cm}}$.

12. A rectangular shaped swimming pool with dimensions ${\mathbf{30\;m \times 20\;m}}$ has ${\mathbf{5\;m}}$ wide cemented path along its length and ${\mathbf{8\;m}}$ wide path along its width (as shown in Fig. 9.11). Find the cost of cementing the path at the rate of Rs \[{\mathbf{200}}\] per ${{\text{m}}^2}$.

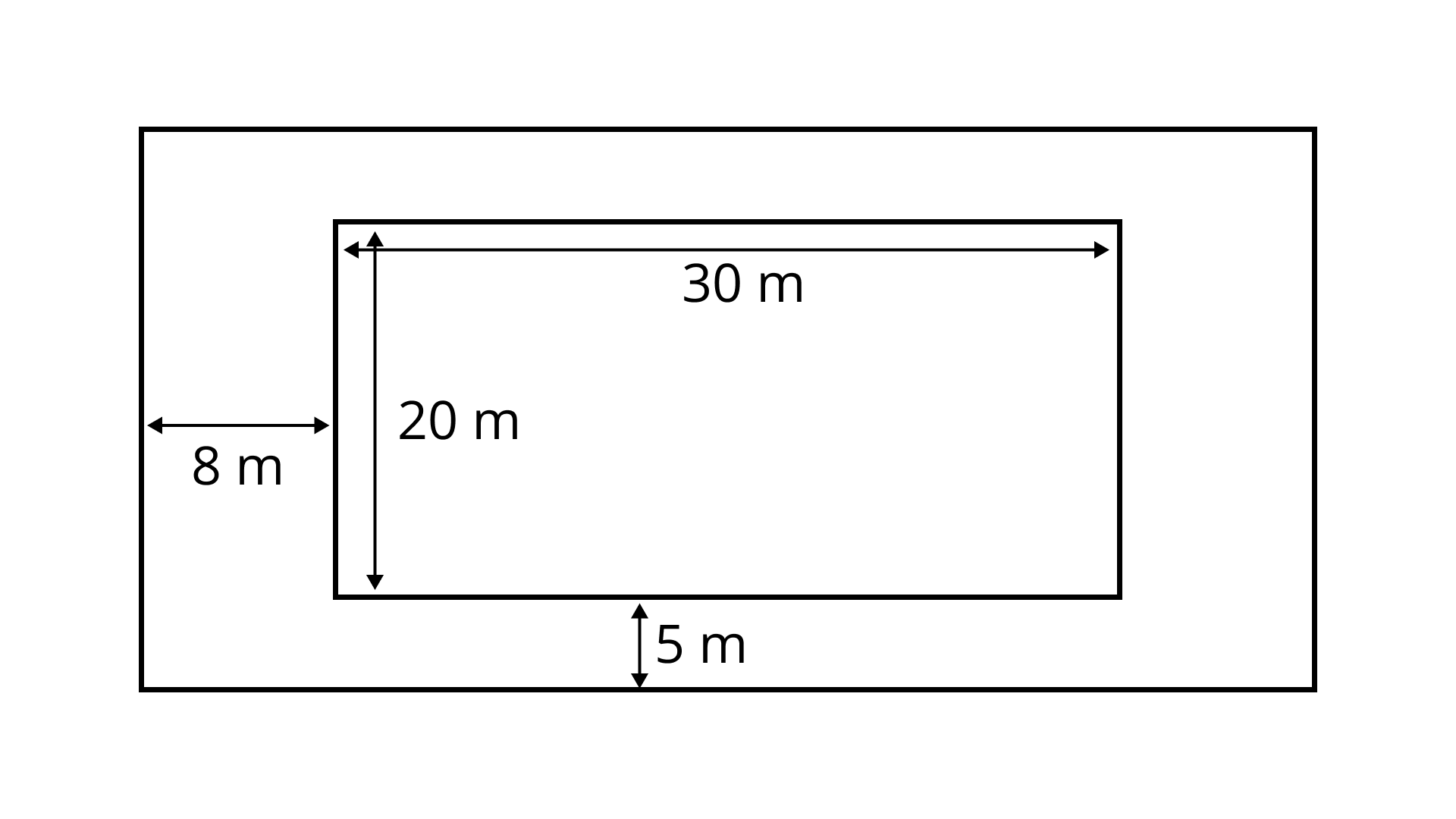
Ans: Area covered by swimming pool $ = 30\;{\text{m}} \times 20\;{\text{m}} = 600\;{{\text{m}}^2}$.

Length of outer rectangle $ = (30 + 8 + 8){\text{m}} = 46\;{\text{m}}$ and its breadth $ = (20 + 5 + 5){\text{m}} = 30\;{\text{m}}$

So, the area of outer rectangle

$ = 46\;{\text{m}} \times 30\;{\text{m}} = 1380\;{{\text{m}}^2}{\text{. }}$

Area of cemented path  =  Area of outer rectangle  -  Area of swimming pool = $(1380 - 600){{\text{m}}^2} = 780\;{{\text{m}}^2}{\text{. }}$

Cost of cementing $1\;{{\text{m}}^2}$ path $ = 200$

So, total cost of cementing the path

$ = 780 \times 200$

$ = 156000$

13. Circumference of a circle is ${\mathbf{33\;cm}}$. Find its area.

Ans: Let the radius of the circle be $r$.

Then, $2\pi r = 33$

So,

$r = \dfrac{{33}}{{2\pi }} = \dfrac{{33}}{2} \times \dfrac{7}{{22}} = \dfrac{{21}}{4}$

Thus, radius is $\dfrac{{21}}{4}\;{\text{cm}}$

So, area of the circle $ = \pi {r^2} = \dfrac{{22}}{7} \cdot \dfrac{{21}}{4} \cdot \dfrac{{21}}{4} = \dfrac{{693}}{8}$

Thus, the area of the circle is $\dfrac{{693}}{8}\;{\text{c}}{{\text{m}}^2}$.

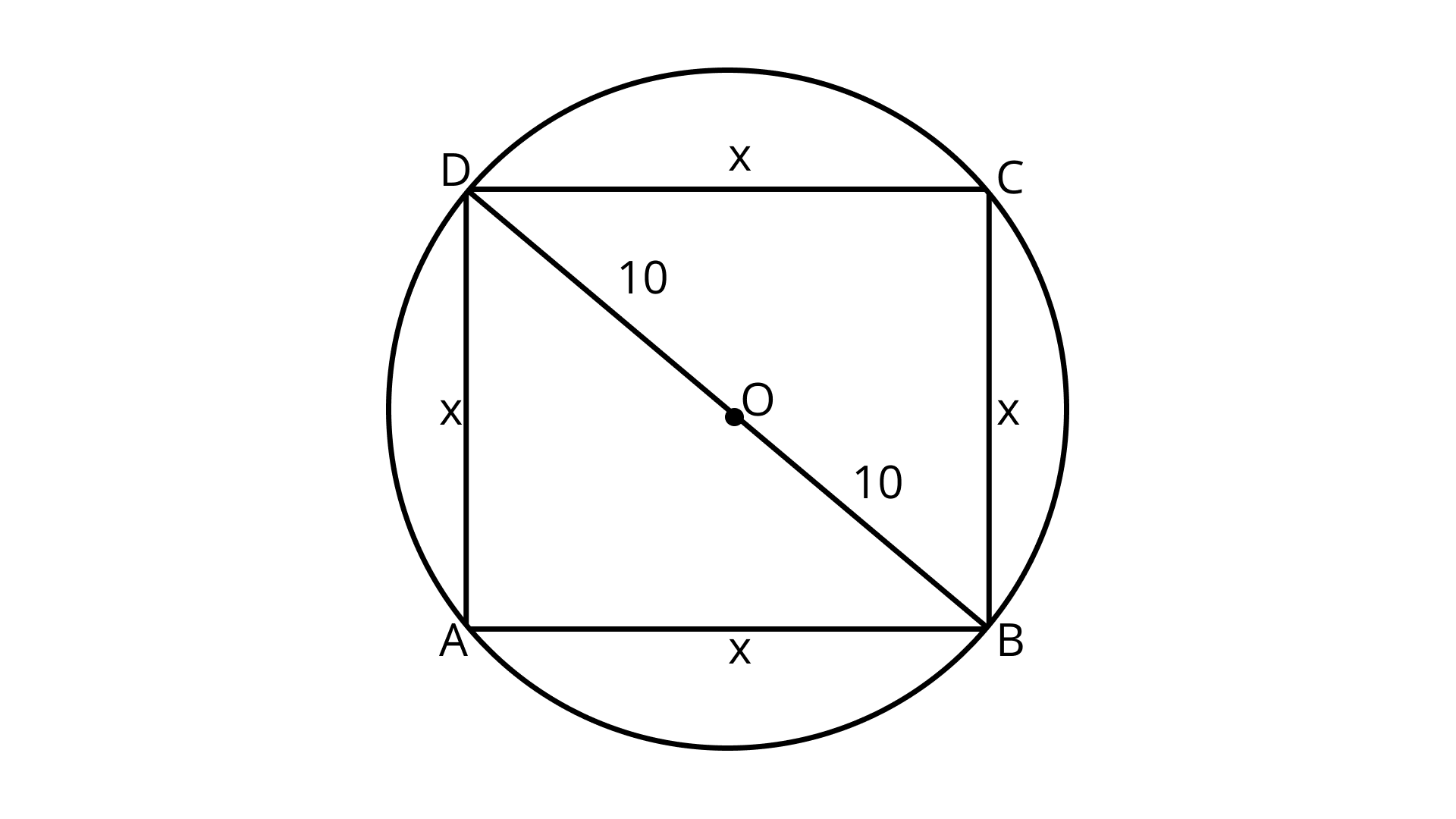
14. Rectangle ${\mathbf{ABCD}}$ is formed in a circle as shown in Fig. 9.12. If  ${\mathbf{AE = 8\;cm}}$ and ${\mathbf{AD = 5\;cm}}$, find the perimeter of the rectangle.

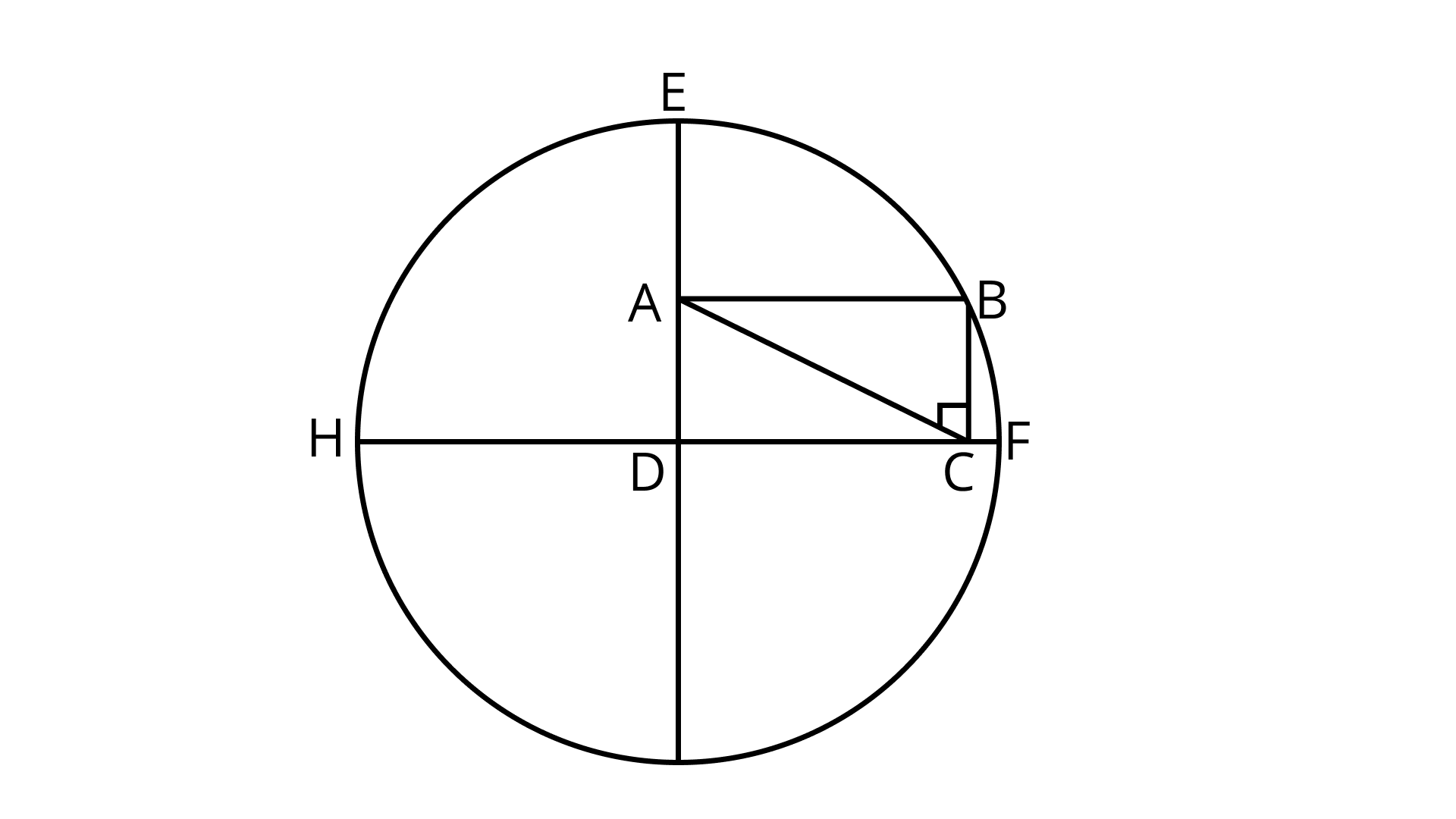
Ans: ${\text{DE}} = {\text{EA}} + {\text{AD}} = (8 + 5)cm = 13cm$

DE is the radius of the circle.

Also, DB is the radius of the circle.

Next, ${\text{AC}} = {\text{DB}}$ 

Therefore, ${\text{AC}} = 13\;{\text{cm}}.$

From $\vartriangle {\text{ADC}}$,

${\text{D}}{{\text{C}}^2}= {\text{A}}{{\text{C}}^2} - {\text{A}}{{\text{D}}^2}$

$= {13^2} - {5^2}$

$= 169 - 25$

$=144 = {12^2}$

So, ${\text{DC}} = 12$

Thus, length of ${\text{DC}}$ is $12\;{\text{cm}}.$

Hence, perimeter of the rectangle ${\text{ABCD}}$

$ = 2(12 + 5){\text{cm}} = 34\;{\text{cm}}.$

15. Find the area of a parallelogram-shaped shaded region of Fig. 9.13. Also, find the area of each triangle. What is the ratio of the area of the shaded portion to the remaining area of the rectangle?

Ans: In DEBF the base is FB and height is AD.

We know area of a parallelogram is base $\times$ height

Area of DEBF = FB $\times \text { AD }$

$=(10-4) \mathrm{cm} \times 6 \mathrm{~cm}$

$=6 \mathrm{~cm} \times 6 \mathrm{~cm}$

$=36 \mathrm{~cm}^2$

In DAF the base is AF and height is AD

Area of a triangle = $\dfrac{1}{2}$ $\times$ base $\times$ height

$=\dfrac{1}{2}\times 4 \times 6 \mathrm{~cm}$

$=12 \mathrm{~cm}^2$

In BCE the base is EC and height is CB

Area of a triangle = $\dfrac{1}{2}$ $\times$ base $\times$ height

$=\dfrac{1}{2}\times 4 \times 6 \mathrm{~cm}$

$=12 \mathrm{~cm}^2$

Area of each triangle is $12 \mathrm{~cm}^2$.

Area of unshaded part $=12 \mathrm{~cm}^2+12 \mathrm{~cm}^2$

$=24 \mathrm{~cm}^2$

The ratio of shaded part to the leftover area in the rectangle is $36: 24$ $=3: 2$

Exercise

In the Questions 1 to 37, there are four options, out of which one is correct. Choose the correct one.

1. Observe the shapes ${\mathbf{1,2,3}}$ and 4 in the figures. Which of the following statements is not correct?

(a) Shapes 1,3 and 4 have different areas and different perimeters.

(b) Shapes 1 and 4 have the same area as well as the same perimeter.

(c) Shapes 1,2 and 4 have the same area.

(d) Shapes 1,3 and 4 have the same perimeter.

Ans: Option (a) is correct.

Perimeter of the shape 1

$ = 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 10 + 1 + 1 = 22{\text{ units}}$

Therefore, area is

$ = 18 \times 1 = 18{\text{ units}}{{\text{ }}^2}$

Perimeter of the shape 2

$ = 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 = 18{\text{ units  }}$

${\text{Therefore,  area is }} = 18 \times 1 = 18{\text{ unit}}{{\text{s}}^2}$

Perimeter of the shape 3

$ = 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1$

$ = 22{\text{ units }}$

Therefore, area is

$ = 16 \times 1$

$ = 16{\text{ units}}{{\text{ }}^2}$

Perimeter of the shape 4

$ = 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 = 22{\text{ units }}$

Therefore, area is

$ = 18 \times 1 = 18{\text{ unit}}{{\text{s}}^2}$

2. A rectangular piece of dimensions $3\;{\text{cm}} \times 2\;{\text{cm}}$ was cut from a rectangular sheet of paper of dimensions $6\;{\text{cm}} \times 5\;{\text{cm}}$ (Fig. 9.14).

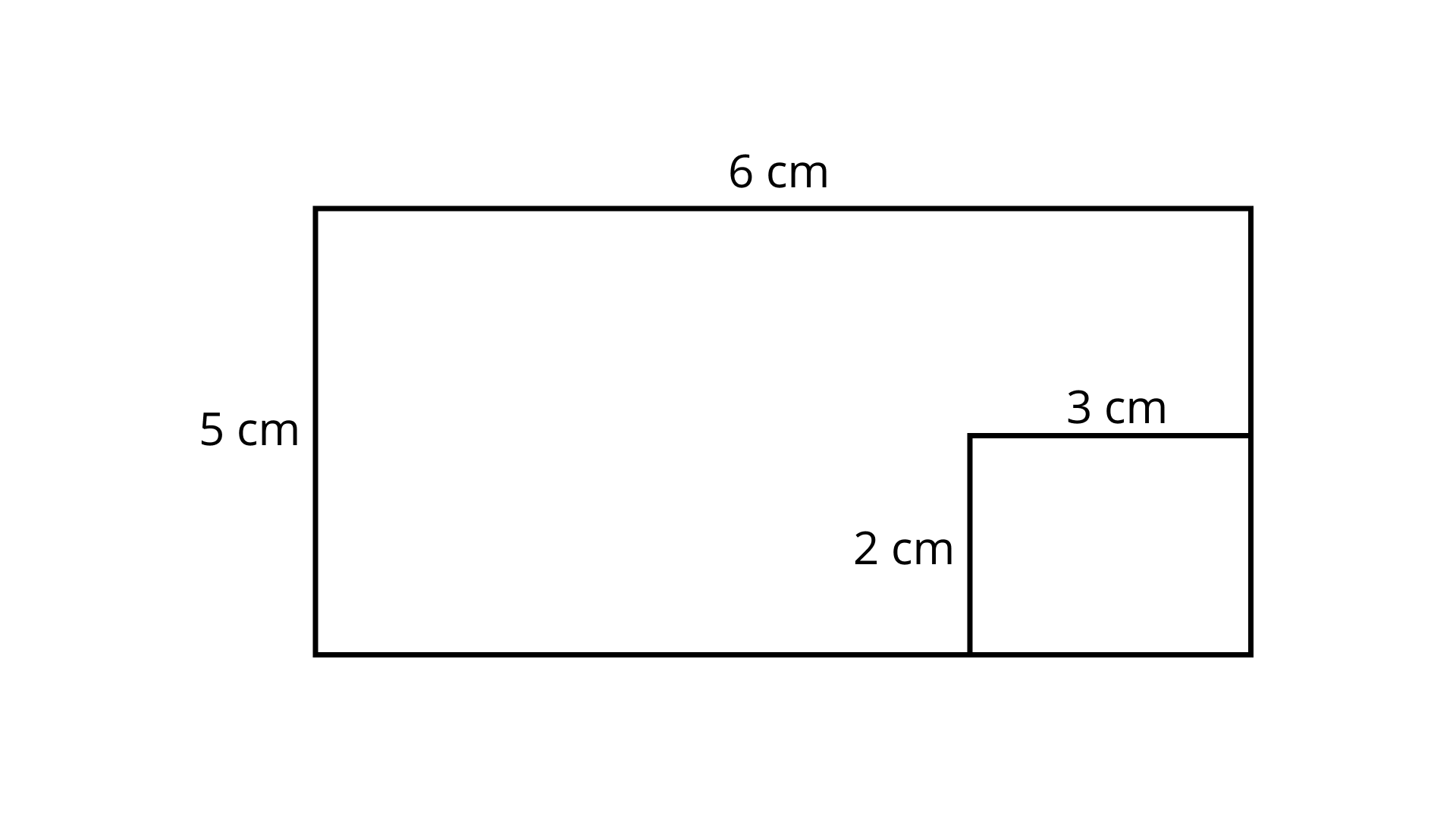
Area of remaining sheet of paper is

(a) ${\mathbf{30}}\;{\mathbf{c}}{{\mathbf{m}}^{\mathbf{2}}}$

(b) ${\mathbf{36\;c}}{{\mathbf{m}}^{\mathbf{2}}}$

(c) ${\mathbf{24\;c}}{{\mathbf{m}}^{\mathbf{2}}}$

(d) ${\mathbf{22\;c}}{{\mathbf{m}}^{\mathbf{2}}}$

Ans: Option (c) is correct.

Given,

Area of bigger rectangle $ = (6 \times 5){\text{cm}} = 30\;{\text{c}}{{\text{m}}^2}$

Area of smaller rectangle $ = (3 \times 2){\text{cm}} = 6\;{\text{c}}{{\text{m}}^2}$

So, area of remaining sheet of paper \[ = \] Area of bigger rectangle -Area of smaller rectangle $ = (30 - 6) = 24\;{\text{c}}{{\text{m}}^2}$

3. ${\mathbf{36}}$ unit squares are joined to form a rectangle with the least perimeter. Perimeter of the rectangle is

(a) ${\mathbf{12}}$ units

(b)${\mathbf{26}}$ units

(c) ${\mathbf{24}}$units

(d)$\mathbf{36}$ units

Ans: Option (b) is correct.

Area of rectangle is \[36\] units

$ \Rightarrow 36 = 6 \times 6$

$ = 2 \times 3 \times 3 \times 2$

$ = 4 \times 9$

Therefore, the sides of a rectangle are $4\;{\text{cm}}$ and $9\;{\text{cm}}$. 

Perimeter $ = 2(l + b)$

$ = 2(4 + 9)$

$ = 13 \times 2$

$ = 26$ units

4. A wire is bent to form a square of side ${\mathbf{22\;cm}}$. If the wire is rebent to form a circle, its radius is

(a) ${\mathbf{22\;cm}}$

(b) ${\mathbf{14\;cm}}$

(c) ${\mathbf{11\;cm}}$

(d) ${\mathbf{7\;cm}}$

Ans: Option (b) is correct.

Given, side of a square is $22\;{\text{cm}}$

The wire has the same length. 

Hence, the perimeter of the square and circumference of the circle are equal.

Circumference of circle $ = $ Perimeter of square

$ \Rightarrow 2 \times \pi  \times r = 4 \times \left( {side} \right)$ 

$ \Rightarrow 2 \times \dfrac{{22}}{7} \times r = 4 \times 22$ 

$ \Rightarrow r = \dfrac{{4 \times 22 \times 7}}{{2 \times 22}}$ 

$ \Rightarrow r = 14{\text{cm}}$

So, $14\;{\text{cm}}$ is the radius of the circle.

5. Area of the circle obtained in Question 4 is

(a) ${\mathbf{196\;c}}{{\mathbf{m}}^{\mathbf{2}}}$

(b) ${\mathbf{212\;c}}{{\mathbf{m}}^{\mathbf{2}}}$

(c) ${\mathbf{616\;c}}{{\mathbf{m}}^{\mathbf{2}}}$

(d) ${\mathbf{644\;c}}{{\mathbf{m}}^{\mathbf{2}}}$

Solution: Option (c) is correct.

Area of the circle

$ = \pi {r^2}$ 

$ = \dfrac{{22}}{7} \times 14 \times 14$

$ = 616\;{\text{c}}{{\text{m}}^2}$

6. Area of a rectangle and the area of a circle are equal. If the dimensions of the rectangle are ${\mathbf{14\;cm \times 11\;cm}}$, then radius of the circle is

(a) ${\mathbf{21\;cm}}$

(b) ${\mathbf{10}}{\mathbf{.5\;cm}}$

(c) ${\mathbf{14\;cm}}$

(d) ${\mathbf{7\;cm}}$.

Ans: Option (d) is correct.

Given,

Length of rectangle $ = 1 = 14\;{\text{cm}}$

Breadth of rectangle $ = b = 11\;{\text{cm}}$

Area of circle $ = $ Area of rectangle

$ \Rightarrow \pi {r^2} = l \times b$

$ \Rightarrow \dfrac{{22}}{7} \times {r^2} = 14 \times 11$

$ \Rightarrow {r^2} = \dfrac{{14 \times 11 \times 7}}{{22}}$

$ \Rightarrow r = \sqrt {49} $

$ \Rightarrow r = 7{\text{cm}}$

7. Area of shaded portion in Fig. 9.15 is 

(a) ${\mathbf{25}}\;{\mathbf{c}}{{\mathbf{m}}^{\mathbf{2}}}$

(b) ${\mathbf{15c}}{{\mathbf{m}}^{\mathbf{2}}}$

(c) ${\mathbf{14c}}{{\mathbf{m}}^{\mathbf{2}}}$

(d) ${\mathbf{10c}}{{\mathbf{m}}^{\mathbf{2}}}$

Ans: Option (d) is correct.

From the given figure,

Length of rectangle $ = 1 = 5\;{\text{cm}}$

Breadth of rectangle $ = b = 3 + 1 = 4\;{\text{cm}}$

Thus, area of shaded portion $ = \dfrac{1}{2} \times $ area of rectangle 

$ = \dfrac{1}{2} \times l \times b$

$ = \dfrac{1}{2} \times 5 \times 4$

$ = 10\;{\text{c}}{{\text{m}}^2}$

8. Area of parallelogram ${\text{ABCD}}$ (Fig. 9.16) is not equal to

(a) ${\mathbf{DE \times DC}}$

(b) ${\mathbf{BE \times AD}}$

(c) ${\mathbf{BF \times DC}}$

(d) ${\mathbf{BE \times BC}}$

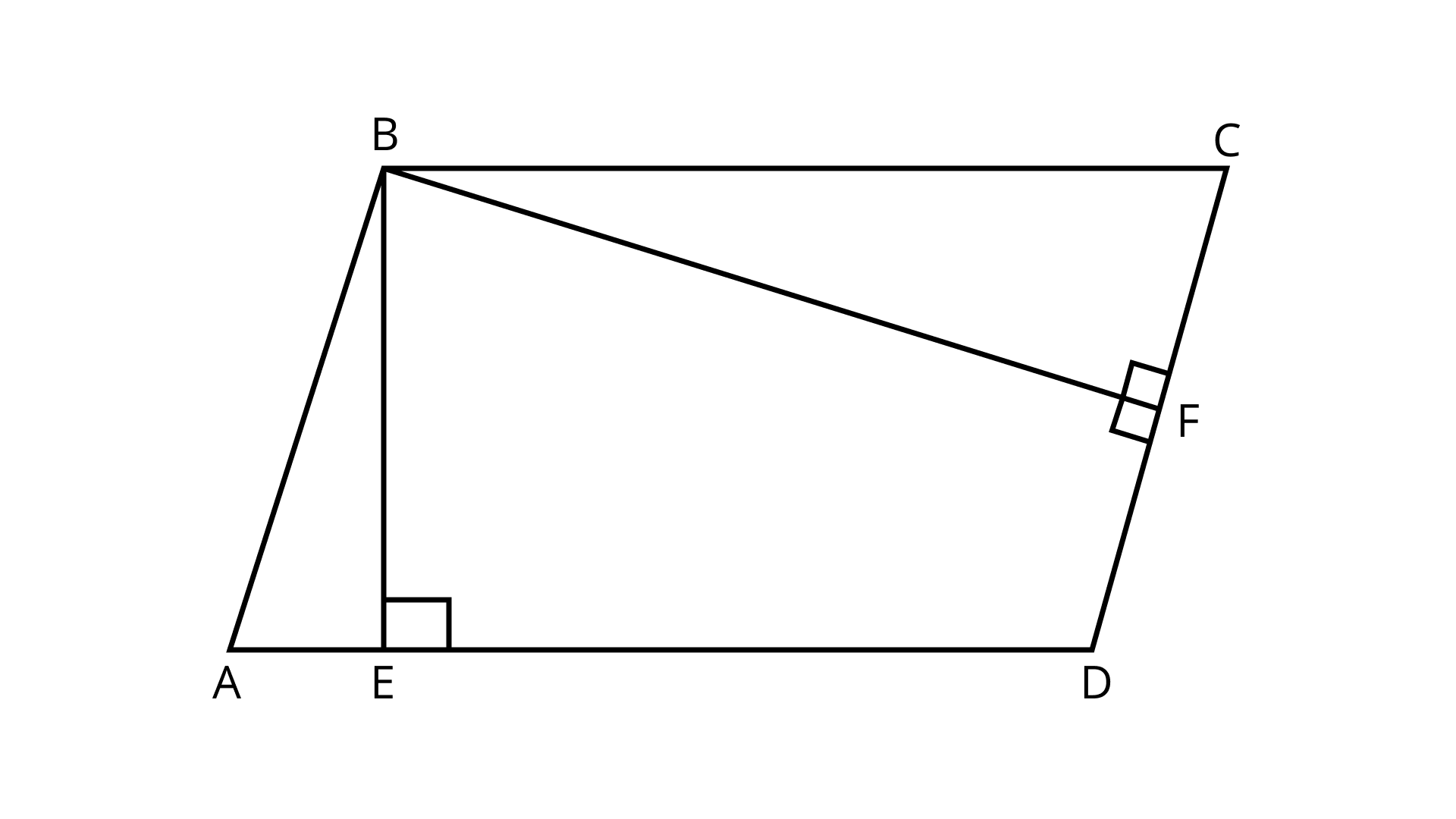
Ans: Option (a) is correct.

Area of parallelogram = Base $\times$ height (or altitude)

Here, the perpendicular dropped on the side from the opposite vertex is known as height 

So, the area of parallelogram \[ABCD = AD \times HE\]

$ = {\text{BC}} \times {\text{BE}}$

$= {\text{DC}} \times {\text{BF}}$

Hence, (a) is the correct answer.

9. Area of triangle MNO of Fig is

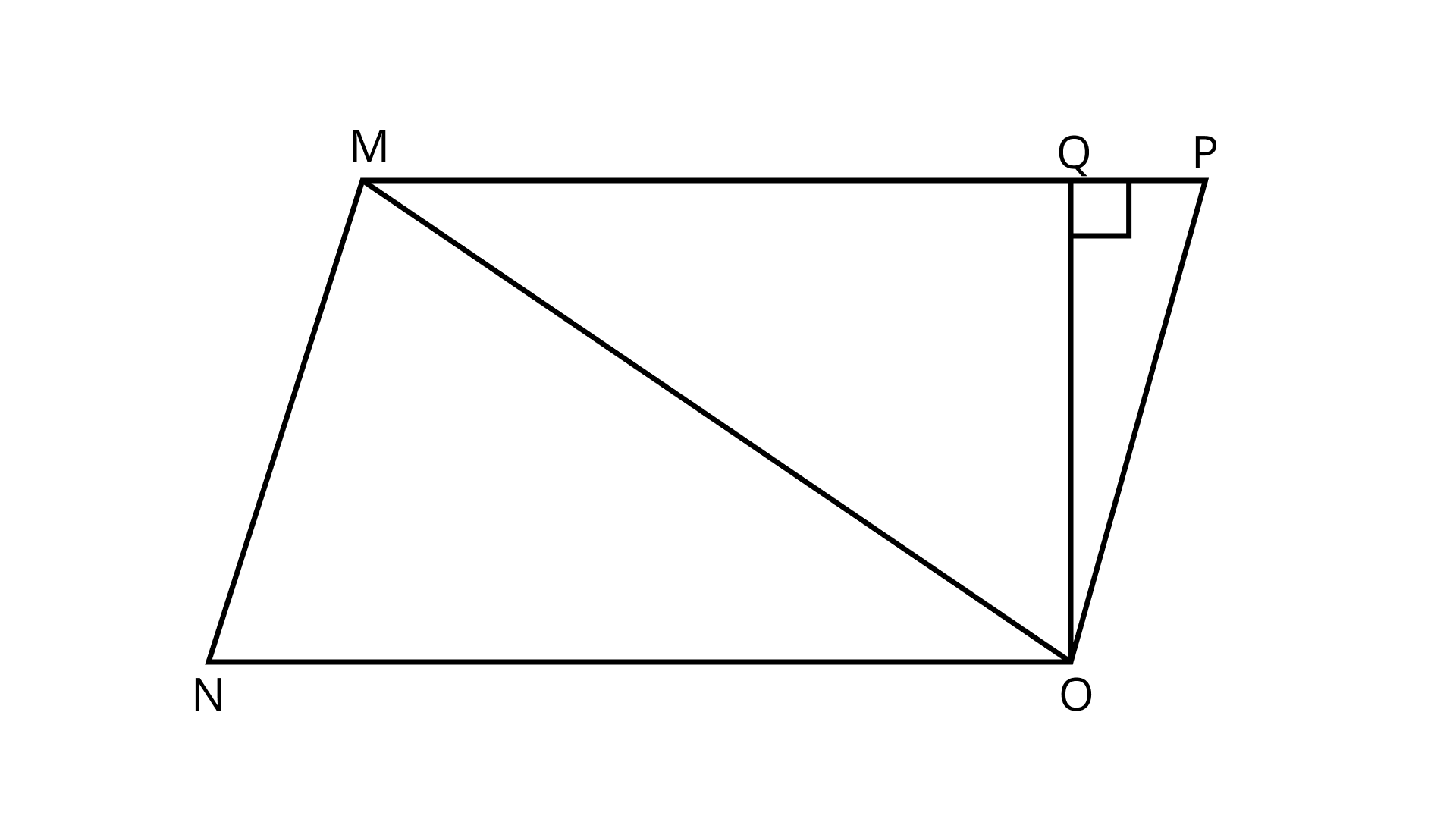
(a) $\dfrac{{\mathbf{1}}}{{\mathbf{2}}}{\mathbf{MN \times NO}}$

(b) $\dfrac{{\mathbf{1}}}{{\mathbf{2}}}{\mathbf{NO \times MO}}$

(c) $\dfrac{{\mathbf{1}}}{{\mathbf{2}}}{\mathbf{MN \times OQ}}$

(d) $\dfrac{{\mathbf{1}}}{{\mathbf{2}}}{\mathbf{NO \times OQ}}$

Ans: Option (d) is correct

As we know that,

Area of triangle $ = \dfrac{1}{2} \times $ base $ \times $ height

$ = \dfrac{1}{2} \times NO \times OQ$

10. Ratio of area of triangle MNO to the area of parallelogram MNOP in the same figure is

(a) \[{\mathbf{2}}:{\mathbf{3}}\]

(b) ${\mathbf{1}}:{\mathbf{1}}$

(c) ${\mathbf{1}}:{\mathbf{2}}$

(d) ${\mathbf{2}}:{\mathbf{1}}$

Ans: Option (c) is correct.

Area of triangle MNO: Area of parallelogram MNOP

$ = \dfrac{{\dfrac{1}{2} \times {\text{base}} \times {\text{height}}}}{{{\text{Base}} \times {\text{corresponding height}}}}$

$ = 1:2$

Therefore, \[1:2\] is the required ratio.

11. Ratio of areas of ${\mathbf{\Delta MNO,\Delta MOP}}$ and ${\mathbf{\Delta MPQ}}$ in Fig. is 

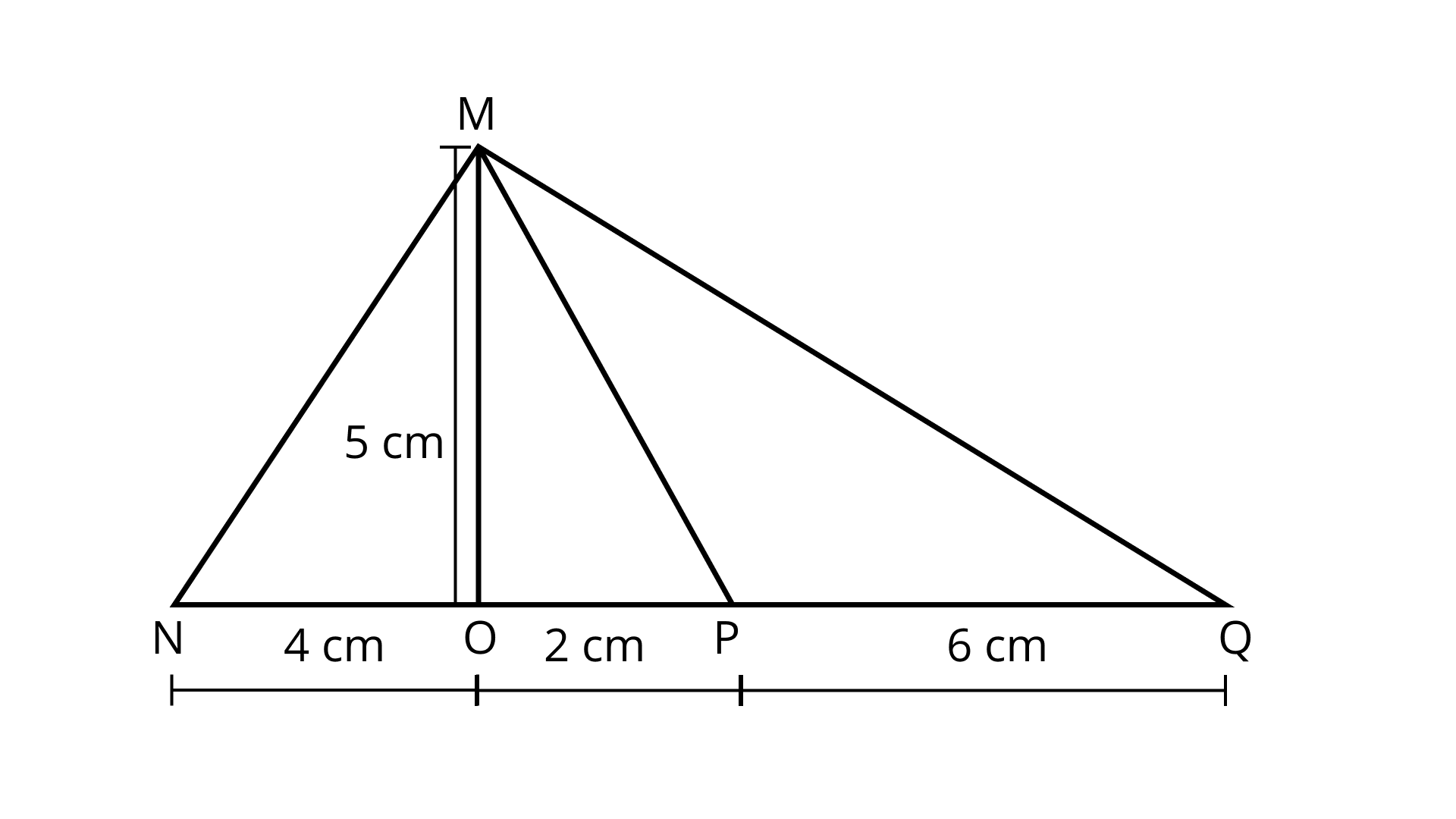
(a) \[{\mathbf{2}}:{\mathbf{1}}:{\mathbf{3}}\]

(b) \[{\mathbf{1}}:{\mathbf{3}}:{\mathbf{2}}\]

(c) \[{\mathbf{2}}:{\mathbf{3}}:{\mathbf{1}}\]

(d) \[{\mathbf{1}}:{\mathbf{2}}:{\mathbf{3}}\]

Ans: Option (a) is correct.

Area of $\Delta MNO = \dfrac{1}{2} \times NO \times MO$ 

$ = \dfrac{1}{2} \times 4 \times 5 = 10\;{\text{c}}{{\text{m}}^2}$ 

${\text{ Area of }}\Delta {\text{MOP }} = \dfrac{1}{2} \times {\text{ OP }} \times {\text{ MO }}$

$ = \dfrac{1}{2} = 2 \times 5 = 5{\text{ cm}}{{\text{ }}^2}$

Area of $\Delta MPQ = \dfrac{1}{2} \times QP\; \times MO$ 

$ = \dfrac{1}{2} \times 6 \times 5 = 15\;{\text{c}}{{\text{m}}^2}$

Now, Area of $\Delta MNO$: Area of $\Delta MOP$: Area of $\Delta MPQ$=10:5:15=2:1:3

Hence, (a) is the correct answer.

12. In Fig. ${\mathbf{9}}{\mathbf{.19,EFGH}}$ is a parallelogram, altitudes ${\mathbf{FK}}$ and \[FI\] are ${\mathbf{8\;cm}}$ and ${\mathbf{4\;cm}}$ respectively. If ${\mathbf{EF = 10\;cm}}$, then area of ${\mathbf{EFGH}}$ is

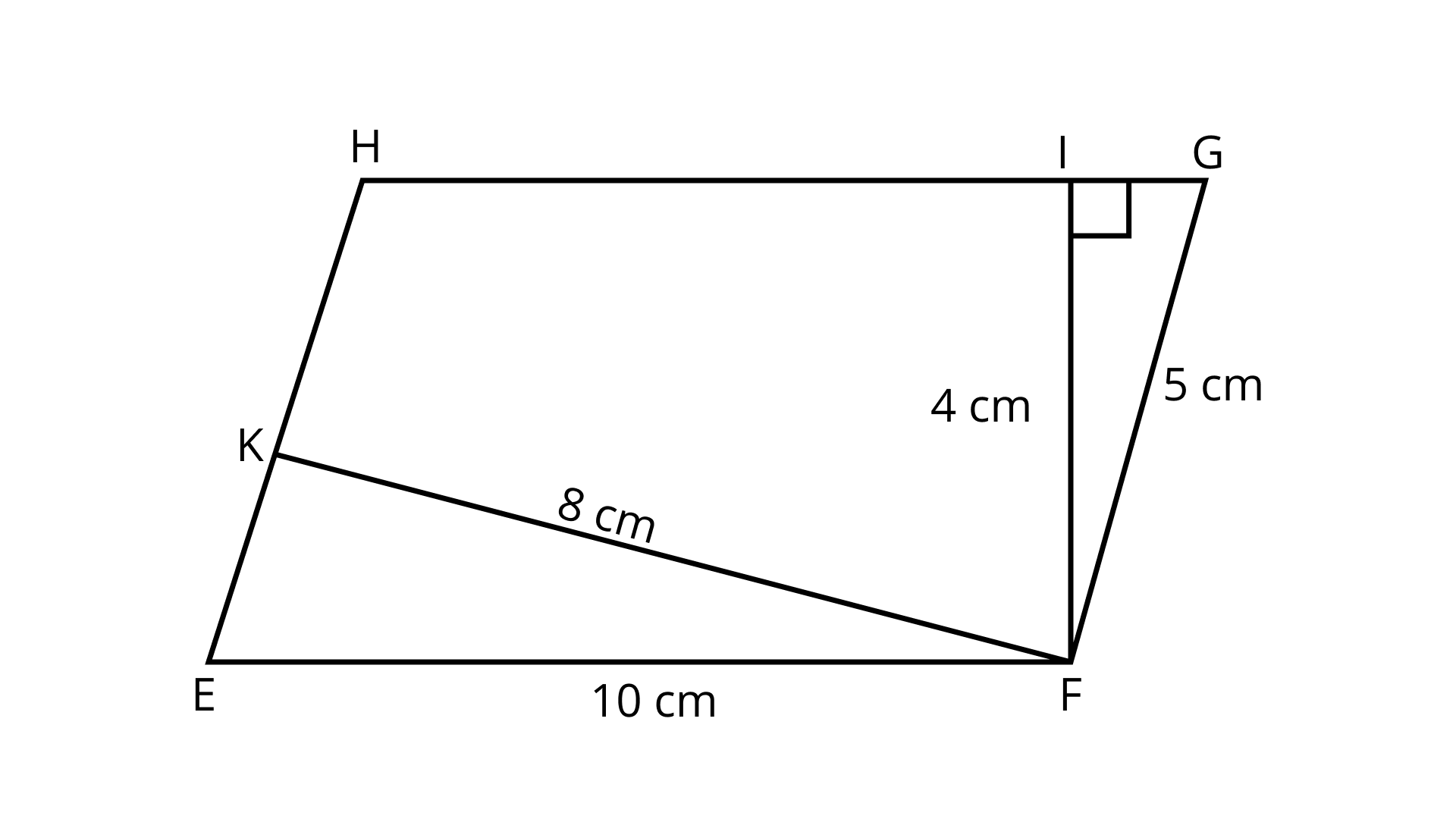
(a) ${\mathbf{20\;c}}{{\mathbf{m}}^{\mathbf{2}}}$

(b) ${\mathbf{32\;c}}{{\mathbf{m}}^{\mathbf{2}}}$

(c) ${\mathbf{40\;c}}{{\mathbf{m}}^{\mathbf{2}}}$

(d) ${\mathbf{80\;c}}{{\mathbf{m}}^{\mathbf{2}}}$

Ans: Option (c) is correct.

Area of parallelogram $({\text{EFGH}}) = $ Base $ \times $ corresponding height

$ = 10 \times 4$

$ = 40\;{\text{c}}{{\text{m}}^2}$

13. In reference to a circle the value of ${\mathbf{\pi }}$ is equal to

(a) $\dfrac{{{\mathbf{ area }}}}{{{\mathbf{ circumference }}}}$

(b) $\dfrac{{{\mathbf{ area }}}}{{{\mathbf{ diameter }}}}$

(c) $\dfrac{{{\mathbf{ circumference }}}}{{{\mathbf{ diameter }}}}$

(d) $\dfrac{{{\mathbf{ circumference }}}}{{{\mathbf{ radius }}}}$

Ans: Option (c) is correct.

As we know,

Circumference of a circle $ = 2\pi r$

Circumference $ = \pi  \times $ Diameter

$\pi  = \dfrac{{{\text{ circumference }}}}{{{\text{ diameter }}}}$

14. Circumference of a circle is always

(a) more than three times of its diameter

(b) three times of its diameter

(c) less than three times of its diameter

(d) three times of its radius

Ans: Option (a) is correct.

As we know that,

Circumference of a circle $ = 2\pi r$

Circumference $ = 2 \times 3.14 \times r$

Circumference $ = 3.14 \times d$

Therefore, Circumference of a circle is more than three of its diameter.

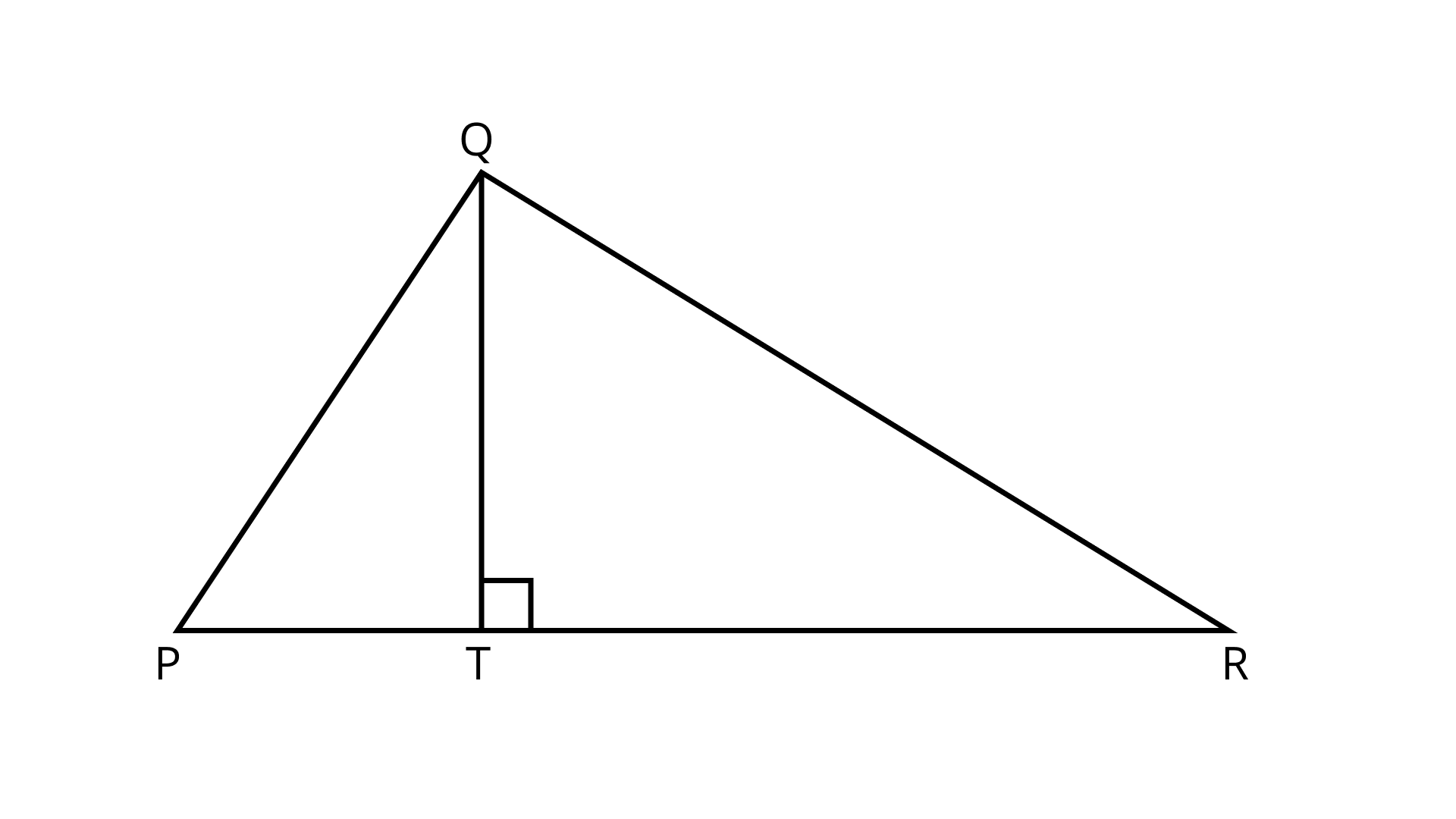
15. Area of triangle ${\mathbf{PQR}}$ is ${\mathbf{100\;c}}{{\mathbf{m}}^{\mathbf{2}}}$ (Fig. 9.20). If altitude ${\mathbf{QT}}$ is ${\mathbf{10\;cm}}$, then its base PR is

(a) ${\mathbf{20\;cm}}$

(b) ${\mathbf{15\;cm}}$

(c) ${\mathbf{10\;cm}}$

(d) ${\mathbf{5\;cm}}$

Ans: Option (a) is correct.

Given, area of triangle ${\text{PQR}} = 100\;{\text{c}}{{\text{m}}^2}$

We know that,

Area of triangle ${\text{PQR}} = \dfrac{1}{2} \times PR \times QT$

$ \Rightarrow 100 = \dfrac{1}{2} \times PR \times 10$

$ \Rightarrow PR = \dfrac{{100 \times 2}}{{10}}$

$ \Rightarrow PR = 20\;{\text{cm}}$

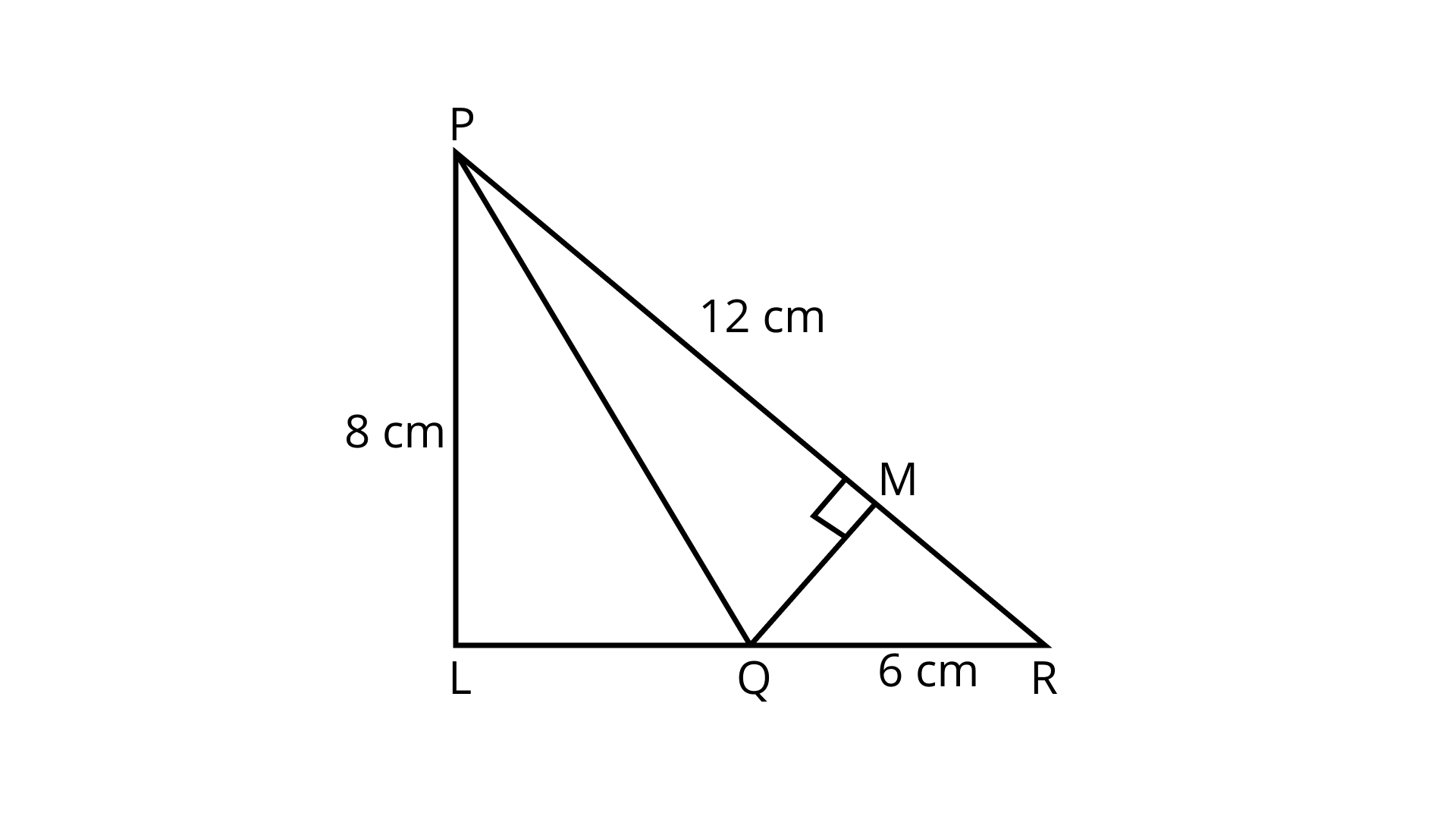
16. In Fig. 9.21, if ${\mathbf{PR = 12\;cm,QR = 6\;cm}}$ and  ${\mathbf{PL = 8\;cm}}$, then $QM$ is

(a) ${\mathbf{6\;cm}}$

(b) ${\mathbf{9\;cm}}$

(c) ${\mathbf{4\;cm}}$

(d) ${\mathbf{2\;cm}}$

Ans: Option (c) is correct.

Given that,

$PL = 8{\text{cm }}$

$PR = 12{\text{cm}}$

$QR = 6{\text{cm }}$

Now, in right-angled triangle PLR Using Pythagoras theorem,

$ \Rightarrow P{R^2} = P{L^2} + L{R^2}$

$ \Rightarrow L{R^2} = 144 - 64$

$ \Rightarrow LR = \sqrt {80}  = 4\sqrt 5 \;{\text{cm}}$

$LR = LQ + QR$

$ \Rightarrow LQ = LR - QR = (4\sqrt 5  - 6)CM$

Now, area of triangle PLR

${A_1} = \dfrac{1}{2} \times (4\sqrt 5 ) \times 8$

$ = 16\sqrt 5 \;{\text{c}}{{\text{m}}^2}$

Now, area of triangle PLQ

${A_1} = \dfrac{1}{2} \times (4\sqrt 5  - 6) \times 8$

$ = (16\sqrt 5  - 24){\text{c}}{{\text{m}}^2}$

Hence, area of triangle \[PLR{\text{ }} = \]Area of triangle \[PLQ{\text{ }} + \]Area of triangle \[PQR\]

$ \Rightarrow 16\sqrt 5  = (16\sqrt 5  - 24) + $ Area of triangle $PQR$

$ \Rightarrow $ Area of triangle $PQR = 24\;{\text{c}}{{\text{m}}^2}$

$ \Rightarrow \dfrac{1}{2} \times PR \times QM = 24$

$ \Rightarrow \dfrac{1}{2} \times 12 \times QM = 24$

$QM = 4\;{\text{cm}}$

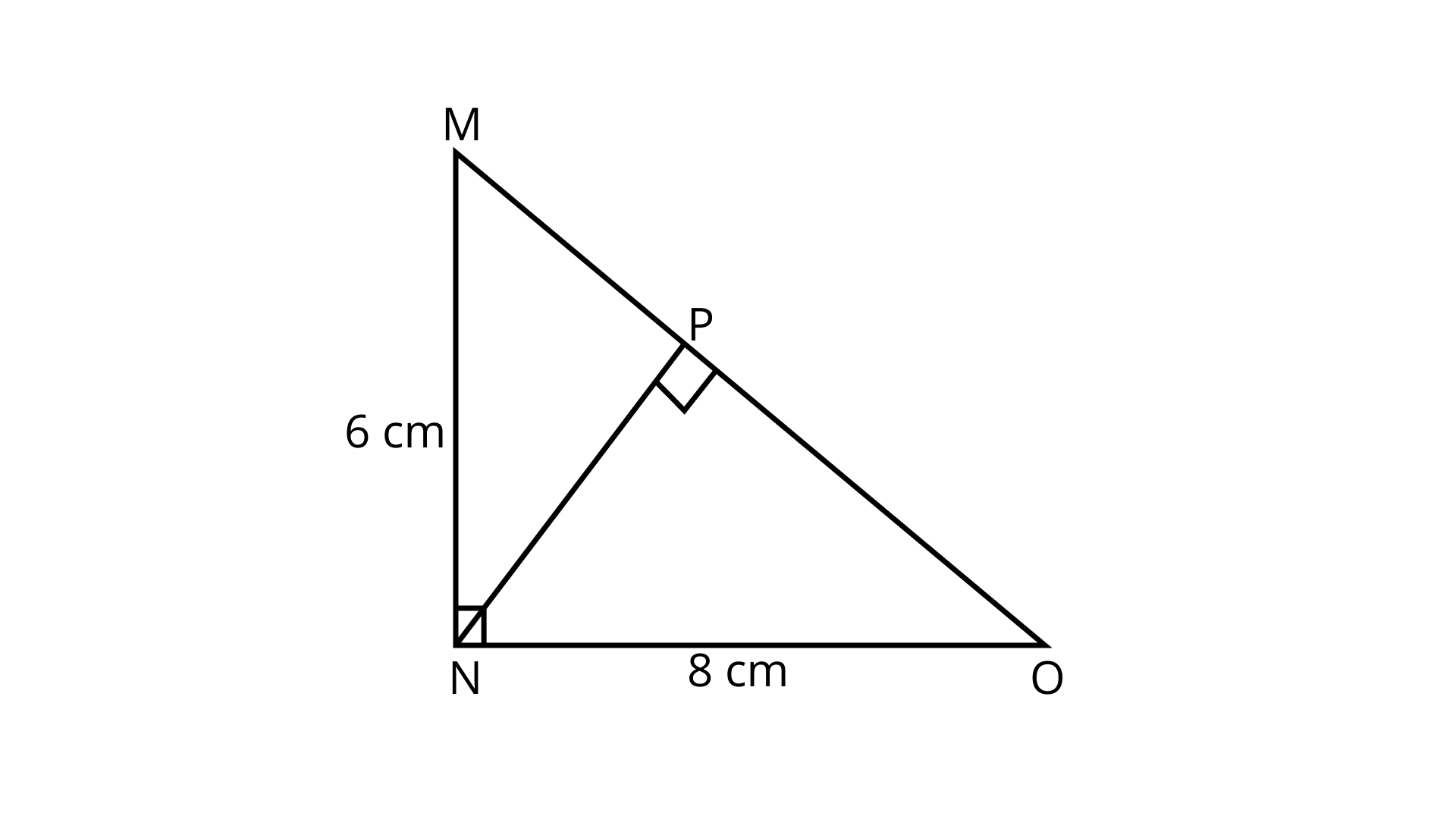
17. In Fig. $9.22$ ${\mathbf{\Delta MNO}}$ is a right-angled triangle. Its legs are ${\mathbf{6\;cm}}$ and ${\mathbf{8\;cm}}$ long. Length of perpendicular \[NP\] on the side \[MO\] is

(a) ${\mathbf{4}}{\mathbf{.8\;cm}}$

(b) ${\mathbf{3}}{\mathbf{.6\;cm}}$

(c) ${\mathbf{2}}{\mathbf{.4\;cm}}$

(d) ${\mathbf{1}}{\mathbf{.2\;cm}}$

Ans: Option (a) is correct.

Given, triangle MNO is a right- angled triangle.

$ \Rightarrow M{O^2} = M{N^2} + N{O^2}$

$ \Rightarrow M{O^2} = {6^2} + {8^2}$

$ \Rightarrow MO = \sqrt {100} $

$ \Rightarrow MO = 10\;{\text{cm}}$

Area of triangle \[MNO\]

$\dfrac{1}{2} \times MN \times NO = \dfrac{1}{2} \times MO \times NP$

$\Rightarrow \dfrac{1}{2} \times 6 \times 8 = \dfrac{1}{2} \times 10 \times NP$

$\Rightarrow NP = \dfrac{{24}}{5}$

$\Rightarrow NP = 4.8\;{\text{cm}}$

18. Area of a right-angled triangle is ${\mathbf{30\;c}}{{\mathbf{m}}^{\mathbf{2}}}$. If its smallest side is ${\mathbf{5\;cm}}$, then its hypotenuse is

(a) ${\mathbf{14\;cm}}$

(b) ${\mathbf{13\;cm}}$

(c) ${\mathbf{12\;cm}}$

(d) ${\mathbf{11\;cm}}$

Ans: Option (b) is correct.

Given, area of right angled triangle $ = 30\;{\text{c}}{{\text{m}}^2}$

Smallest side $ = 5\;{\text{cm}}$

We know that,

Area of triangle ${\text{PQR}} = \dfrac{1}{2} \times $ base $ \times $ height

$\Rightarrow 30 = \dfrac{1}{2} \times 5 \times H$

$\Rightarrow H = \dfrac{{30 \times 2}}{5}$

Height $ = 12\;{\text{cm}}$

According to the Pythagoras theorem,

${({\text{ Hypotenuse }})^2} = {({\text{ Perpendicular }})^2} + {({\text{ Base }})^2}$

$\Rightarrow {({\text{ Hypotenuse }})^2} = 144 + 25$

$\Rightarrow {({\text{Hypotenuse}})^2} = 169$

Hypotenuse $ = 13\;{\text{cm}}$

19. Circumference of a circle of diameter ${\mathbf{5\;cm}}$ is

(a) ${\mathbf{3}}{\mathbf{.14\;cm}}$

(b) ${\mathbf{31}}{\mathbf{.4\;cm}}$

(c) ${\mathbf{15}}{\mathbf{.7\;cm}}$

(d) ${\mathbf{1}}{\mathbf{.57\;cm}}$

Ans: Option (c) is correct.

Given,

Diameter $ = 5\;{\text{cm}}$

Therefore, Radius $ = \dfrac{5}{2}\;{\text{cm}}$

Since, circumference $ = 2\pi r = 2 \times \dfrac{{22}}{7} \times \dfrac{5}{2}$

$ = \dfrac{{110}}{7} = 15.7\;{\text{cm}}$

20. Circumference of a circle disc is ${\mathbf{88\;cm}}$. Its radius is

(a) ${\mathbf{8\;cm}}$

(b) ${\mathbf{11\;cm}}$

(c) ${\mathbf{14\;cm}}$

(d) ${\mathbf{44\;cm}}$

Ans: Option (c) is correct.

Circumference $ = 2\pi r = 88$

$\Rightarrow 88 = 2 \times \dfrac{{22}}{7} \times r$

$\Rightarrow r = \dfrac{{88 \times 7}}{{2 \times 22}}{\text{ }}$

$\Rightarrow r = 14{\text{cm}}$

Hence, $14\;{\text{cm}}$ is the radius.

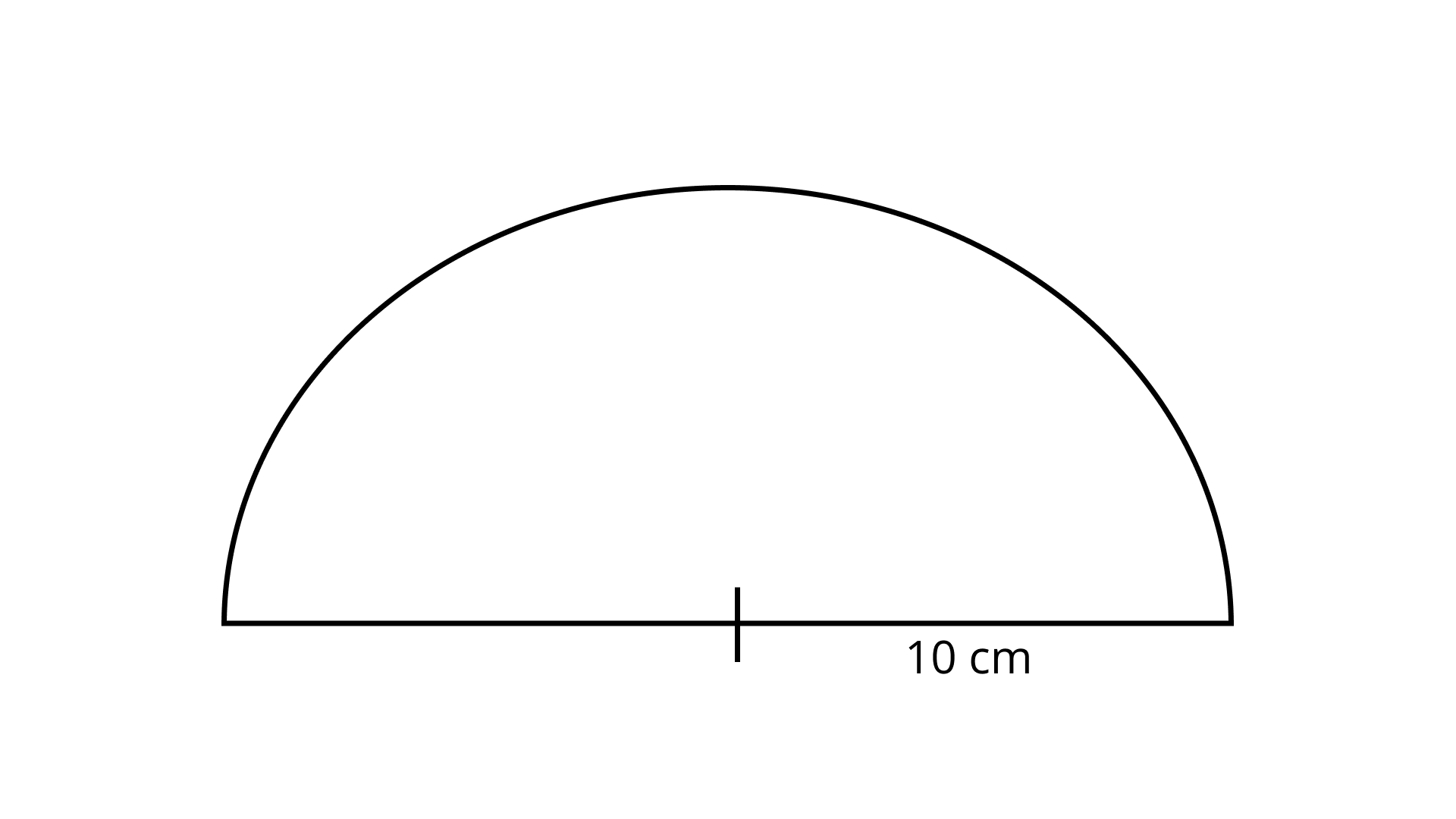
21. Length of tape required to cover the edges of a semicircular disc of radius ${\mathbf{10\;cm}}$ is

(a) ${\mathbf{62}}{\mathbf{.8\;cm}}$

(b) ${\mathbf{51}}{\mathbf{.4\;cm}}$

(c) ${\mathbf{31}}{\mathbf{.4\;cm}}$

(d) ${\mathbf{15}}{\mathbf{.7\;cm}}$

Ans: Option (b) is correct.

Perimeter of the semi-circle $ = $ circumference of semicircle +diameter

circumference of semi-circle $ = \dfrac{{2\pi r}}{2}$

$\dfrac{{22}}{7} \times 10 = 31.4\;{\text{cm}}$

Therefore, total tape required $ = 31.4 + 2 \times 10 = 51.4\;{\text{cm}}$

22. Area of circular garden with diameter ${\mathbf{8\;m}}$ is

(a) ${\mathbf{12}}{\mathbf{.56\;}}{{\mathbf{m}}^{\mathbf{2}}}$

(b) ${\mathbf{25}}{\mathbf{.12\;}}{{\mathbf{m}}^{\mathbf{2}}}$

(c) ${\mathbf{50}}{\mathbf{.24\;}}{{\mathbf{m}}^{\mathbf{2}}}$

(d) ${\mathbf{200}}{\mathbf{.96\;}}{{\mathbf{m}}^{\mathbf{2}}}$

Ans: Option (a) is correct.

Given, diameter is \[8\] metres.

So, radius $ = \dfrac{8}{2}m = 4m$

Hence, area of the circular garden

$ = \pi {r^2} = \dfrac{{22}}{7} \times 4 \times 4$

$ = 50.24{m^2}$

23. Area of a circle with diameter ' ${\mathbf{m}}$ ' radius ' ${\mathbf{n}}$ ' and circumference ' ${\mathbf{p}}$ ' is

(a) ${\mathbf{2\pi n}}$

(b) ${\mathbf{\pi }}{{\mathbf{m}}^{\mathbf{2}}}$

(c) ${\mathbf{\pi }}{\kern 1pt} {\kern 1pt} {\kern 1pt} {{\mathbf{p}}^{\mathbf{2}}}$

(d) ${\mathbf{\pi }}{{\mathbf{n}}^{\mathbf{2}}}$

Ans: Option (d) is correct.

Given,

Diameter $ = {\text{m}}$,

Radius $ = {\text{n}}$,

Circumference $ = {\text{p}}$.

Hence, area of circle $ = \pi {r^2} = \pi {n^2}$

24. A table top is semicircular in shape with diameter ${\mathbf{2}}{\mathbf{.8\;m}}$. Area of this table top is

(a) ${\mathbf{3}}{\mathbf{.08\;}}{{\mathbf{m}}^{\mathbf{2}}}$

(b) ${\mathbf{6}}{\mathbf{.16\;}}{{\mathbf{m}}^{\mathbf{2}}}$

(c) ${\mathbf{12}}{\mathbf{.32\;}}{{\mathbf{m}}^{\mathbf{2}}}$

(d) ${\mathbf{24}}{\mathbf{.64\;}}{{\mathbf{m}}^{\mathbf{2}}}$

Ans: Option (a) is correct.

Given,

Diameter $ = 2.8\;{\text{m}}$,

Radius $ = 1.4\;{\text{m}}$,

Hence,

Area of table top $ = $ area of semicircle

$ = \dfrac{{\pi {r^2}}}{2}$

$ = \dfrac{{22}}{7} \times \dfrac{{1.4}}{2} \times 1.4$

$ = 3.08\;{{\text{m}}^2}$

25. If ${\mathbf{1\;}}{{\mathbf{m}}^{\mathbf{2}}}{\mathbf{ = x\;m}}{{\mathbf{m}}^{\mathbf{2}}}$, then the value of ${\mathbf{x}}$ is

(a) \[{\mathbf{1000}}\]

(b) \[{\mathbf{10000}}\]

(c) \[{\mathbf{100000}}\]

(d) \[{\mathbf{1000000}}\]

Ans: Option (d) is correct.

Given, $1\;{{\text{m}}^2} = x\;{\text{m}}{{\text{m}}^2}$

$\Rightarrow {(1000\;{\text{mm}})^2} = xm{m^2}$

$\Rightarrow x = 1000000$

26. If ${\mathbf{p}}$ squares of each side ${\mathbf{1\;mm}}$ makes a square of side ${\mathbf{1\;cm}}$, then ${\mathbf{p}}$ is equal to

(a) \[{\mathbf{10}}\]

(b) \[{\mathbf{100}}\]

(c) \[{\mathbf{1000}}\]

(d) \[{\mathbf{10000}}\]

Ans: Option (b) is correct.

Since, area of one square having side of $1\;{\text{mm}}$ $ = 1 \times 1\;{\text{m}}{{\text{m}}^2} = 1\;{\text{m}}{{\text{m}}^2}$

Area of the square having side of $1\;{\text{cm}}$

$p \times 1\;{\text{m}}{{\text{m}}^2} = 1\;{\text{c}}{{\text{m}}^2}$

$\Rightarrow p\;{\text{m}}{{\text{m}}^2} = {(10\;{\text{mm}})^2}$

$\Rightarrow p\;{\text{m}}{{\text{m}}^2} = 100\;{\text{m}}{{\text{m}}^2}$

$\Rightarrow p = 100$

27. ${\mathbf{12\;}}{{\mathbf{m}}^{\mathbf{2}}}$ is the area of

(a) a square with side ${\mathbf{12\;m}}$

(b) \[{\mathbf{12}}\] squares with side ${\mathbf{1\;m}}$ each

(c) \[{\mathbf{3}}\] squares with side ${\mathbf{4\;m}}$ each

(d) \[{\mathbf{4}}\] squares with side ${\mathbf{3\;m}}$ each

Ans: Option (b) is correct.

According to the option (b)

\[12\] squares with side $1\;{\text{m}}$ each,

Area of square $ = l \times b = l \times l$

$ \Rightarrow 12 \times 1 \times 1 = 12\;{{\text{m}}^2}$

28. If each side of a rhombus is doubled, how much will its area increase?

(a) ${\mathbf{1}}{\mathbf{.5}}$ times

(b) \[{\mathbf{2}}\] times

(c) \[{\mathbf{3}}\] times

(d) \[{\mathbf{4}}\] times

Ans:  Option c is correct.

Let the side of rhombus be $a$

New side of rhombus $ = 2a$

Area of rhombus $ = {a^2}$

New area of rhombus $ = {(2a)^2} = 4{a^2}$

Hence increase in the area of rhombus $ = 4{a^2} - {a^2} = 3{a^2}$

Hence the increase in the area is 3 times the original area.

29. If the sides of a parallelogram are increased to twice its original lengths, how much will the perimeter of the new parallelogram?

(a) ${\mathbf{1}}{\mathbf{.5}}$ times

(b) \[{\mathbf{2}}\] times

(c) \[{\mathbf{3}}\] times

(d) \[{\mathbf{4}}\] times

Ans: Option (b) is correct.

Let 1 be the length and $b$ be the breadth of a parallelogram.

Then, perimeter $ = 2(l + b)$

If both sides of the parallelogram are doubled, then the breadth and length become 2l and $2b$, respectively.

Now, perimeter $ = 2(2l + 2b) = 2 \times 2(l + b)$

Therefore, the perimeter of the parallelogram will be increased by 2 times.

30. If the radius of a circle is increased to twice its original length, how much will the area of the circle increase?

(a) ${\mathbf{1}}{\mathbf{.4}}$ times

(b) \[{\mathbf{2}}\] times

(c) \[{\mathbf{3}}\] times

(d) \[{\mathbf{4}}\] times.

Ans: Option (d) is correct.

Let $r$ be the radii of a circle.

Then, area of circle $ = \pi {r^2}$

If radii are doubled, then radii become $2{\text{r}}$.

Now, area of circle $ = \pi {(2r)^2} = 4\pi {r^2}$

The area of the circle has increased by 4 times.

31. What will be the area of the largest square that can be cut out of a circle of radius ${\mathbf{10\;cm}}$ ?

(a) ${\mathbf{100\;c}}{{\mathbf{m}}^{\mathbf{2}}}$

(b) ${\mathbf{200\;c}}{{\mathbf{m}}^{\mathbf{2}}}$

(c) ${\mathbf{300\;c}}{{\mathbf{m}}^{\mathbf{2}}}$

(d) ${\mathbf{400\;c}}{{\mathbf{m}}^{\mathbf{2}}}$

Ans: Option (b) is correct.

Given, radius of circle $ = 10\;{\text{cm}}$

The diagonal of the square will be equal to the diameter of the circle.

Now, in right-angled triangle ${\text{DAB}}$,

${(BD)^2} = {(AD)^2} + {(AB)^2}$

$\Rightarrow {(20)^2} = {x^2} + {x^2}{\text{ }}$

$\Rightarrow 2{x^2} = 400$

$\Rightarrow {x^2} = 200$

So, $200\;{\text{c}}{{\text{m}}^2}$ is the area of the largest square.

32. What is the radius of the largest circle that can be cut out of the rectangle measuring ${\mathbf{10\;cm}}$ in length and ${\mathbf{8\;cm}}$ in breadth?

(a) ${\mathbf{4\;cm}}$

(b) ${\mathbf{5\;cm}}$

(c) ${\mathbf{8\;cm}}$

(d) ${\mathbf{10\;cm}}$

Ans: Option (a) is correct

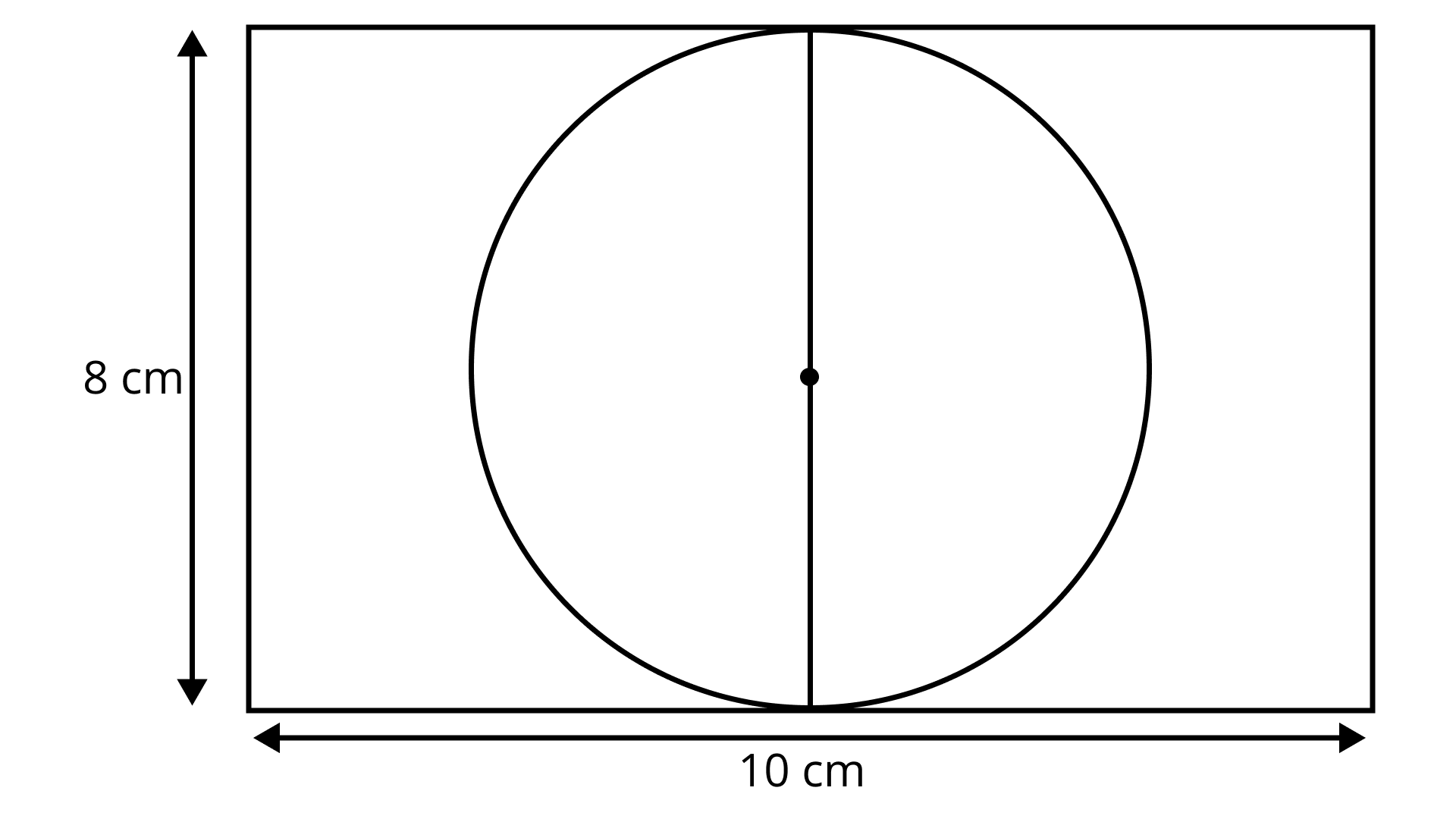
It is clear that the largest circle will have diameter equals the smaller side that is $8\;{\text{cm}}$.

Hence, Radius $ = \dfrac{{{\text{ Diameter }}}}{2} = 4\;{\text{cm}}$

33. The perimeter of the figure ${\mathbf{ABCDEFGHIJ}}$ is

(a) ${\mathbf{60\;cm}}$

(b) ${\mathbf{30\;cm}}$

(c) ${\mathbf{40\;cm}}$

(d) ${\mathbf{50\;cm}}$

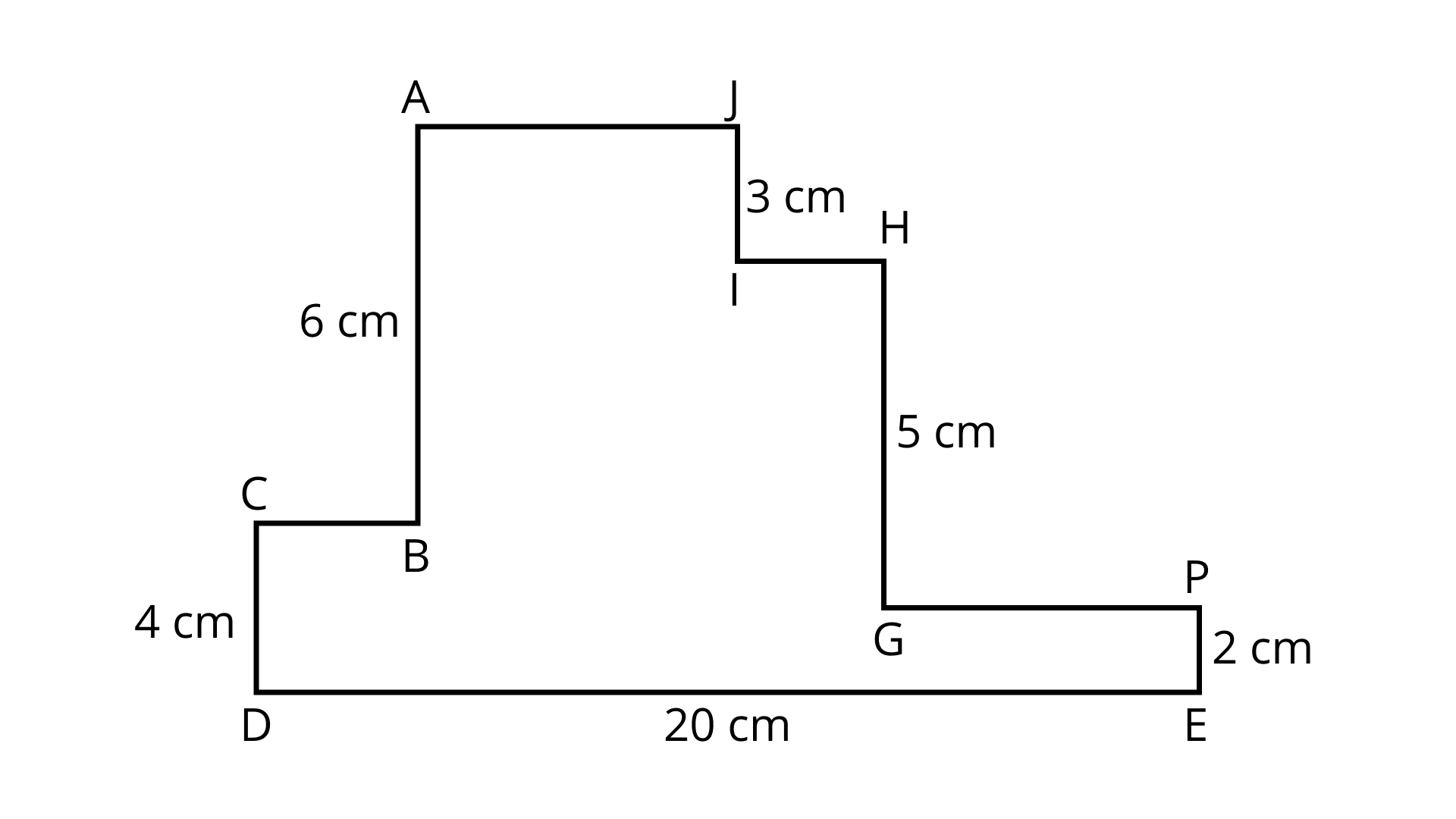
Ans: Option (a) is correct.

Sum of all side \[ = \] Perimeter

$ = AJ + JI + IH + HG + GF + FE + ED + CD + BC + AB$

$ = (AJ + IH + GF + BC) + 3 + 5 + 2 + 20 + 4 + 6$

$ = DE + 40$

$ = 20 + 40 = 60\;{\text{cm}}$

34. The circumference of a circle whose area is ${\mathbf{81\pi }}{{\mathbf{r}}^{\mathbf{2}}}$, is

(a) ${\mathbf{9\pi r}}$

(b) ${\mathbf{18\pi r}}$

(c) ${\mathbf{3\pi r}}$

(d) ${\mathbf{81\pi r}}$

Ans: Option (a) is correct.

Given, area of the circle $ = \pi {R^2} = 81\pi {r^2}$

Hence, radius is ${\text{R}} = 9{\text{r}}$

Circumference of a circle $ = 2\pi R$

Therefore, the circumference of the circle is $ = 18\pi r$

35. The area of a square is ${\mathbf{100\;c}}{{\mathbf{m}}^{\mathbf{2}}}$. The circumference ( in ${\mathbf{cm)}}$ of the largest circle cut of it is

(a) ${\mathbf{5\pi }}$

(b) ${\mathbf{10\pi }}$

(c) ${\mathbf{15\pi }}$

(d) ${\mathbf{20\pi }}$

Ans: Option (a) is correct.

Let a be the side of the square.

Given, area of square $ = 100\;{\text{c}}{{\text{m}}^2}$

$\Rightarrow a = \sqrt {100} $

$\Rightarrow a = 10\;{\text{cm}}$

Now, for the largest circle in the square,

Hence, side of a square $ = $ diameter $ = 10\;{\text{cm}}$ 

$2r = 10\;{\text{cm}}$

$\Rightarrow r = 5\;{\text{cm}}$

Therefore, circumference of the circle

$ = 2\pi r$

$ = 2 \times \pi  \times r$

$ = 10\pi {\text{cm}}$

36. If the radius of a circle is tripled, the area becomes

(a) \[{\mathbf{9}}\] times

(b) \[{\mathbf{3}}\] times

(c) \[{\mathbf{6}}\] times

(d) \[{\mathbf{30}}\] times

Ans: Option (a) is correct.

The area of a circle with radius r is $\pi {r^2}$. 

So, if the radius is tripled, the new radius is 3r

The new area is $\pi {{(3r)}^{2}}$=$9\pi{{r}^{2}}$.

Hence, if the radius of a circle is tripled, the area becomes nine times.

37. The area of a semicircle of radius ${\mathbf{4r}}$ is

(a) ${\mathbf{8\pi }}{{\mathbf{r}}^{\mathbf{2}}}$

(b) ${\mathbf{4\pi }}{{\mathbf{r}}^{\mathbf{2}}}$

(c) ${\mathbf{12\pi }}{{\mathbf{r}}^{\mathbf{2}}}$

(d) ${\mathbf{2\pi }}{{\mathbf{r}}^{\mathbf{2}}}{\mathbf{.}}$

Ans: Option (a) is correct.

Area of semicircle $ = \dfrac{{\pi {r^2}}}{2}$

Then, the area of a semicircle of radius $4r$ is $ = \dfrac{{\left( {\pi {{(4r)}^2}} \right)}}{2}$

$ = \dfrac{{16\pi {r^2}}}{2}$

$ = 8\pi {r^2}$

In Questions 38 To 56, Fill in the Blanks to Make the Statements True.

38. Perimeter of a regular polygon $ = $ length of one side $ \times $_____

Ans: Perimeter of a regular polygon $ = $ length of one side $ \times $ Number of sides.

39. If a wire in the shape of a square is rebent into a rectangle, then the_____of both shapes remain same, but_____ may vary.

Ans: If a wire in the shape of a square is rebent into a rectangle, then the Perimeter of both shapes remain same, but area may vary.

40. Area of the square MNOP of Fig. 9.24 is ${\mathbf{144\;c}}{{\mathbf{m}}^{\mathbf{2}}}$. Area of each triangle is___

Ans: Given, Area of the square MNOP is $144\;{\text{c}}{{\text{m}}^2}$ 

There are 8 triangles in the given squares MNOP 

Hence, area of each triangle $ = \dfrac{1}{8} \times $ Area of square $\operatorname{MNOP} $

$ = \dfrac{1}{8} \times 144 = 18\;{\text{c}}{{\text{m}}^2}$

Area of each triangle is $18{\text{c}}{{\text{m}}^2}$

41. In Fig. 9.25, area of parallelogram BCEF is ___ ${\mathbf{c}}{{\mathbf{m}}^{\mathbf{2}}}$ where ${\mathbf{ACDF}}$ is a rectangle.

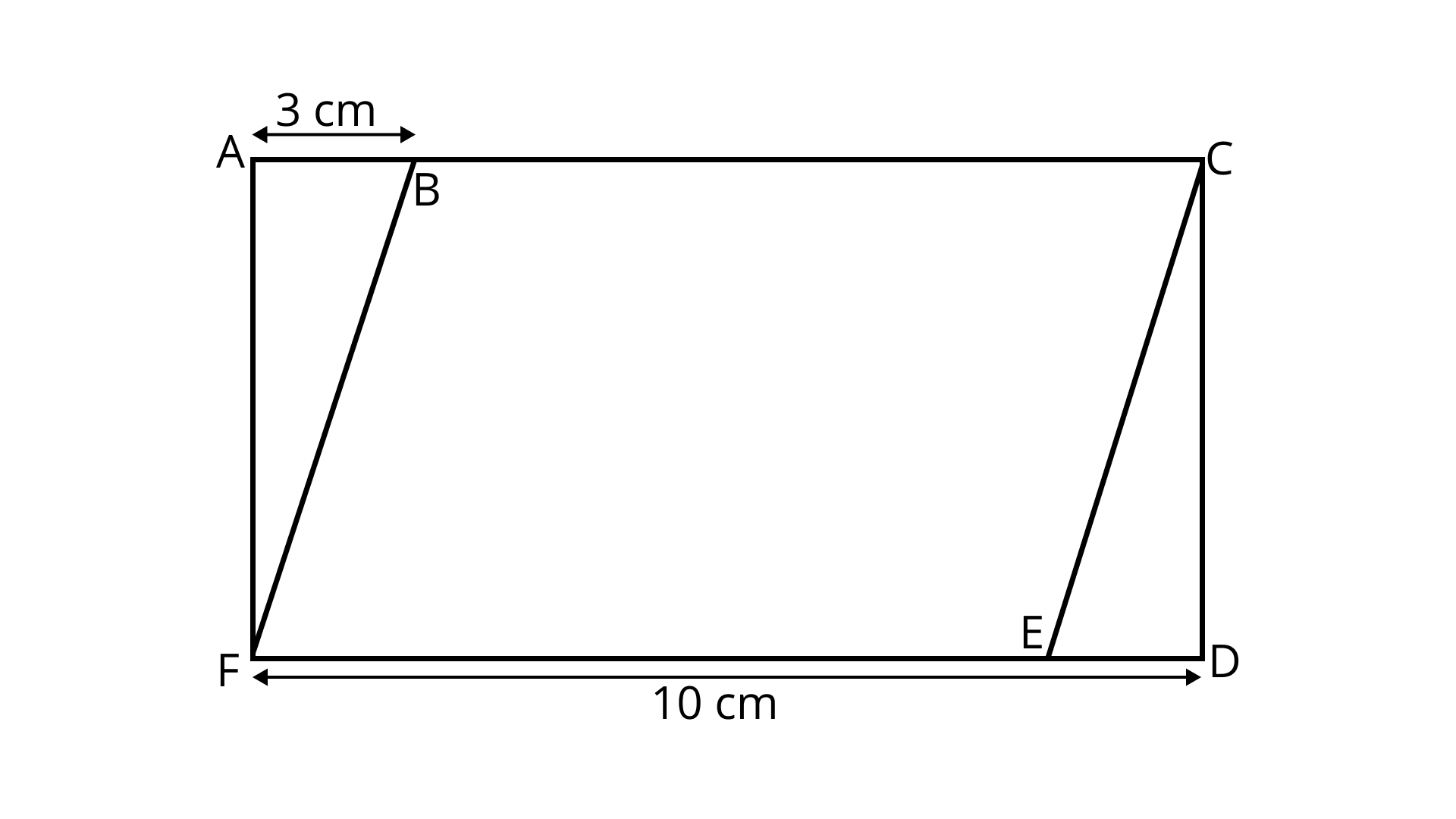
Ans: Area of parallelogram ${\text{BCEF}} = $ Area of rectangle ${\text{ACDF}}$ - Area of triangle ${\text{ABF}}$ - Area of triangle ${\text{CDE}}$

$ = 10 \times 5 - 2 \times \left( {\dfrac{1}{2} \times 3 \times 5} \right)$

$ = 50 - 15$

$ = 35\;{\text{c}}{{\text{m}}^2}$

Area of parallelogram BCEF is $35\;{\text{c}}{{\text{m}}^2}$.

42. To find an area, any side of a parallelogram can be chosen as____ of the parallelogram.

Ans: To find an area, any side of a parallelogram can be chosen as Base of the parallelogram.

43. Perpendicular dropped on the base of a parallelogram from the opposite vertex is known as the corresponding____ of the base.

Ans: Perpendicular dropped on the base of a parallelogram from the opposite vertex is known as the corresponding Height of the base.

44. The distance around a circle is its___

Ans: The distance around a circle is its Circumference

45. Ratio of the circumference of a circle to its diameter is denoted by symbol___

Ans: Circumference $ = 2\pi r$

$C = \pi d{\text{ }}$

$\Rightarrow \dfrac{C}{d} = \pi $

Ratio of the circumference of a circle to its diameter is denoted by symbol $\pi $

46. If area of a triangular piece of cardboard is ${\mathbf{90\;c}}{{\mathbf{m}}^{\mathbf{2}}}$, then the length of altitude corresponding to ${\mathbf{20\;cm}}$ long base is ___${\mathbf{cm}}$.

Ans: Area of triangle $ = \dfrac{1}{2} \times $ base $ \times $ height

$90 = \dfrac{1}{2} \times 20 \times h{\text{ }}$

$\Rightarrow h = 9{\text{ cm}}$

If the area of a triangular piece of cardboard is $90\;c{m^2}$, then the length of altitude corresponding to a $20\;cm$ long base is $9cm$.

47. Value of ${\mathbf{\pi }}$ is____ approximately.

Ans: $\pi  = \dfrac{{22}}{7} = 3.14$

Value of ${\mathbf{\pi }}$ is $3.14$ approximately.

48. Circumference ' ${\mathbf{C}}$ ' of a circle can be found by multiplying diameter ' ${\mathbf{d}}$ ' with___

Ans: Circumference $ = 2\pi r$

diameter $ = 2r$

$C = \pi  \times d$

Therefore, $\pi $ is the answer.

Circumference ' ${\mathbf{C}}$ ' of a circle can be found by multiplying diameter ' ${\mathbf{d}}$ ' with $\pi $

49. Circumference ' ${\mathbf{C}}$ ' of a circle is equal to ${\mathbf{2\pi  \times }}$___

Ans: radius\[\left( r \right).\]

Circumference ' ${\mathbf{C}}$ ' of a circle is equal to ${\mathbf{2\pi  \times }}$$\operatorname{r} $

50. ${\mathbf{1\;}}{{\mathbf{m}}^{\mathbf{2}}}{\mathbf{ = \_\_\_\_c}}{{\mathbf{m}}^{\mathbf{2}}}$.

Ans: $1\;{\text{m}} = 100\;{\text{cm}}$

$\Rightarrow 1{m^2} = {(100)^2}{\text{c}}{{\text{m}}^2}$

$\Rightarrow 1{m^2} = {(100)^2}{\text{c}}{{\text{m}}^2}$

$\Rightarrow 1{m^2} = 10000{\text{c}}{{\text{m}}^2}$

51. ${\mathbf{1\;c}}{{\mathbf{m}}^{\mathbf{2}}}{\mathbf{ = \_\_\_\_m}}{{\mathbf{m}}^{\mathbf{2}}}$.

Ans: $1\;{\text{cm}} = 10\;{\text{mm}}$

$\Rightarrow 1\;{\text{c}}{{\text{m}}^2} = {(10)^2}\;{\text{m}}{{\text{m}}^2}$

$\Rightarrow 1\;{\text{c}}{{\text{m}}^2} = 100\;{\text{m}}{{\text{m}}^2}$

52. 1 hectare  ${\mathbf{ = \_\_\_}}{{\mathbf{m}}^{\mathbf{2}}}{\mathbf{.}}$

Ans: 1 hectare $ = 10000\;{{\text{m}}^2}$

53. Area of a triangle ${\mathbf{ = }}\dfrac{{\mathbf{1}}}{{\mathbf{2}}}$ base $ \times $___

Ans: Area of triangle $ = \dfrac{1}{2} \times $ base $ \times $ height

54. ${\mathbf{1\;k}}{{\mathbf{m}}^{\mathbf{2}}}{\mathbf{ = \_\_\_}}{{\mathbf{m}}^{\mathbf{2}}}$.

Ans: $1\;{\text{km}} = 1000\;{\text{m}}$

$\Rightarrow 1\;{\text{k}}{{\text{m}}^2} = {(1000)^2}\;{{\text{m}}^2}$ 

$\Rightarrow 1\;{\text{k}}{{\text{m}}^2} = 1000000\;{{\text{m}}^2}$

55. Area of a square of side ${\mathbf{6\;m}}$ is equal to the area of___ squares of each side ${\mathbf{1\;cm}}$.

Ans: Area of side $6\;{\text{m}}$ square $ = $ area of side $1\;{\text{cm}}$

$\Rightarrow {(6{\text{m}})^2} = x \times {(1{\text{cm}})^2}$

$\Rightarrow {(600{\text{cm}})^2} = x{\text{c}}{{\text{m}}^2}$

$\Rightarrow 360000{\text{c}}{{\text{m}}^2} = x{\text{c}}{{\text{m}}^2}$

$\Rightarrow x = 360000$

56. ${\mathbf{10\;c}}{{\mathbf{m}}^{\mathbf{2}}}{\mathbf{ = \_\_\_}}{{\mathbf{m}}^{\mathbf{2}}}$ 

Ans:  $1\;{\text{cm}} = \dfrac{1}{{100}}\;{\text{m}}$

$\Rightarrow 10{\text{c}}{{\text{m}}^2} = 10 \times {\left( {\dfrac{1}{{10000}}} \right)}{{\text{m}}^2}$

$\Rightarrow 10{\text{c}}{{\text{m}}^2} = 0.001{{\text{m}}^2}$

In Questions 57 to 72, state whether the statements are True or False.

57. In Fig. 9.26, the perimeter of (ii) is greater than that of (i), but its area is smaller than that of (i).

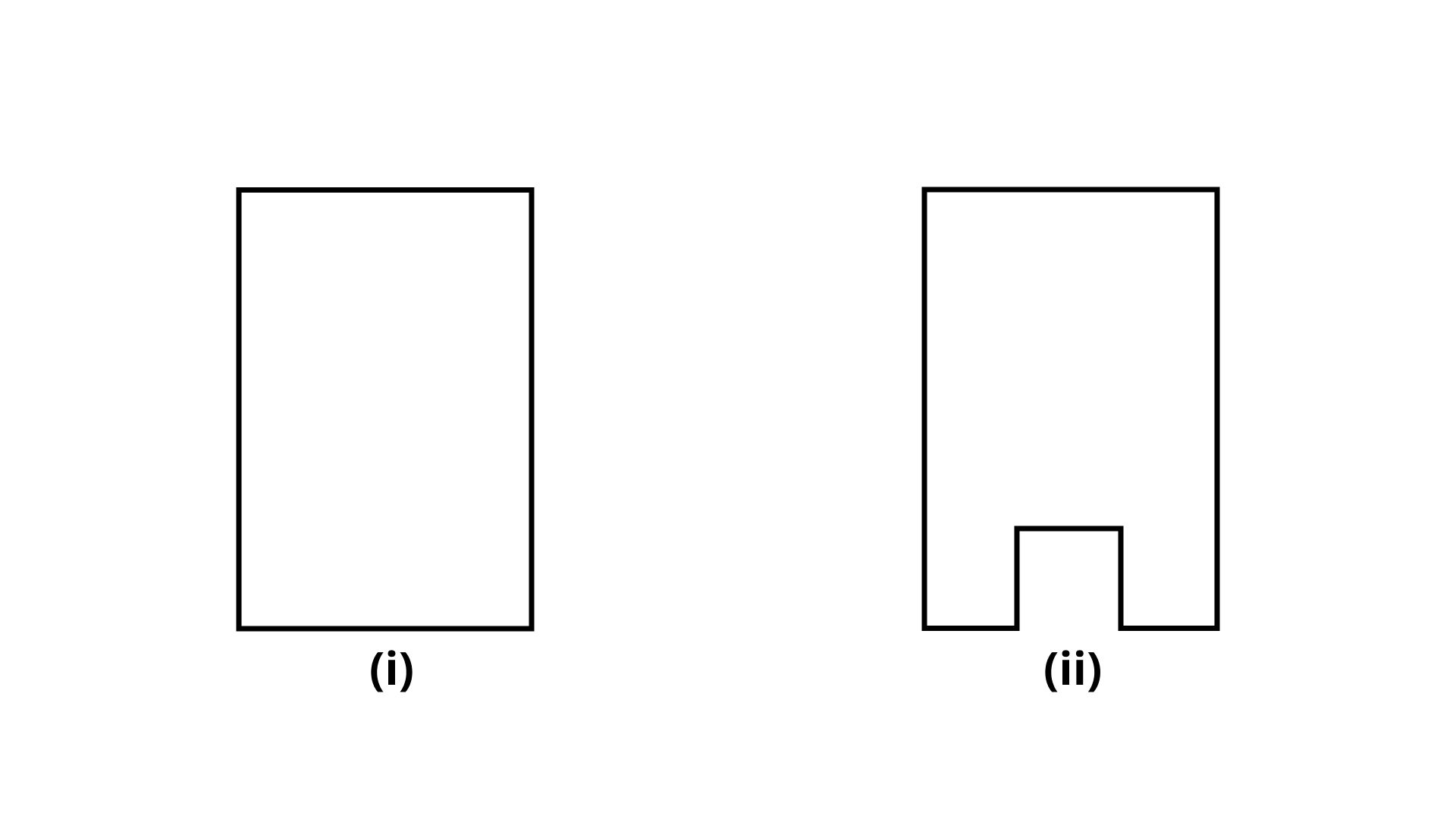
Ans: The statement is True

Perimeter of the figure (ii) is greater than that of figure (i) because some part is being cut and that part has created a dip in the figure. So the perimeter is increased because now we have to add the height of the dip along with the perimeter of the figure (i).

58. In Fig. 9.27,

(a) area of (i) is the same as the area of (ii).

Ans: The statement is True

In the given figure, the numbers of blocks are the same. 

Therefore, the area of both figures is the same.

(b) Perimeter of (ii) is the same as (i).

Ans: The statement is False

Two new sides are added in figure (ii). Hence, the perimeter of figure (ii) is greater than figure (i).

(c) If (ii) is divided into squares of unit length, then its area is \[{\mathbf{13}}\] unit squares.

Ans: The statement is  False

Area of 1 squares $ = 1 \times 1 = 1$ unit squares

Number of squares $ = 12$

Therefore, total area $ = 12 \times 1 = 12$ unit squares

(d) Perimeter of (ii) is \[{\mathbf{18}}\] units.

Ans: The statement is True

So, the perimeter is the sum of all sides. Hence, it is \[18\] units.

59. If the perimeter of two parallelograms are equal, then their areas are also equal.

Ans: The statement is False

Their corresponding height and sides may be different.

So, the area cannot be equal.

60. All congruent triangles are equal in area.

Ans: The statement is True

Congruent triangles have equal size and shape.

Therefore, their areas are also equal.

61. All parallelograms having equal areas have the same perimeters.

Ans: The statement is False

Because it may be possible their height and base can be different, in this case not all parallelograms have equal areas.

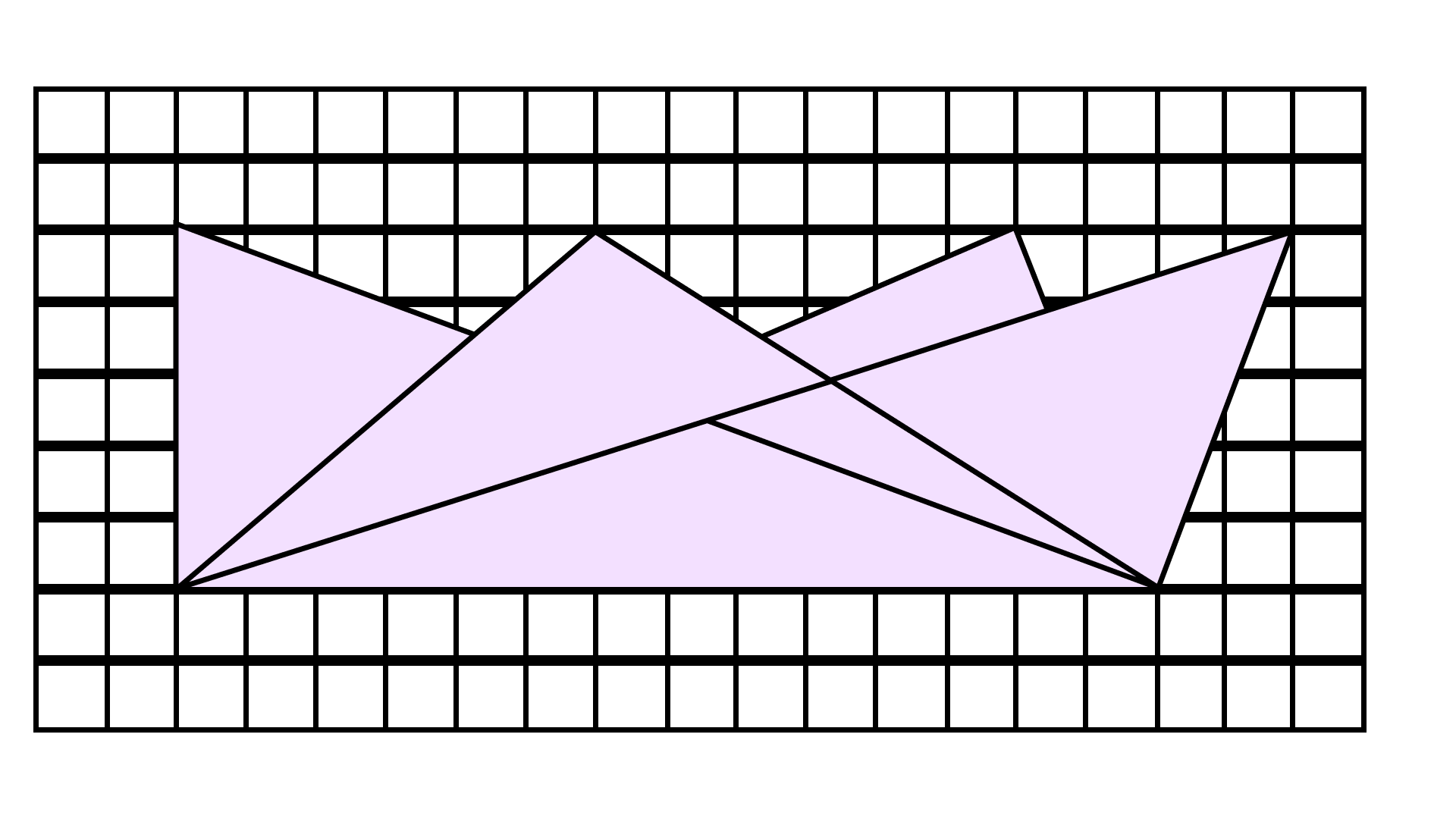
Observe all the four triangles \[{\mathbf{FAB}},{\text{ }}{\mathbf{EAB}},{\text{ }}{\mathbf{DAB}}\] and \[{\mathbf{CAB}}\] as shown in Fig. 9.28.

62. All triangles have the same base and the same altitude.

Ans: The statement is True

It is clear from the figure that all triangles have the same base ${\text{AB}}$ and all the vertices lay on the same line, so the distance between vertex and base of triangle are equal.

63. All triangles are congruent.

Ans: The statement is False

In the given figure, all triangles have only the baseline is equal and no such other lines are equal to each other.

64. All triangles are equal in area.

Ans: The statement is True

Because the triangles between, the same parallel lines and the same base are equal in the area.

65. All triangles may not have the same perimeter.

Ans: The statement is True

In the given figure, it is clear that not all triangles may have the same perimeter.

66. In Fig. 9.29 ratio of the area of triangle ${\mathbf{ABC}}$ to the area of triangle ${\mathbf{ACD}}$ is the same as the ratio of base ${\mathbf{BC}}$ of triangle ${\mathbf{ABC}}$ to the base CD of triangle ACD.

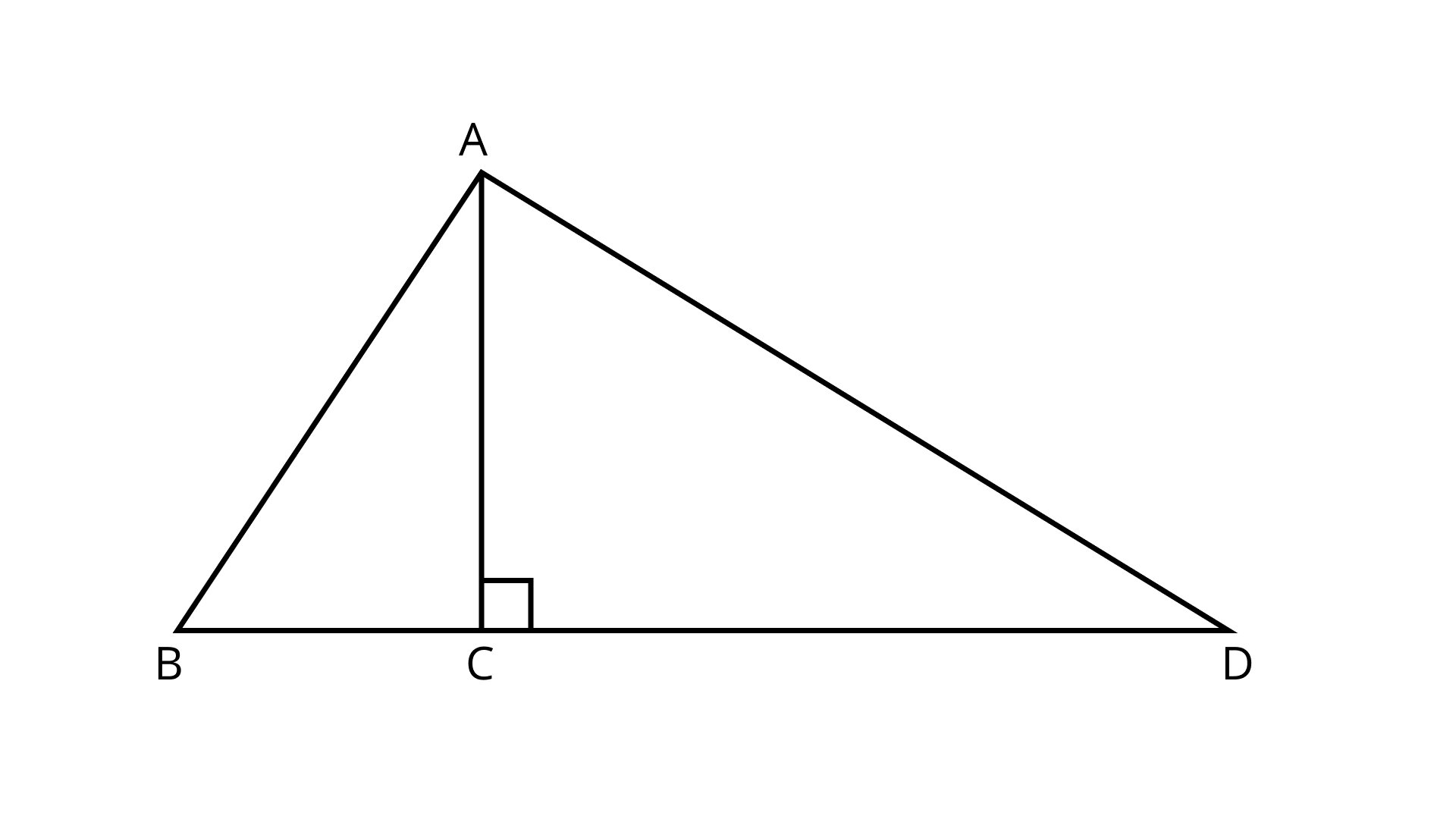
Ans: The statement is True

Area of triangle ${\text{ABC}}$:Area of triangle ${\text{ACD}}$  $= \dfrac{1}{2} \times BC \times AC:\dfrac{1}{2} \times CD \times AC$ 

$ = BC:CD$

67. Triangles having the same base have equal area.

Ans: The statement is False

Area of triangle $ = \dfrac{1}{2} \times $ base $ \times $ height

From the formula, it is clear that the area of triangles depends on base and height not only on the base.

68. Ratio of the circumference of a circle to its radius is always ${\mathbf{2\pi :I}}$.

Ans: The statement is True

Circumference: Radius $ = 2\pi r:{\text{r}} = 2\pi :1$

69. \[{\mathbf{5}}\]hectare $ = {\mathbf{500}}\;{{\mathbf{m}}^{\mathbf{2}}}$

Ans: The statement is False

1 hectare $ = 10000\;{{\text{m}}^2}$

$5 \times 10000\;{{\text{m}}^2} = 50000\;{{\text{m}}^2}$

70. An increase in perimeter of a figure always increases the area of the figure.

Ans: The statement is False

It is not necessary, because the perimeter is the sum of all sides of closed shapes or polygons while the area is just bounded space insides.

71. Two figures can have the same area but different perimeters.

Ans: The statement is True

Yes, because the perimeter is the sum of all sides of closed shapes or polygons while the area is just bounded space insides. Therefore, it can be different.

72. Out of two figures if one has a larger area, then its perimeter need not to be larger than the other figure.

Ans: The statement is True

73. A hedge boundary needs to be planted around a rectangular lawn of size ${\mathbf{72\;m \times 18\;m}}$. If 3 shrubs can be planted in a metre of hedge, how many shrubs will be planted in all?

Ans: Length of rectangular lawn $ = 72$ metres

Breadth of rectangular lawn $ = 18$ metres

Perimeter of rectangle $ = 2$ (Length $ + $ Breadth )

Perimeter of rectangle $ = 2(72 + 18) = 2(90) = 180$ metres

If three shrubs can be planted in a metre of hedge.

Then,

Number of shrubs $ = 3 \times 180 = 540$

74. People of Khejadli village take good care of plants, trees and animals. They say that plants and animals can survive without us, but we can not survive without them. Inspired by her elders Amrita marked some land for her pets (camel and ox) and plants. Find the ratio of the areas kept for animals and plants to the living area.

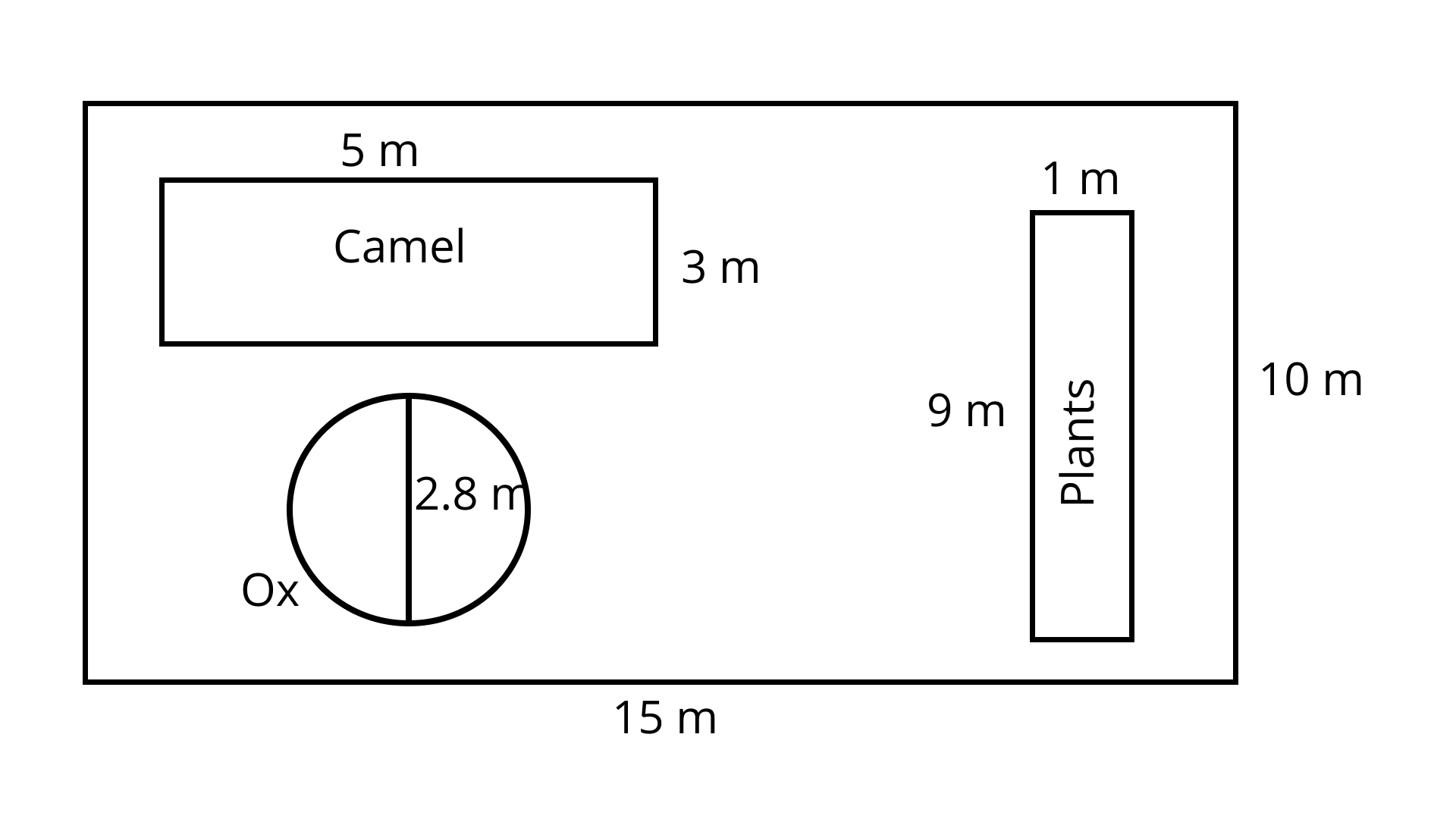
Ans: Area of covered land by plants $ = 9 \times 1 = 9{m^2}$

Area of rectangular land $ = 15 \times 10 = 150\;{{\text{m}}^2}$

Area of covered land by camel $ = 5 \times 3 = 15\;{{\text{m}}^2}$

Hence, the region of land covered by ox in a circular area.

Hence, diameter, ${\text{d}} = 2.8\;{\text{m}}$

Radius $ = 1.4\;{\text{m}}$

Region of land covered by ox

$ = \pi {r^2} = \dfrac{{22}}{7} \times 1.4 \times 1.4 = 6.16\;{{\text{m}}^2}$

Total area covered by Camels, plants and ox $ = 9 + 15 + 6.16 = 30.16\;{{\text{m}}^2}$

So, remaining land $ = 150 - 30.16 = 119.84\;{{\text{m}}^2}$

Ratio of areas kept for animals and plants to the living areas

$30.16:119.84 = 377:1498$

We should save our environment and balance the environment.

75. The perimeter of a rectangle is ${\mathbf{40\;m}}$. Its length is four metres less than five times its breadth. Find the area of the rectangle.

Ans: Let, breadth of rectangle is $x$, then $5x - 4$ be the length of the rectangle.

Perimeter of rectangle $ = 2(l + b)$

$ \Rightarrow 40 = 2(l + b)$

$ \Rightarrow 40 = 2(5x - 4 + x)$

$ \Rightarrow 12x = 40 + 8$

$ \Rightarrow 12x = 48$

$ \Rightarrow x = \dfrac{{48}}{{12}}$

$ \Rightarrow x = 4$

Breadth $ = 4$ metres

Hence, length $ = 5 \times 4 - 4 = 16\;{\text{m}}$

So, area of rectangle $ = 4 \times 16 = 64\;{{\text{m}}^2}$

76. A wall of a room is of dimensions ${\mathbf{5\;m \times 4\;m}}$. It has a window of dimensions ${\mathbf{1}}{\mathbf{.5\;m \times 1\;m}}$ and a door of dimensions ${\mathbf{2}}{\mathbf{.25\;m \times 1\;m}}$. Find the area of the wall which is to be painted.

Ans: Given,

Length of the room $ = 5\;{\text{m}}$

Breadth of the room $ = 4\;{\text{m}}$

Area of the room $ = 5 \times 4 = 20\;{{\text{m}}^2}$

Also,

Length of the window $ = 1.5\;{\text{m}}$ and

Breadth of the window $ = 1\;{\text{m}}$

Area of the window $ = 1.5 \times 1 = 1.5\;{{\text{m}}^2}$

Now,

Length of the door $ = 2.25\;{\text{m}}$

Breadth of the door $ = 1\;{\text{m}}$

Area of the door $ = 2.25 \times 1 = 2.25\;{{\text{m}}^2}$

Now, area of the wall to be painted $ = $ $\text{Area of the room} - (\text{Area of the window} + \text{Area of the door})$

\[ = 20 - \left( {1.5 + 2.25} \right)\]

$ = 20 - 3.75$

$ = 16.25\;{{\text{m}}^2}$

77. Rectangle MNOP is made up of four congruent rectangles (Fig. 9.31). If the area of one of the rectangles is ${\mathbf{8\;}}{{\mathbf{m}}^{\mathbf{2}}}$ and breadth is ${\mathbf{2\;m}}$, then find the perimeter of MNOP.

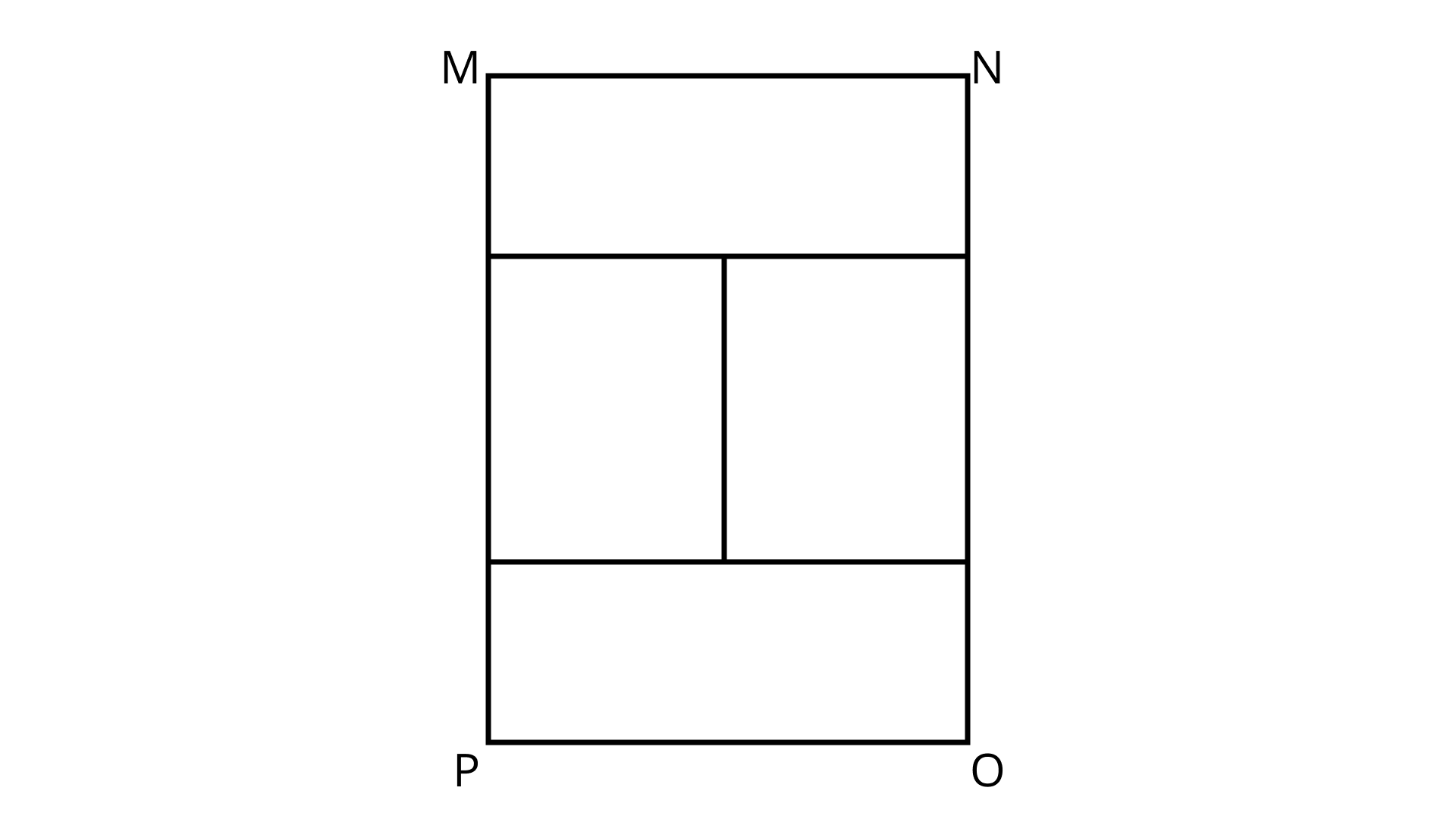
Ans: Given, Area of one rectangle $ = 8{m^2}$

Breadth $ = 2\;{\text{m}}$

$l \times b = 8$

$l \times 2 = 8$

$l = 4m$

Now, perimeter of rectangle MNOP

\[ = MN + NC + CD + DO + PO + PF + FA + MA{\text{ }}\]

\[ = 4 + 2 + 4 + 2 + 4 + 2 + 4 + 2\]

\[ = 24m{\text{ }}\]

So, the perimeter of MNOP is \[24\]metres.

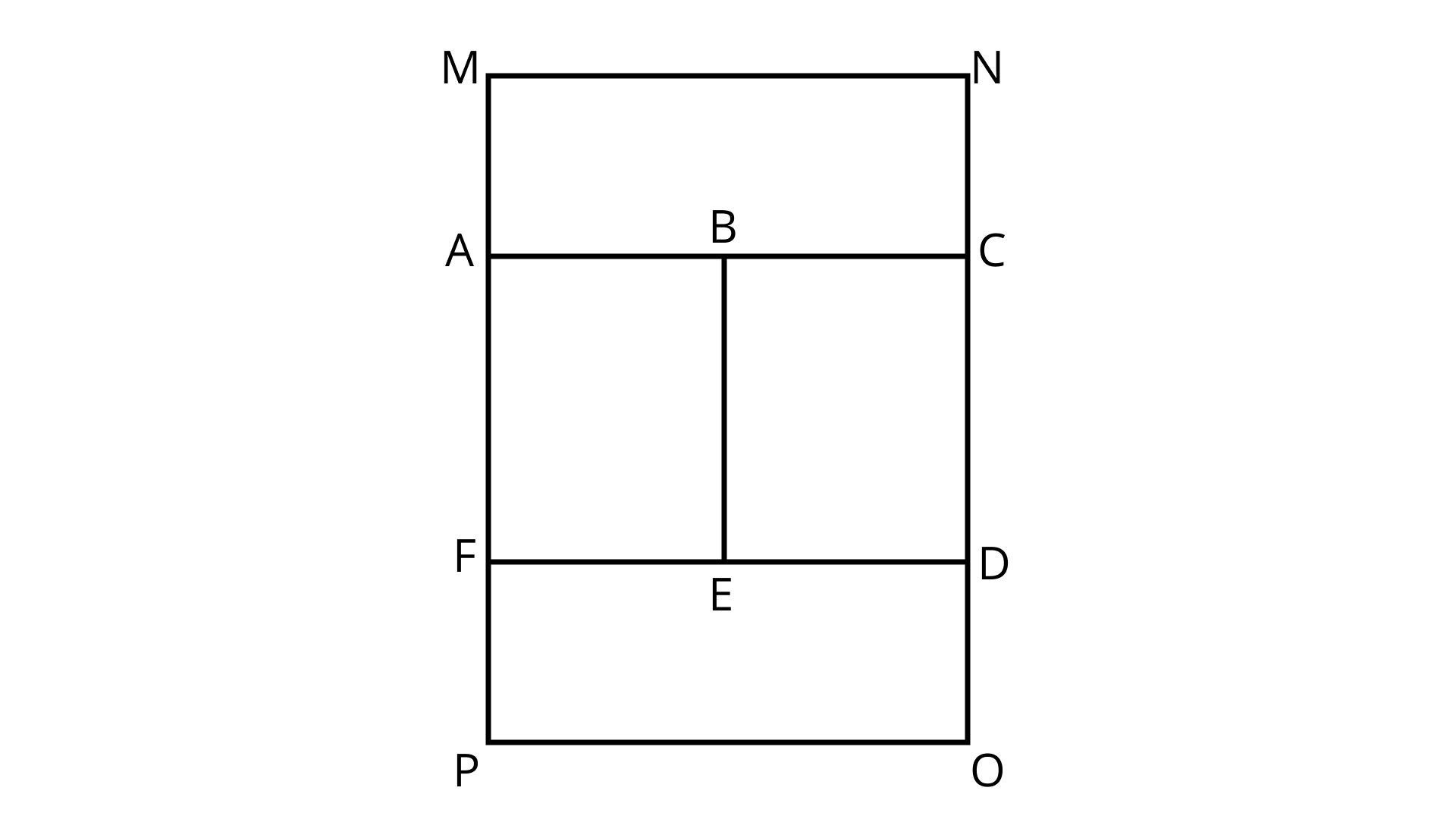
78. In Fig. 9.32, the area of $\vartriangle {\mathbf{AFB}}$ is equal to the area of parallelogram ${\mathbf{ABCD}}$. If altitude ${\mathbf{EF}}$ is ${\mathbf{16\;cm}}$ long, find the altitude of the parallelogram to the base ${\mathbf{AB}}$ of length ${\mathbf{10\;cm}}$. What is the area of $\vartriangle {\mathbf{DAO}}$, where ${\mathbf{O}}$ is the midpoint of DC?

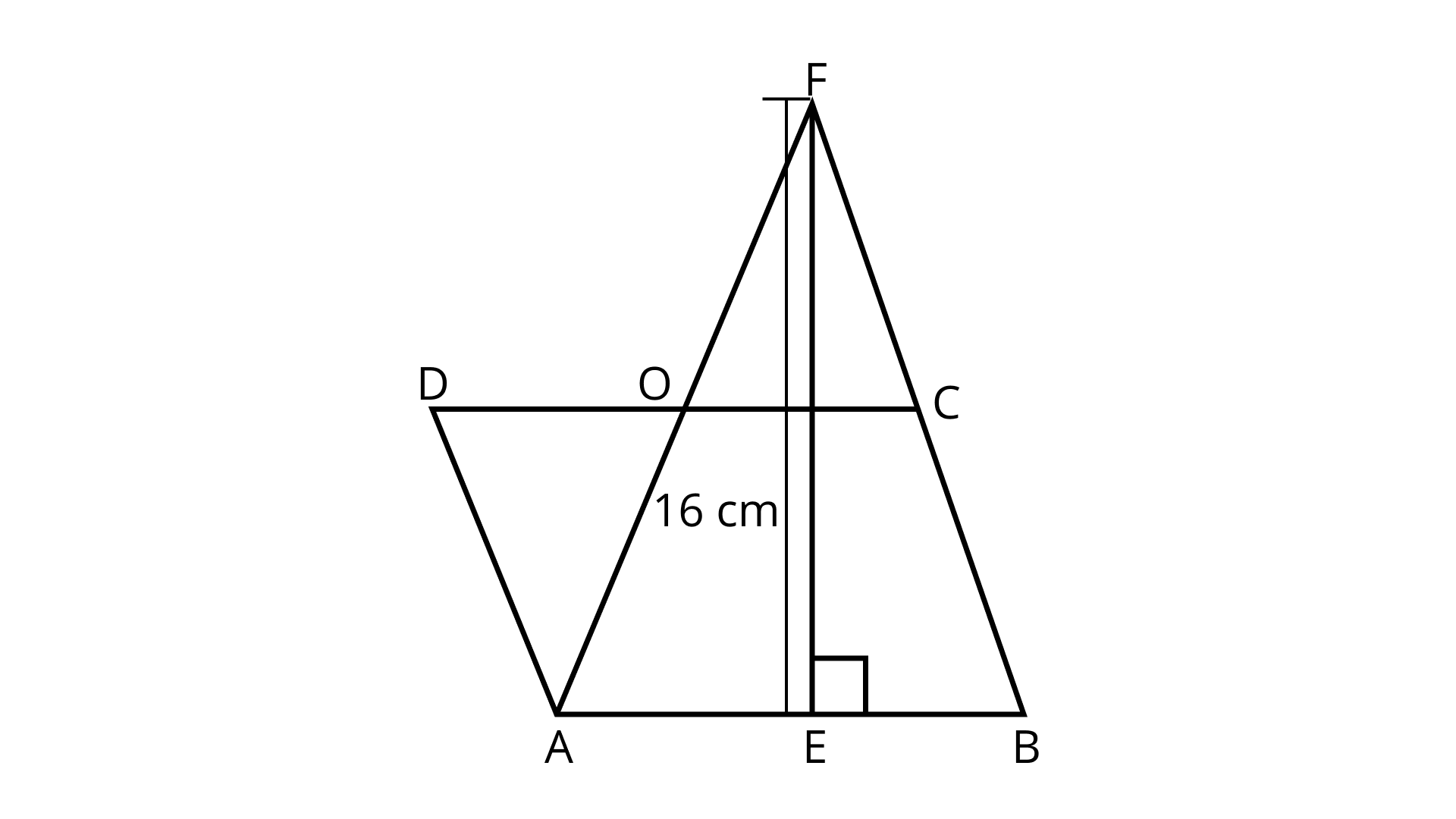
Ans: Given, Area of triangle ${\text{AFB}} = $ Area of parallelogram ABCD

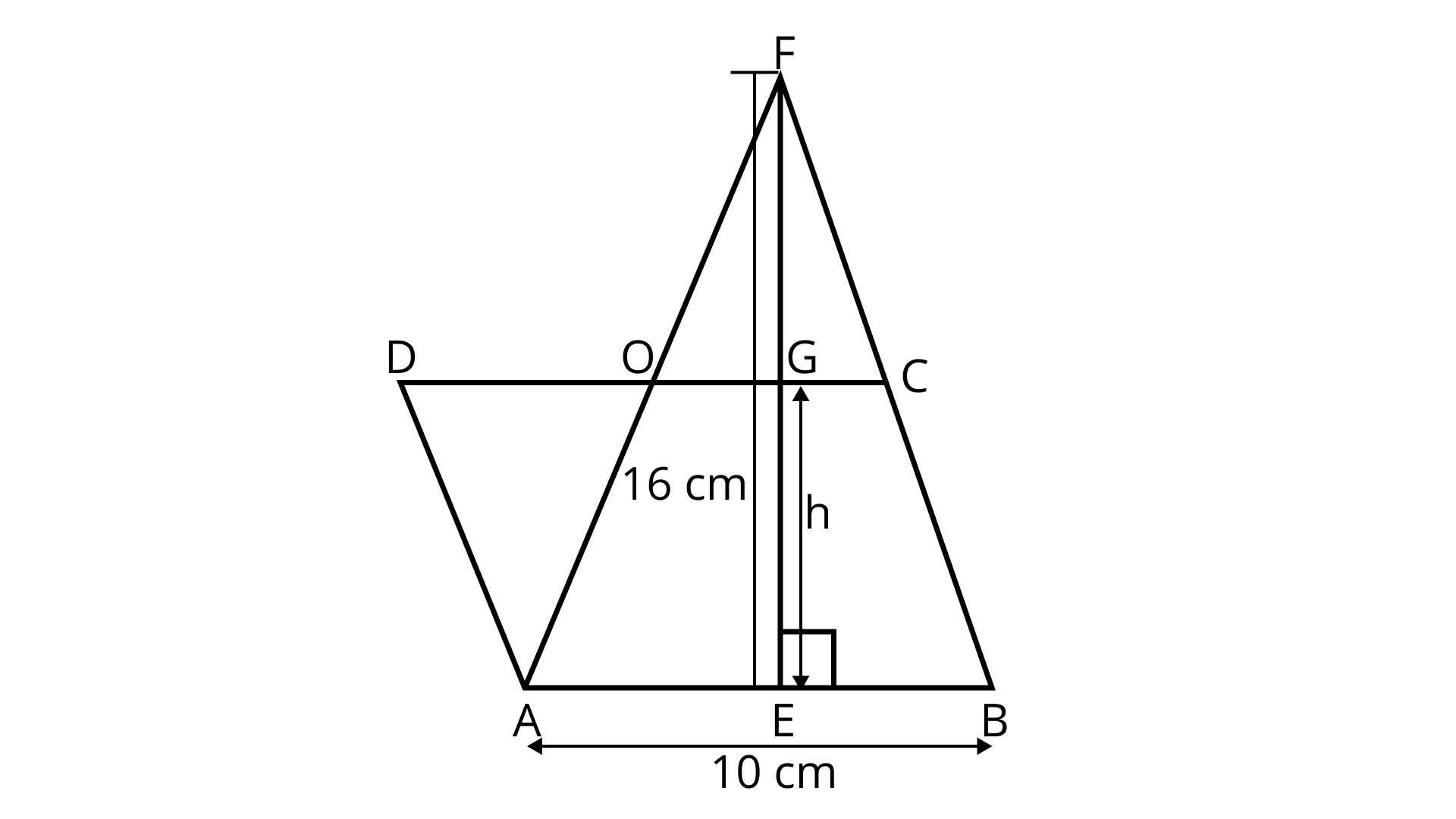
$\dfrac{1}{2} \times AB \times EF = CD \times EG$

Let ${\text{h}}$ be corresponding height

$\dfrac{1}{2} \times 10 \times 16 = 10 \times h$

$\Rightarrow h = 8{\text{cm}}$

In triangle DAO,

DO $ = 5\;{\text{cm}}$

Area of triangle ${\text{DAO}} = \dfrac{1}{2} \times OD \times h$

$ = \dfrac{1}{2} \times 5 \times 8 = 20\;{\text{c}}{{\text{m}}^2}$

79. Ratio of the area of $\Delta {\mathbf{WXY}}$ to the area of $\Delta {\mathbf{WZY}}$ is \[{\mathbf{3:4}}\]${\mathbf{(Fig}}{\mathbf{.9}}{\mathbf{.33)}}{\mathbf{.If}}{\kern 1pt} {\kern 1pt} {\mathbf{the}}{\kern 1pt} {\kern 1pt} {\mathbf{area}}{\kern 1pt} {\kern 1pt} {\mathbf{of}}$$\Delta WXZ$ is ${\mathbf{56\;c}}{{\mathbf{m}}^{\mathbf{2}}}$ and ${\mathbf{WY = 8\;cm}}$, find the lengths of \[XY\]and \[YZ.\]

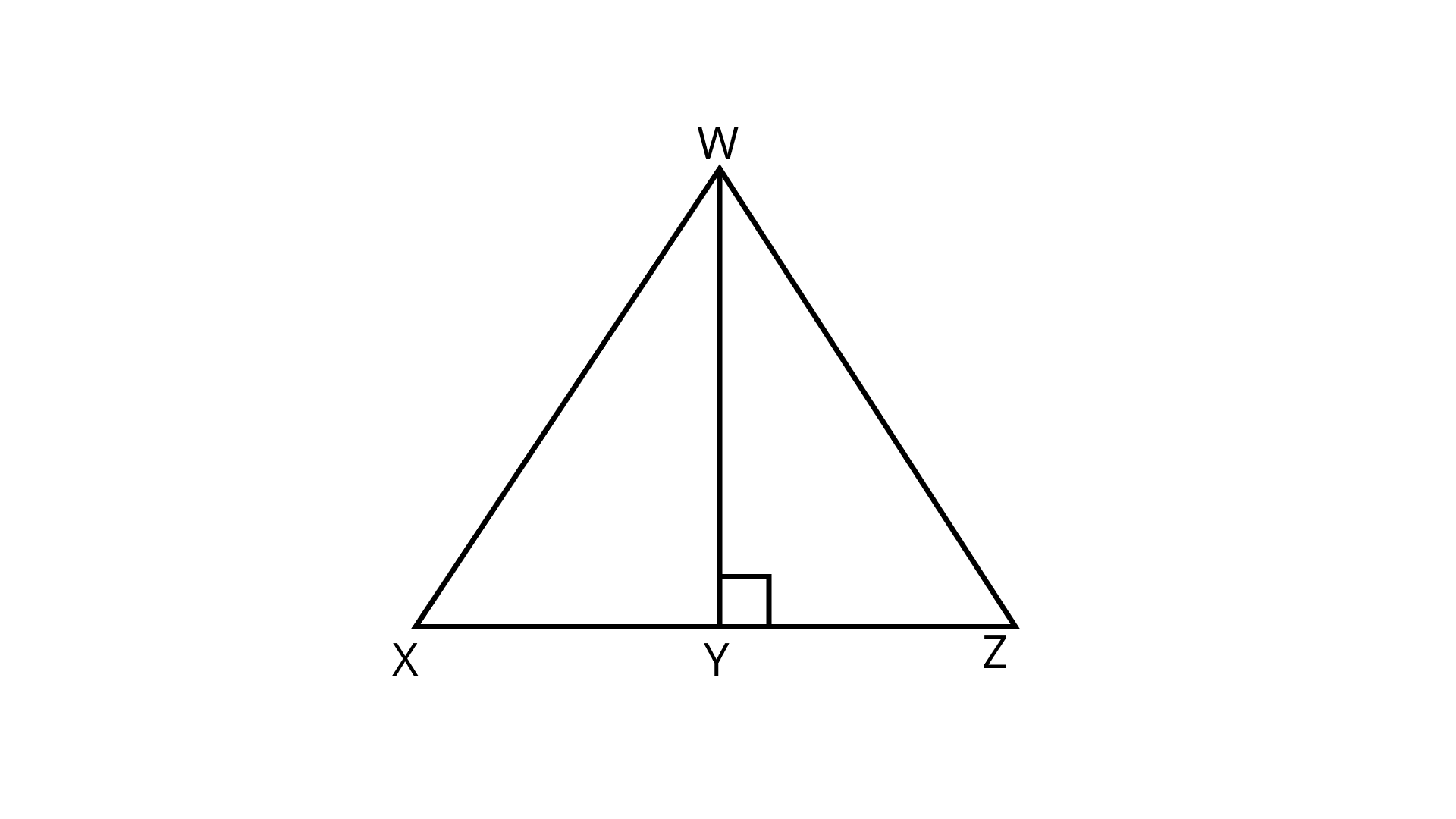
Ans: Area of triangle ${\text{WXZ}} = 56$ sq. ${\text{cm}}$

$\Rightarrow \dfrac{1}{2} \times WY \times XZ = 56$

$\Rightarrow \dfrac{1}{2} \times 8 \times XZ=56$

$\Rightarrow XZ = 14\;{\text{cm}}$

Area of triangle \[WXY:\]Area of triangle \[WZY = 3:4\]

$\dfrac{{\dfrac{1}{2} \times WY \times XY}}{{\dfrac{1}{2} \times YZ \times WY}} = \dfrac{3}{4}$

$\Rightarrow \dfrac{{XY}}{{YZ}} = \dfrac{3}{4}$

$\Rightarrow \dfrac{{XY}}{{14 - XY}} = \dfrac{3}{4}$

$\Rightarrow 4XY = 42 - 3XY$

$\Rightarrow XY = 6\;{\text{cm}}$

Hence, $YZ = XZ - XY = 14 - 6$

$YZ = 8\;{\text{cm}}$

Hence, $XZ = 8$ and $XY = 6\;{\text{cm}}$

80. Rani bought a new field that is next to one she already owns (Fig. 9.34). This field is in the shape of a square of side ${\mathbf{70\;m}}$. She makes a semi-circular lawn of maximum area in this field.

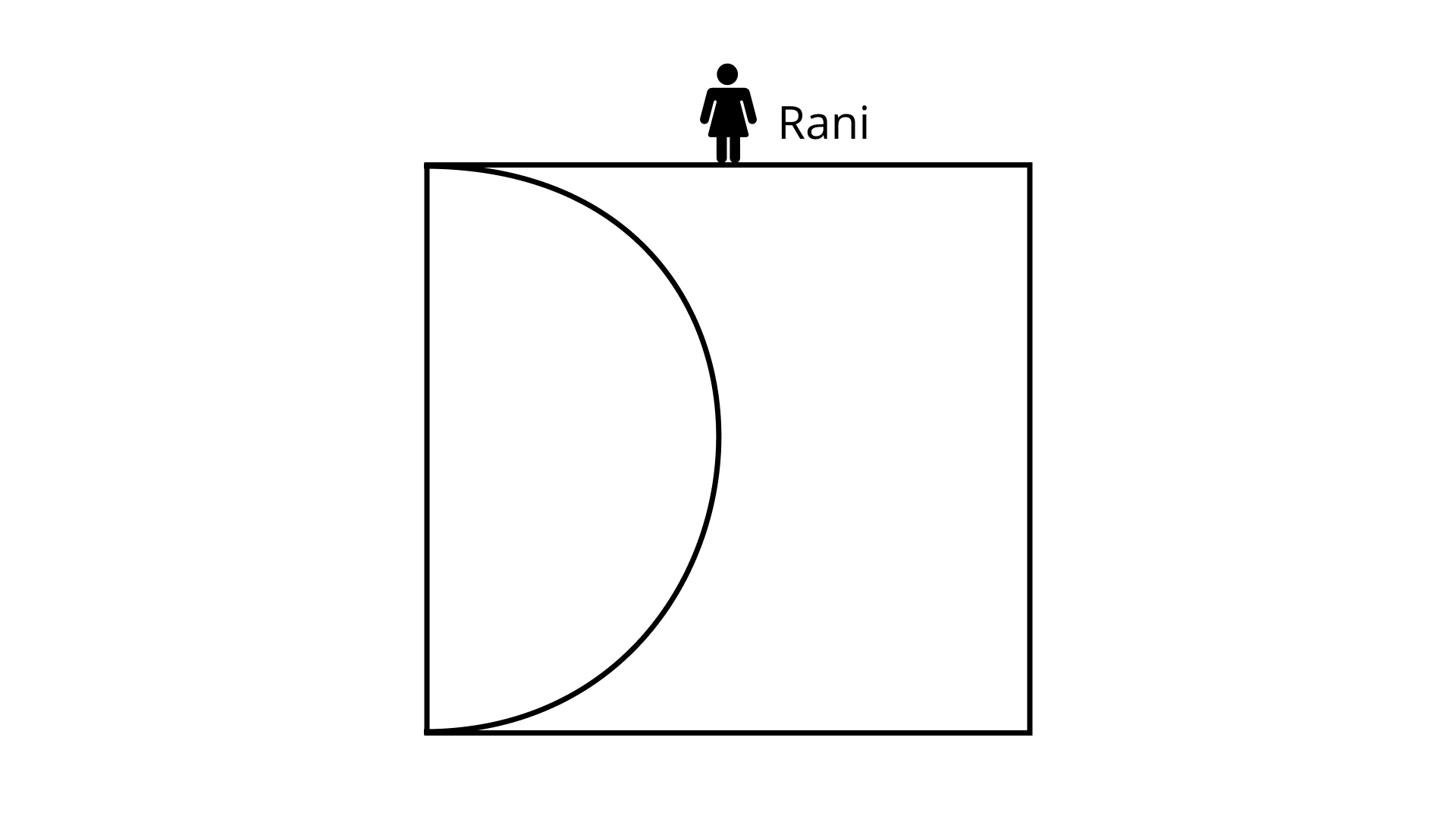
(i) Find the perimeter of the lawn.

Ans: Given,

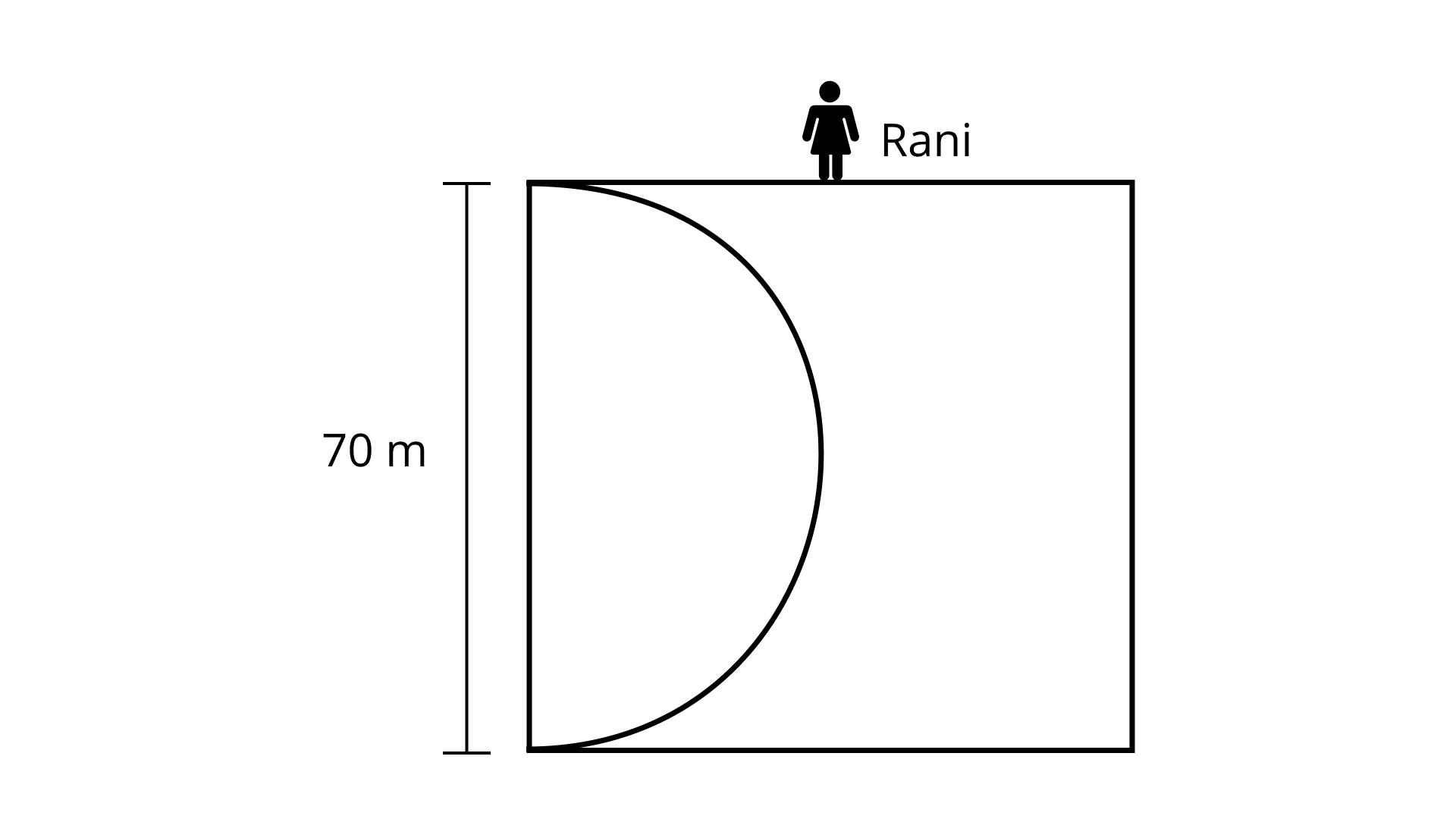
Side of a square field $ = 70\;{\text{m}}$

So, diameter of semi circular lawn = Side of square field $ = 70\;{\text{m}}$

Radius of semi circular lawn $ = \dfrac{{70}}{2} = 35\;{\text{m}}$.

Perimeter of semi circular lawn $ = \pi r + 2r = \dfrac{{22}}{7} \times 35 + 2 \times 35$

$ = 110 + 70 = 180\;{\text{m}}.$

Hence, perimeter of the lawn $180m$

(ii) Find the area of the square field excluding the lawn.

Ans: Area of square $= 70 \times 70 = 4900\;{\text{c}}{{\text{m}}^2}$

Hence, required area

$ = 4900 - \dfrac{1}{2} \times \pi  \times {(35)^2}$

$ = 4900 - 1925$

$ = 2975{m^2}$

81. In Fig. 9.35, find the area of parallelogram ${\mathbf{ABCD}}$ if the area of shaded triangle is ${\mathbf{9\;c}}{{\mathbf{m}}^{\mathbf{2}}}$.

Ans: Given,

Area of shaded portion $ = 9{\text{sq}}.{\text{cm}}$

Base of triangle $ = 3\;{\text{cm}}$

Now, area of triangle,

$9 = \dfrac{1}{2} \times 3 \times h$

$\Rightarrow h = \dfrac{{18}}{3}$

$\Rightarrow h = 6\;{\text{cm}}$

Area of parallelogram $ = 6 \times (3 + 4) = 6 \times 7 = 42\;{\text{c}}{{\text{m}}^2}$

82. Pizza factory has come out with two kinds of pizzas. A square pizza of side $45\;{\text{cm}}$ costs ₹ \[{\mathbf{150}}\] and a circular pizza of diameter ${\mathbf{50\;cm}}$ costs ₹\[{\mathbf{160}}\] (Fig. 9.36). Which pizza is a better deal?

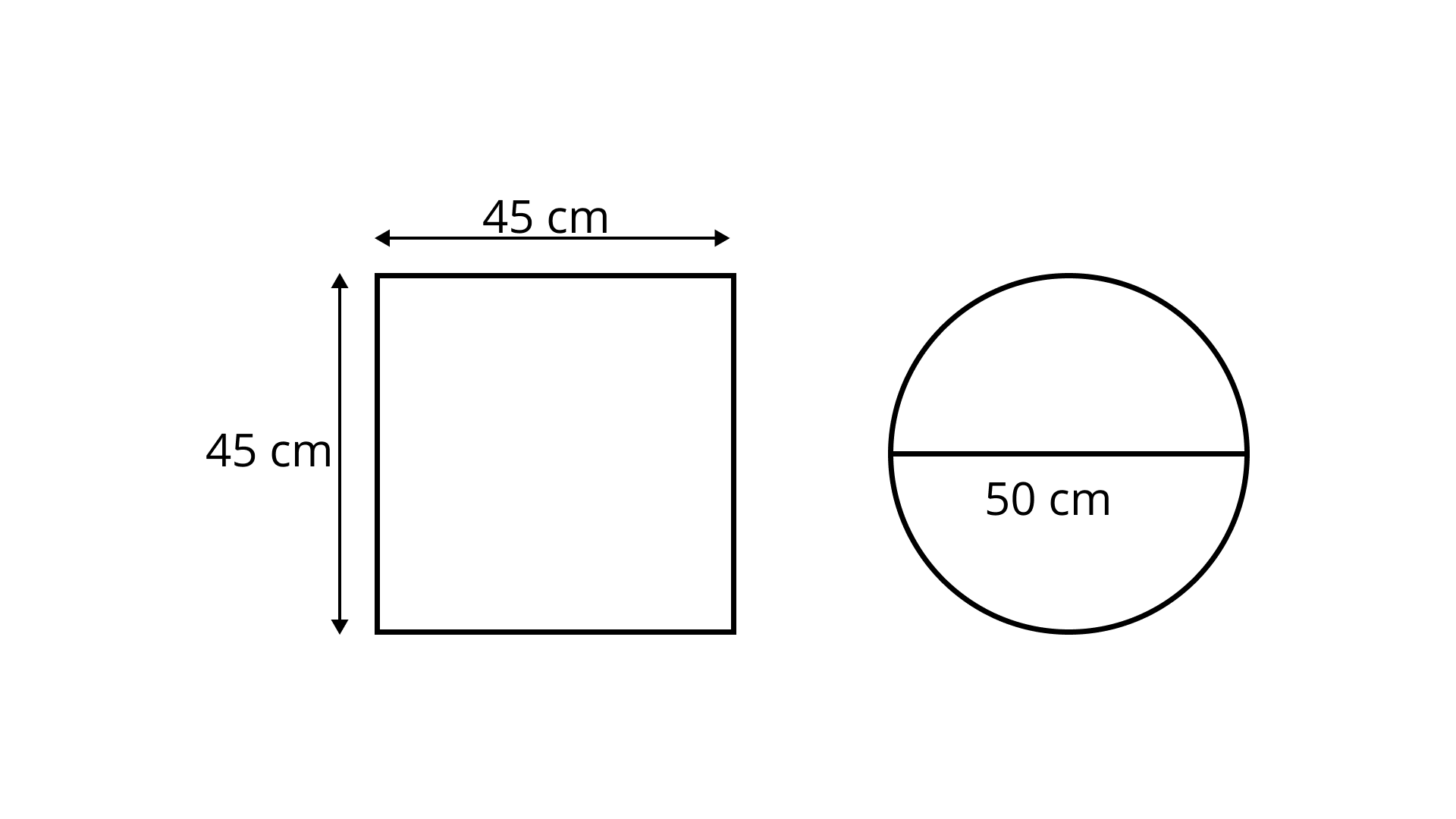
Ans: Given,

Side of square pizza $ = 45\;{\text{cm}}$

Diameter of circular pizza $ = 50\;{\text{cm}}$

Radius $ = 25\;{\text{cm}}$

Area of square pizza $ = 45 \times 45 = 2025\;{\text{c}}{{\text{m}}^2}$

Area of circular pizza $ = \dfrac{{22}}{7} \times 25 \times 25$

$ = \dfrac{{13750}}{7}$ 

$ = 1964.28\;{\text{c}}{{\text{m}}^2}$

$ = 1964.28\;{\text{c}}{{\text{m}}^2}$ 

Therefore, price of $1\;{\text{cm}}$ square pizza

 $ = \dfrac{{2052}}{{150}} = Rs.13.5$

Price of $1\;{\text{cm}}$ circular pizza $ = \dfrac{{1964.28}}{{160}} = Rs.12.27$

Hence, the best deal is circular pizza.

83. Three squares are attached to each other as shown in Fig. 9.37. Each square is attached at the midpoint of the side of the square to its right. Find the perimeter of the complete figure.

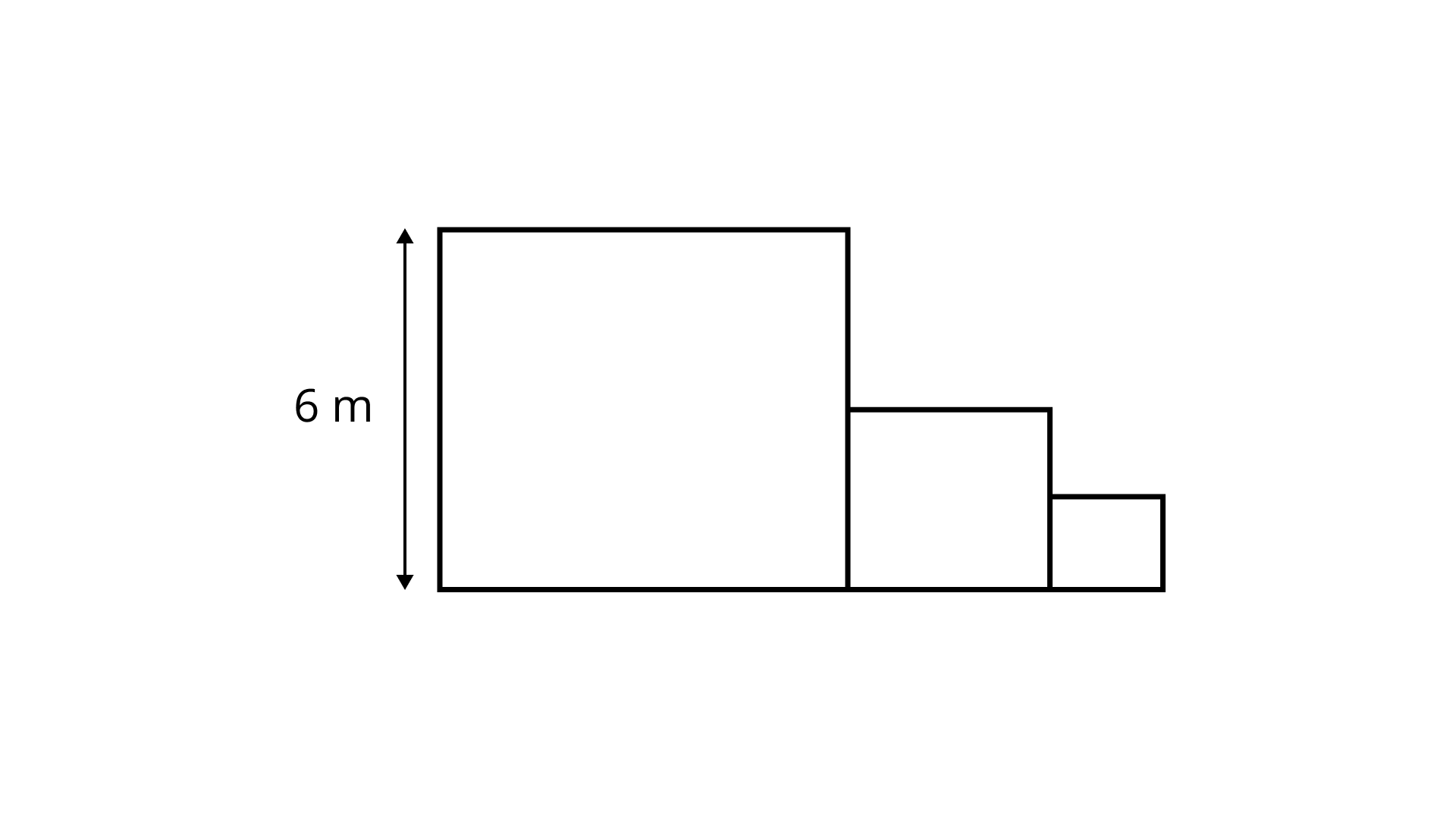
Ans: Perimeter of the complete figure

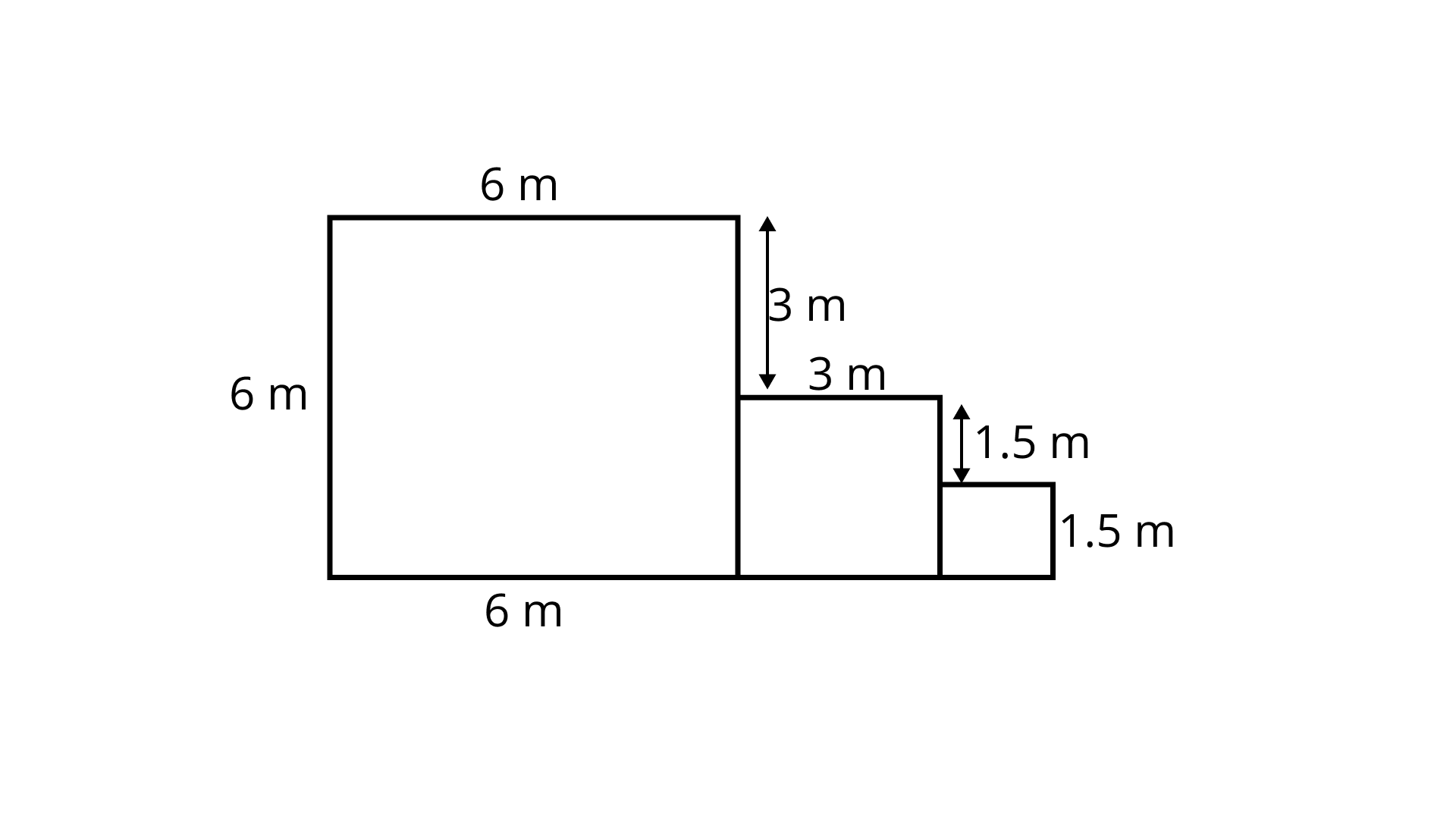
$ = 6 + 6 + 6 + 3 + 1.5 + 1.5 + 1.5 + 3 + 3 + 1.5$

$ = 33{\text{m }}$

84. In Fig. 9.38, ${\mathbf{ABCD}}$ is a square with ${\mathbf{AB = 15\;cm}}$. Find the area of the square\[{\mathbf{BDFE}}\].

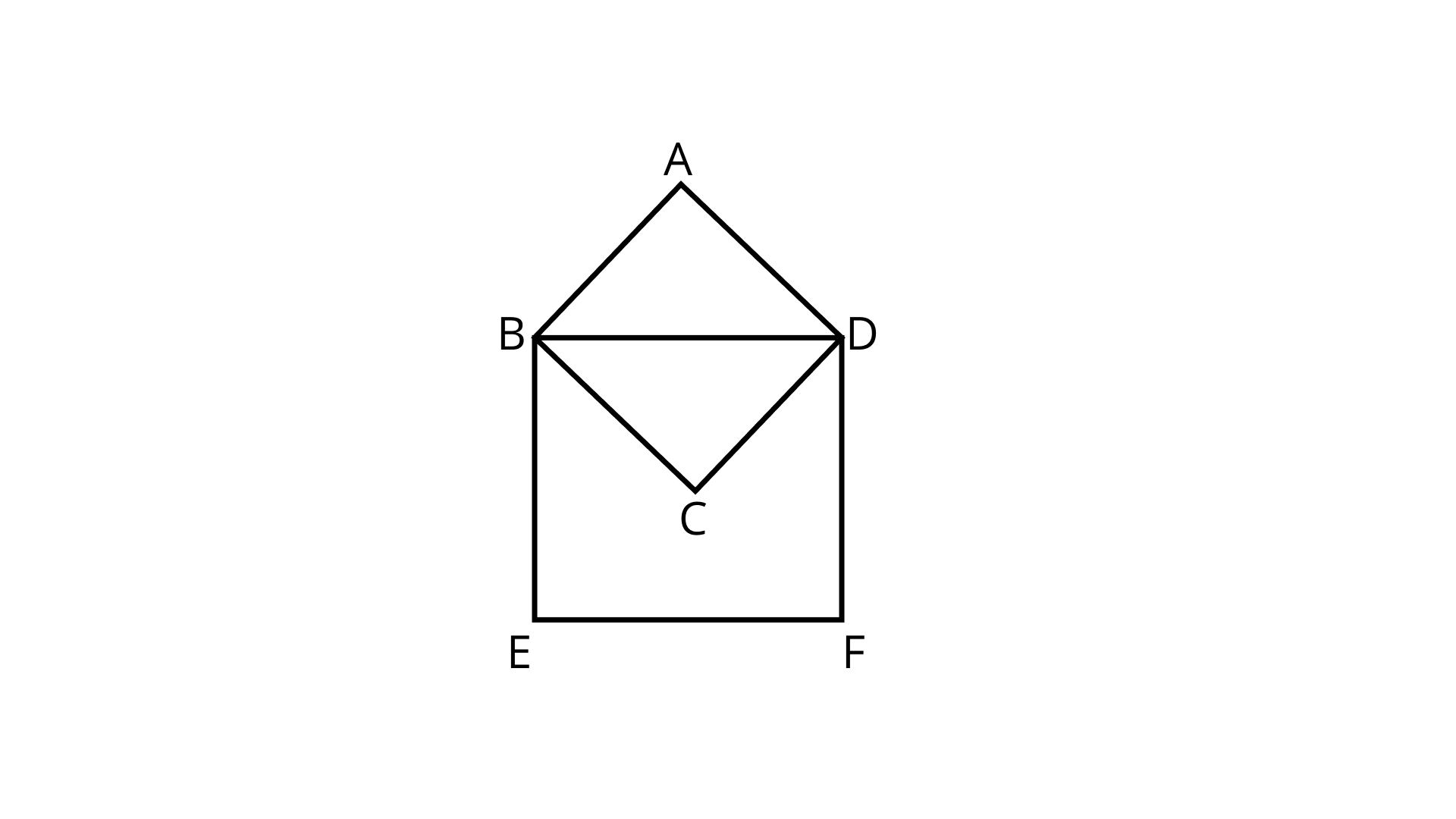
Ans: Given,

${\text{AB}} = 15\;{\text{cm}}$

Diagonal of square $ABCD = 2\sqrt a  = \sqrt 2  \times 15$

$ = 15\sqrt 2 $

From the figure,

Diagonal of square ${\text{ABCD}}$ is the side of square \[\operatorname{BDEF} \]

Therefore, area of the square\[\operatorname{BDEF} \],

$ = {(15\sqrt 2 )^2}$

$ = 15 \times 15 \times \sqrt 2  \times \sqrt 2 $

$ = 225 \times 2$

$ = 450\;{\text{c}}{{\text{m}}^2}$

85. In the given triangles of Fig. 9.39, perimeter of \[\Delta {\mathbf{ABC}} = \]perimeter of $\Delta {\mathbf{PQR}}$. Find the area of $\vartriangle {\mathbf{ABC}}$.

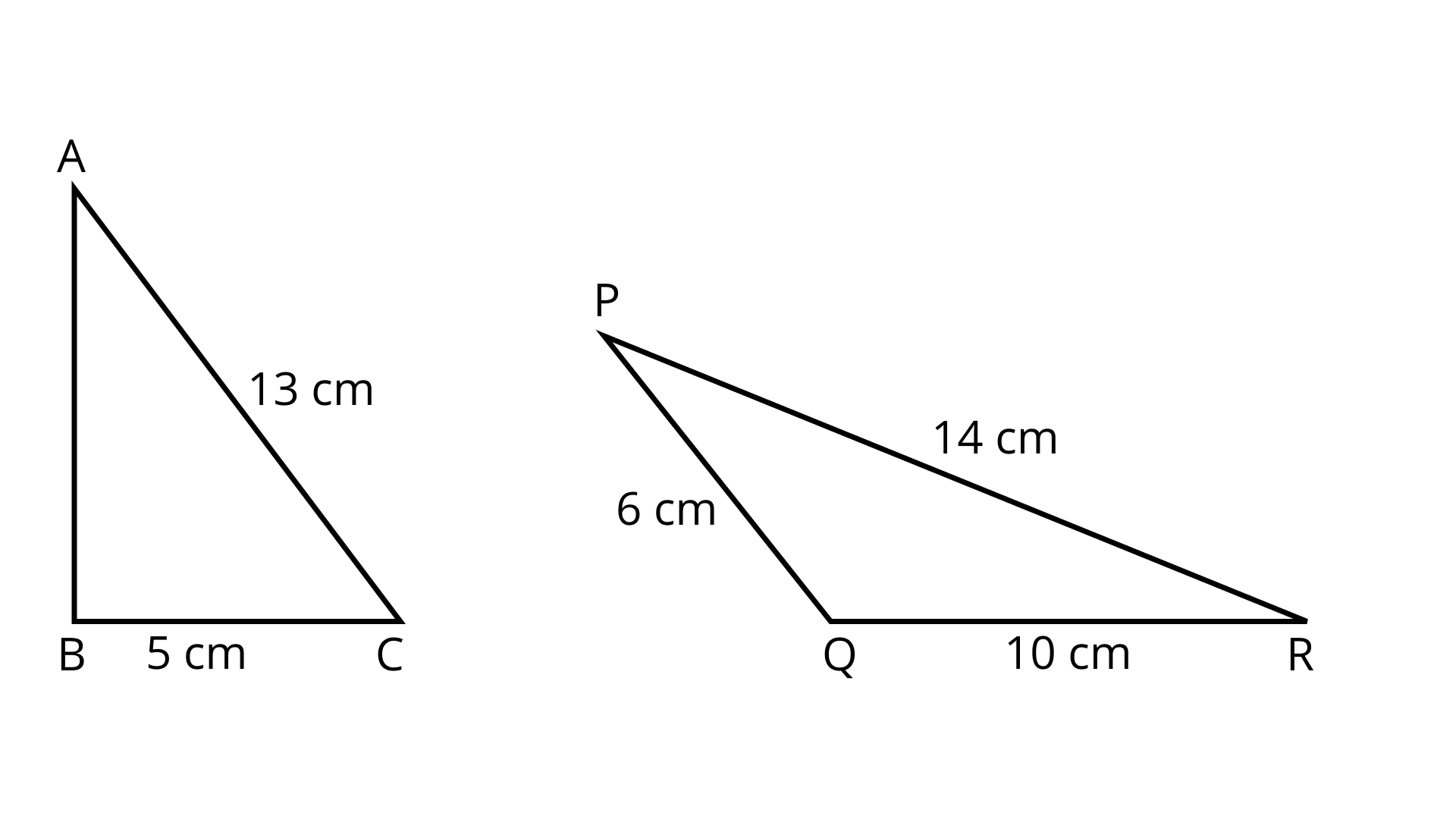
Ans: Given,

Perimeter of triangle ${\text{PQR}} = $ Perimeter of triangle ${\text{ABC}}$

Perimeter of triangle ${\text{PQR}} = 14 + 6 + 10 = 30\;{\text{cm}}$

Now,

Perimeter of triangle ${\text{ABC}} = {\text{AB}} + {\text{BC}} + {\text{CA}}$

$\Rightarrow AB + BC + CA = 30$

$\Rightarrow AB = 30 - 18$

$\Rightarrow AB = 12\;{\text{cm}}$

Hence, area of triangle ${\text{ABC}} = \dfrac{1}{2} \times 5 \times 12$

$ = 30\;{\text{c}}{{\text{m}}^2}$

86. Altitudes MN and MO of parallelogram MGHK are ${\mathbf{8\;cm}}$ and ${\mathbf{4\;cm}}$ long respectively (Fig. 9.40). One side ${\mathbf{GH}}$ is ${\mathbf{6\;cm}}$ long. Find the perimeter of MGHK.

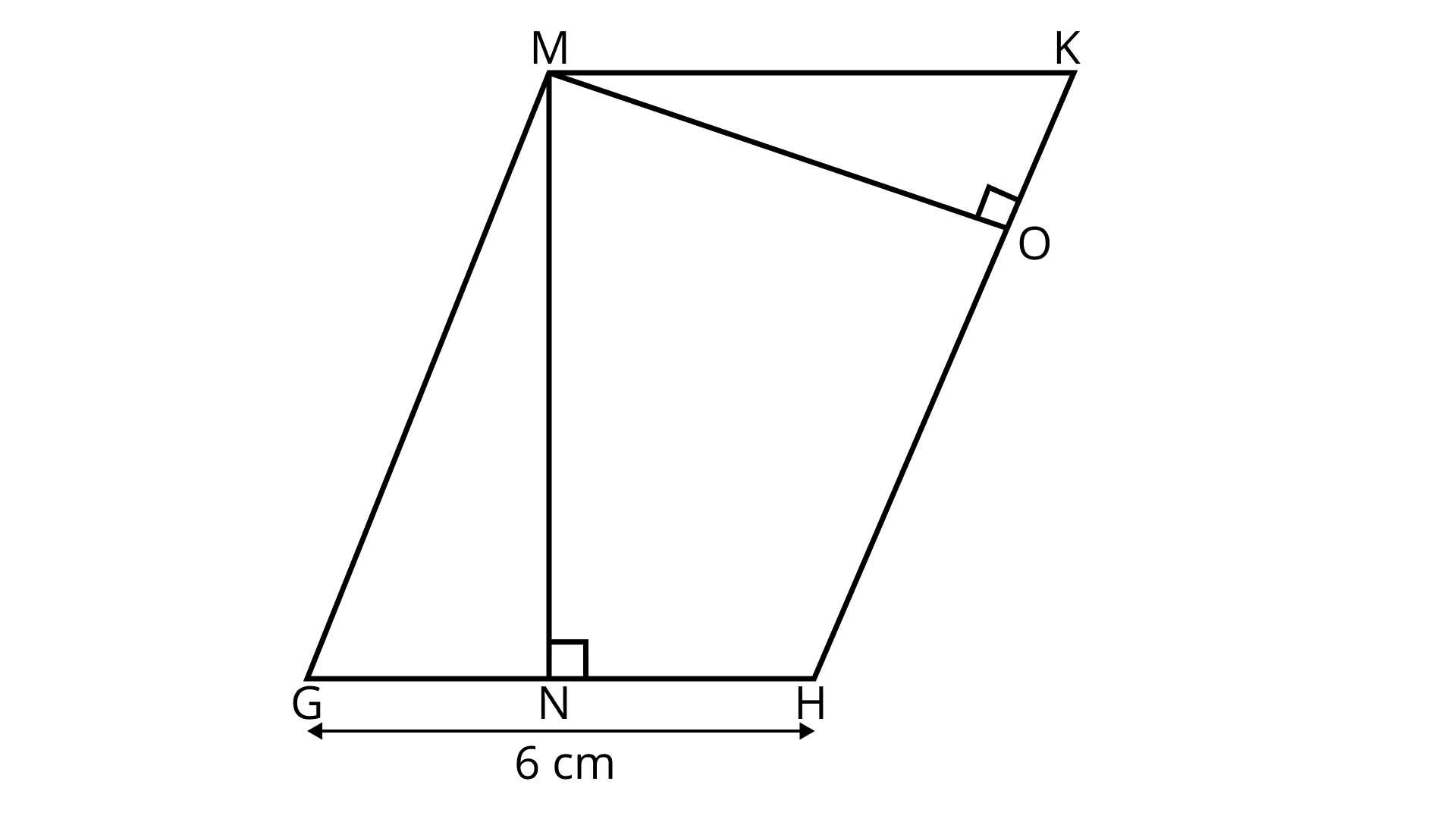
Ans: Given,

$MN = 8c{\text{m }}$

$MO = 4\;{\text{cm}}$

$GH = 6{\text{cm}}$

Now, area of parallelogram MGHK, when base is GH $ = GH \times MN$

$ = 6 \times 8 = 48\;{\text{c}}{{\text{m}}^2}$

Now, area of parallelogram MGHK, when base is HK

$48 = HK \times 4$

$HK = \dfrac{{48}}{4} = 12\;{\text{cm}}$

In parallelogram, opposite sides are equal

Thus, ${\text{GH}} = 6\;{\text{cm}} = {\text{MK}}$, and ${\text{MG}} = {\text{HK}} = 12\;{\text{cm}}$

Therefore, perimeter of parallelogram $ = 6 + 6 + 12 + 12$ 

$ = 36\;{\text{cm}}$

87. In Fig. 9.41, area of $\vartriangle {\mathbf{PQR}}$ is ${\mathbf{20\;c}}{{\mathbf{m}}^{\mathbf{2}}}$ and area of $\vartriangle {\mathbf{PQS}}$ is ${\mathbf{44\;c}}{{\mathbf{m}}^{\mathbf{2}}}$. Find the length RS, if ${\mathbf{PQ}}$ is perpendicular to ${\mathbf{QS}}$ and ${\mathbf{QR}}$ is ${\mathbf{5\;cm}}$.

Ans: Given,

Area of triangle PQR $ = 20$ sq. ${\text{cm}}$ 

Area of triangle PQS $ = 44$ sq. ${\text{cm}}$ 

Area of triangle PQR,

$20 = \dfrac{1}{2} \times PQ \times 5$

$\Rightarrow PQ = 8{\text{cm}}$

Area of triangle PQS,

$44 = \dfrac{1}{2} \times PQ \times QS$

$\Rightarrow QS = \dfrac{{44 \times 2}}{8} = 11{\text{cm}}$

Now, 

${\text{RS}} = {\text{QS}} - {\text{QR}}$

$ = 11 - 5$

$ = 6{\text{cm }}$

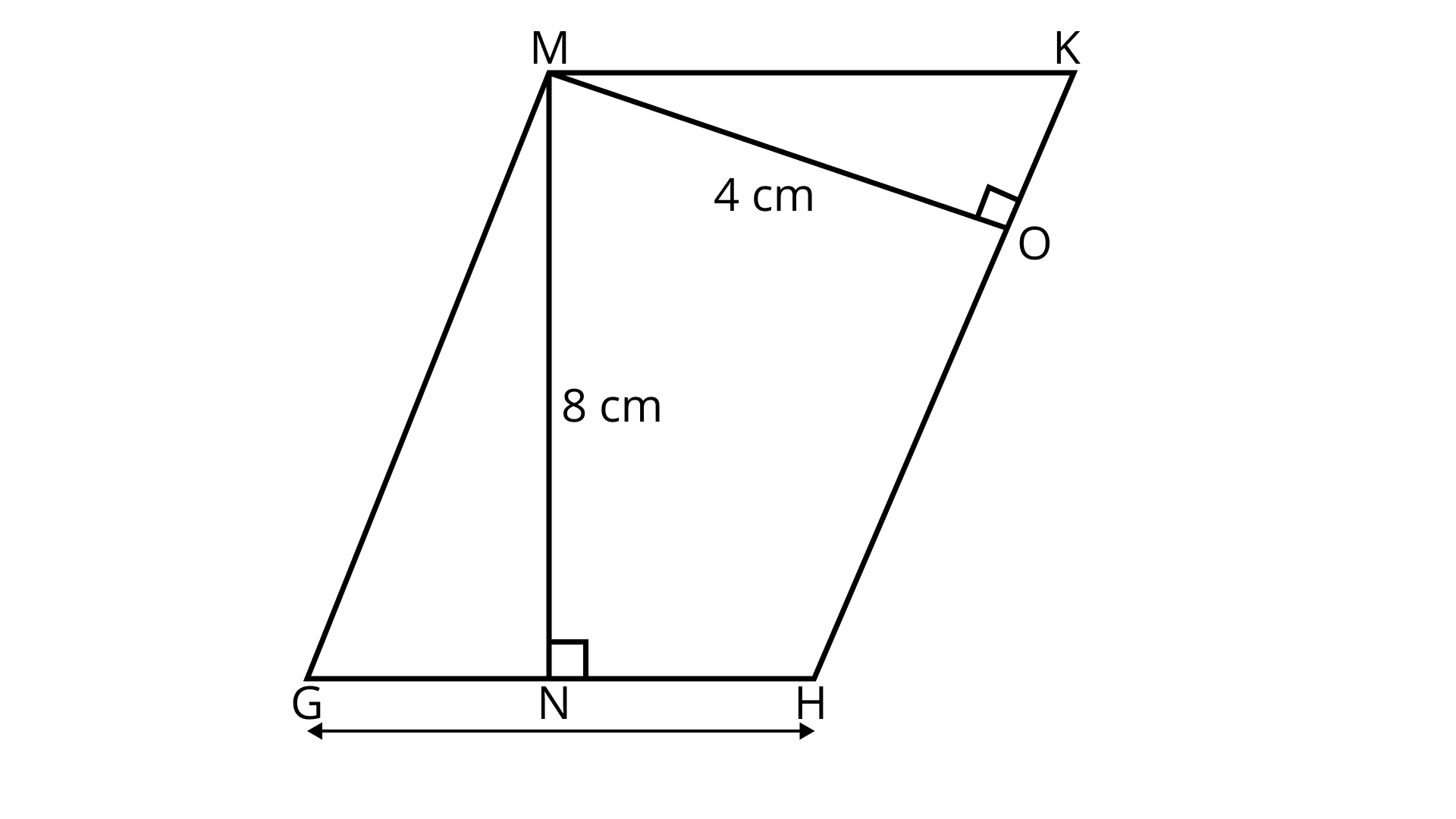
88. Area of an isosceles triangle is ${\mathbf{48\;c}}{{\mathbf{m}}^{\mathbf{2}}}$. If the altitude corresponding to the base of the triangle is ${\mathbf{8\;cm}}$, find the perimeter of the triangle.

Ans:

Given,

Area of triangle ${\text{ABC}} = 48$ sq. ${\text{cm}}$

Height $ = 8\;{\text{cm}}$

Area of triangle ${\text{ABC}}$,

$ \Rightarrow 48 = \dfrac{1}{2} \times BC \times AD$ 

$ \Rightarrow BC = \dfrac{{48 \times 2}}{8} = 12\;{\text{cm}}$

Now, in a isosceles triangle, $BD = DC = 6\;{\text{cm}}$

Applied Pythagoras theorem in triangle ADB

$A{B^2} = B{D^2} + A{D^2}$

$\Rightarrow A{B^2} = {6^2} + {8^2}$

$\Rightarrow A{B^2} = 36 + 64$

$\Rightarrow AB = 10\;{\text{cm}}$

Now, perimeter of triangle $ = {\text{AB}} + {\text{AC}} + {\text{BC}}$

$ = 10 + 10 + 12$

$ = 32\;{\text{cm}}$

89. Perimeter of a parallelogram shaped land is ${\mathbf{96\;m}}$ and its area is \[{\mathbf{270}}\]square metres. If one of the sides of this parallelogram is ${\mathbf{18\;m}}$, find the length of the other side. Also, find the lengths of altitudes ${\mathbf{l}}$ and $\operatorname{m} $ (Fig. 9.42).

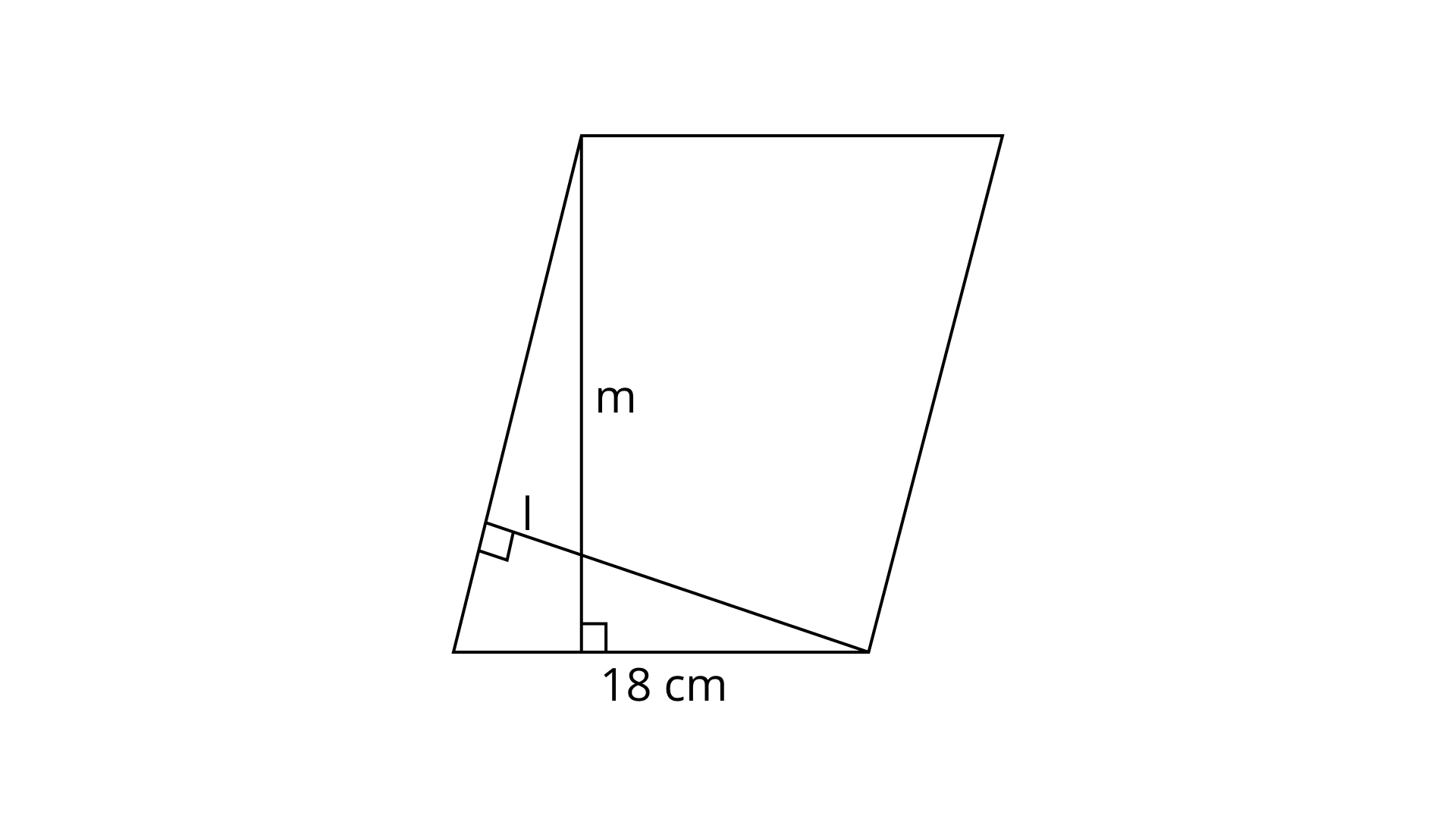
Ans: Given,

Perimeter of parallelogram $ = 96\;{\text{cm}}$

Area of parallelogram $ = 270$ sq. ${\text{m}}$

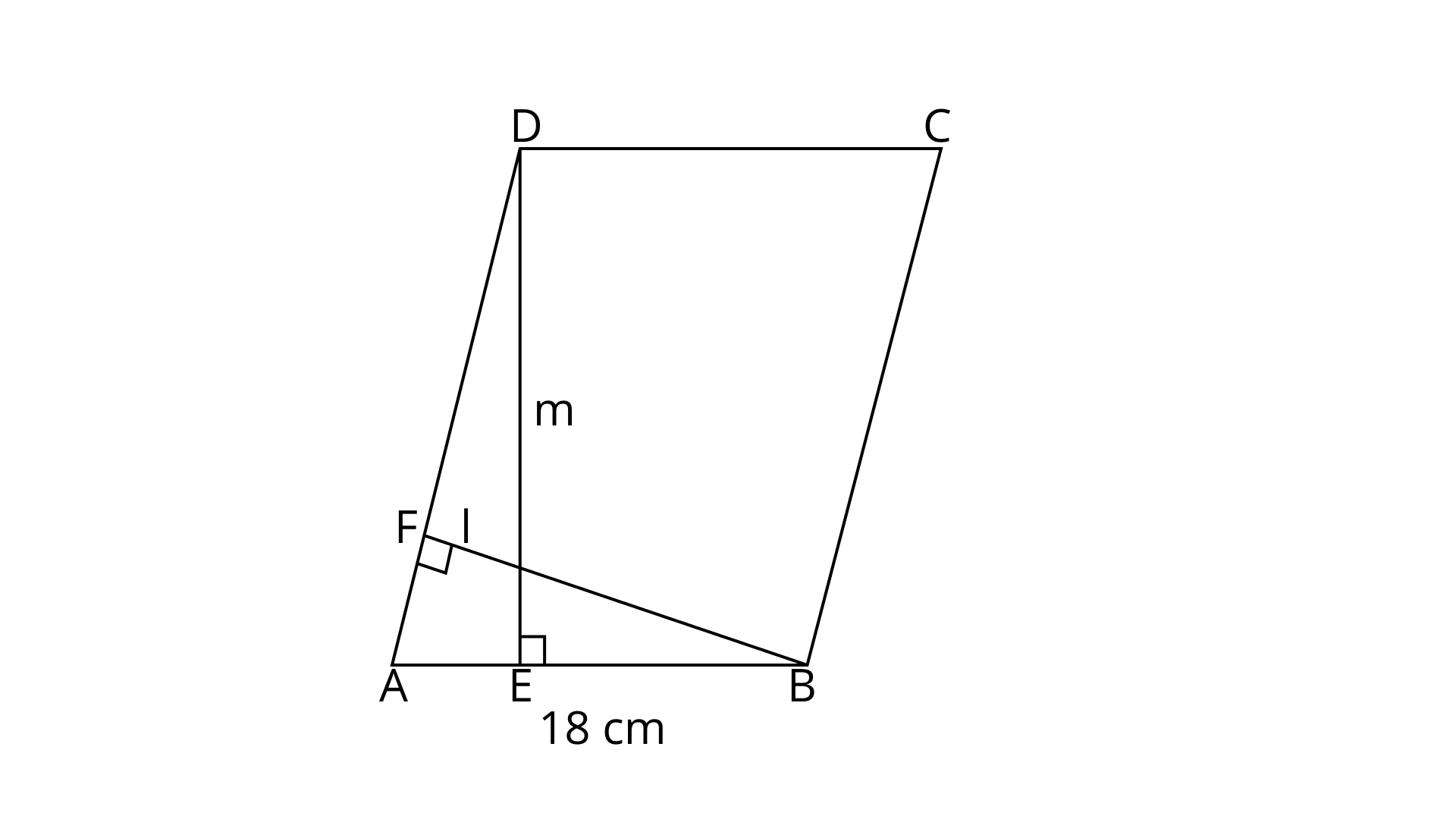
In parallelogram ${\text{ABCD}},{\text{AB}} = {\text{CD}} = 18\;{\text{m}}$ and ${\text{AD}} = {\text{BC}}$

As we know perimeter of a parallelogram ${\text{ABCD}}$,

${\text{AB}} + {\text{BC}} + {\text{CD}} + {\text{AD}}$

$\Rightarrow 96 = 18 + AD + 18 + AD$

$\Rightarrow 96 = 36 + 2AD$

$\Rightarrow AD = BC = 30\;{\text{cm}}$

Now, area of parallelogram ABCD,

\[270 = AB \times DE\]

\[\Rightarrow DE = \dfrac{{270}}{{18}}\]

\[\Rightarrow DE = 15{\text{cm }}\]

Now, area of parallelogram ${\text{ABCD}}$, 

$ \Rightarrow 270 = 30 \times l$

$\Rightarrow l = \dfrac{{270}}{{30}}{\text{ }}$

$\Rightarrow l = 9m{\text{ }}$

90. Area of a triangle ${\mathbf{PQR}}$ right-angled at ${\mathbf{Q}}$ is ${\mathbf{60\;c}}{{\mathbf{m}}^{\mathbf{2}}}$ (Fig. 9.43). If the smallest side is ${\mathbf{8\;cm}}$ long, find the length of the other two sides.

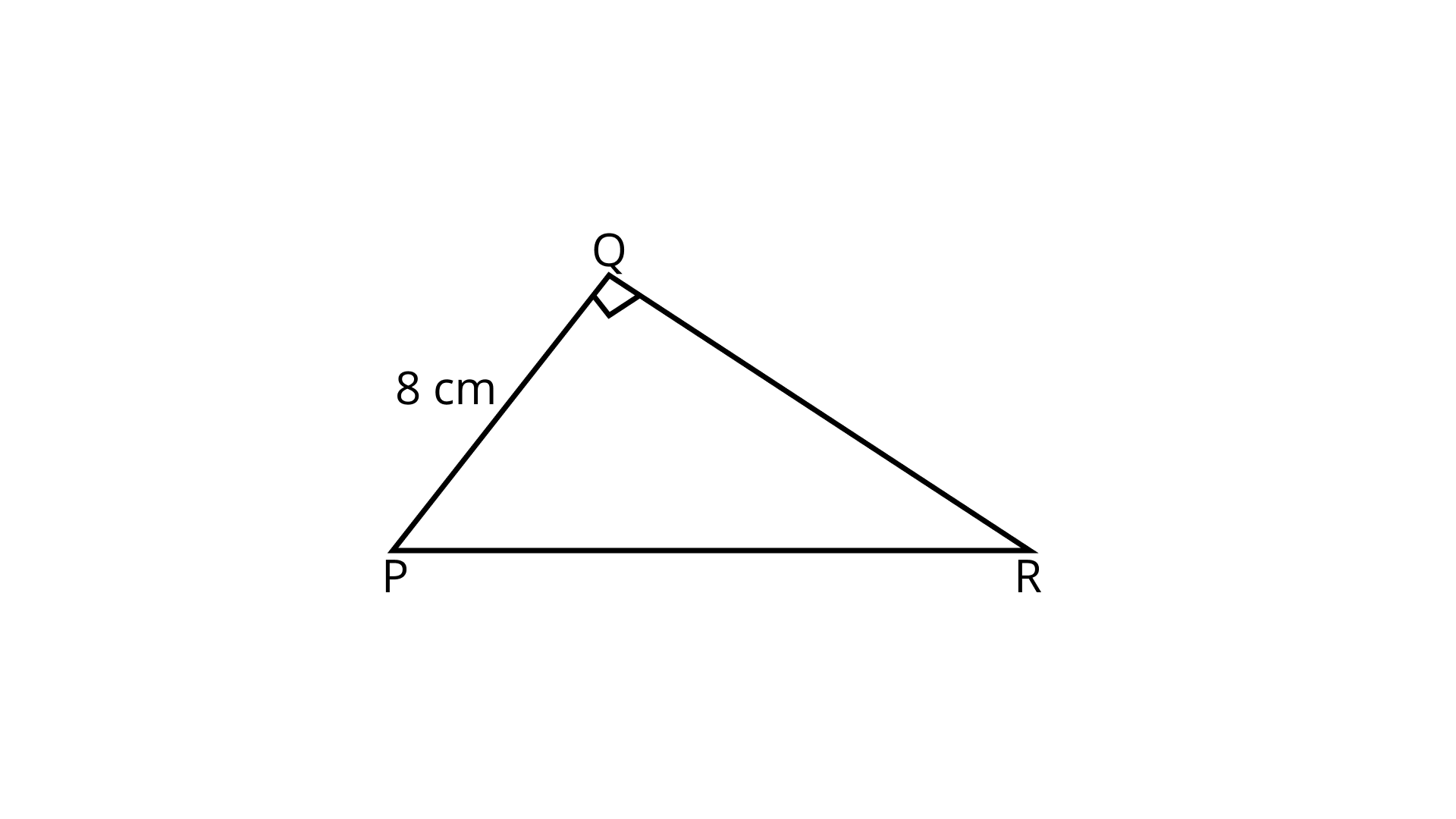
Ans: Given,

Area of triangle ${\text{PQR}} = 60{\text{sq}}.{\text{cm}}$

Side $(PQ) = 8\;{\text{cm}}$

Area of triangle PQR,

$ \Rightarrow 60 = \dfrac{1}{2} \times 8 \times QR$

$ \Rightarrow QR = \dfrac{{60 \times 2}}{8} = 15\;{\text{cm}}$

Applied Pythagoras theorem in triangle PQR 

$ \Rightarrow P{R^2} = P{Q^2} + Q{R^2}$

$ \Rightarrow P{R^2} = {8^2} + {15^2}$

$ \Rightarrow P{R^2} = 64 + 225$

$ \Rightarrow PR = 17\;{\text{cm}}$

Therefore, $15\;{\text{cm}}$ and $17\;{\text{cm}}$ are lengths of sides of a triangle.

91. In Fig. 9.44 a rectangle with perimeter ${\mathbf{264\;cm}}$ is divided into five congruent rectangles. Find the perimeter of one of the rectangles.

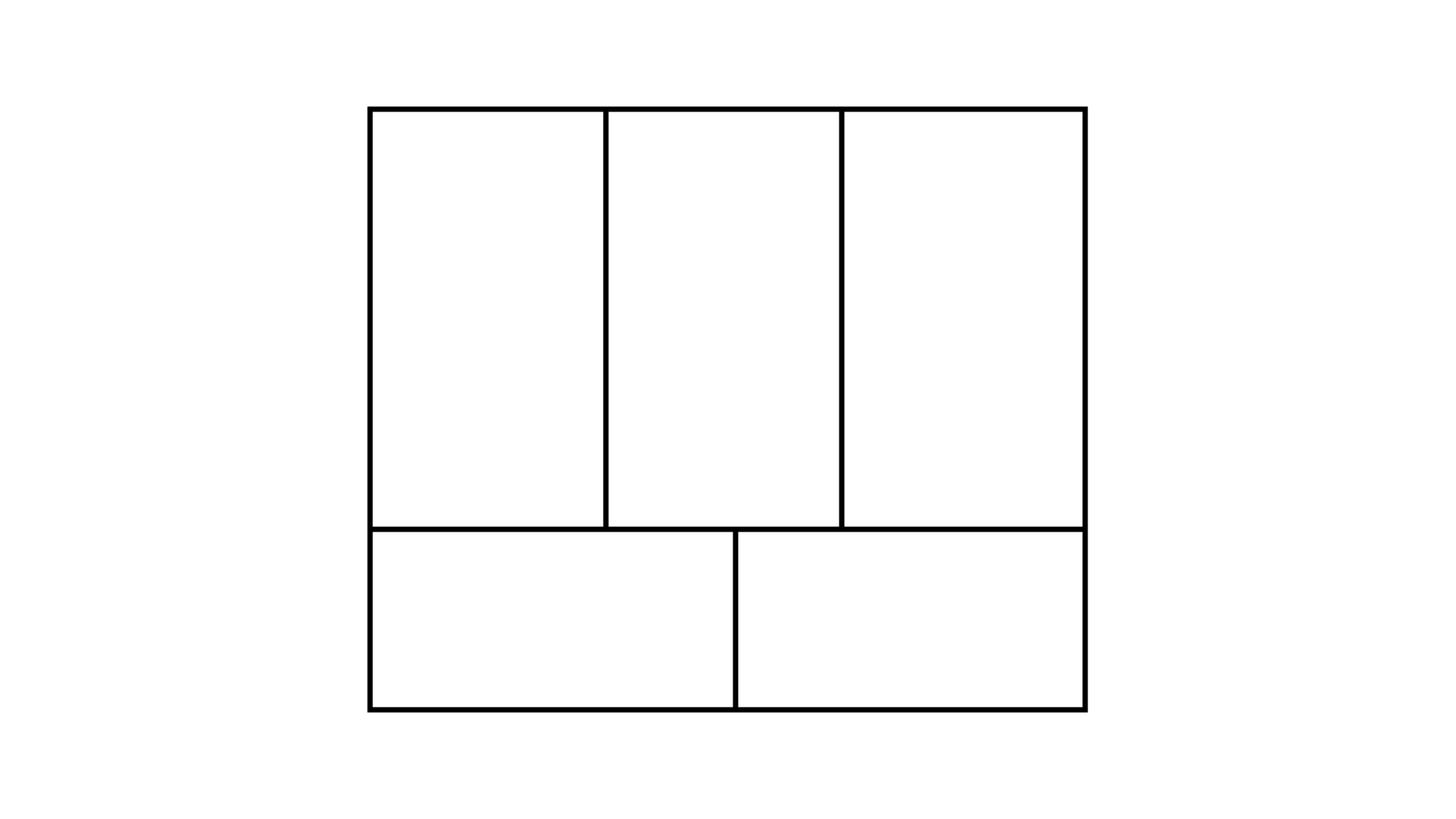
Ans: Let ${\text{b}}$ and l be the breadth and length of each rectangle. Given, perimeter of a rectangle $ = 264\;{\text{cm}}$

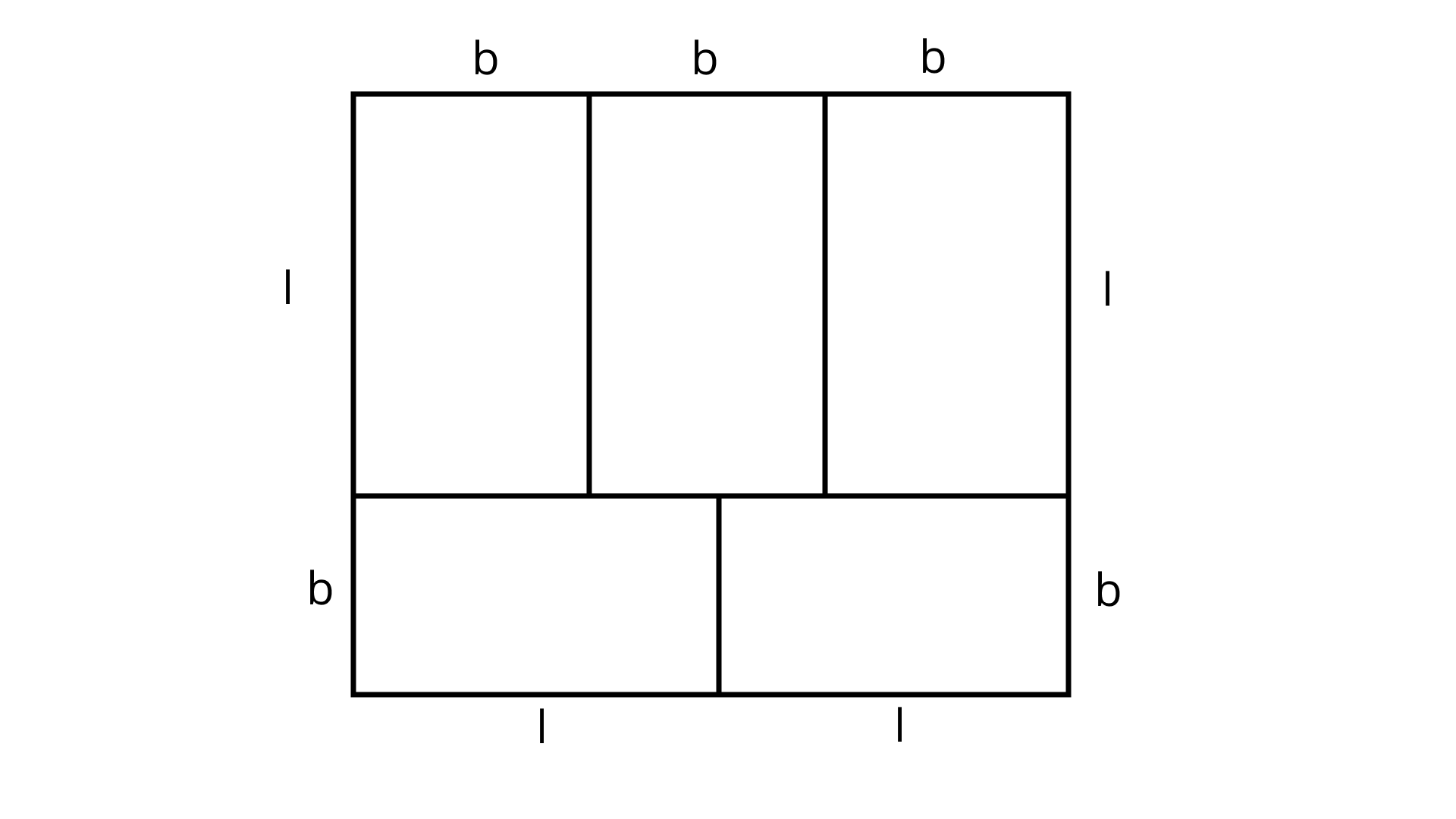
According to the figure,

$4l + 5b = 264$ & $2l = 3b$

Now, put the value of $3\;{\text{b}}$ into equation 2 from equation 1

$ \Rightarrow 2 \times 3b + 5b = 264$

$ \Rightarrow (6 + 5)b = 264$

$ \Rightarrow b = \dfrac{{264}}{{11}}$

$ \Rightarrow b = 24{\text{cm}}$

$l = \dfrac{{3b}}{2} = \dfrac{{3 \times 24}}{2} = 36\;{\text{cm}}$

Therefore, perimeter of the rectangle

$ = 2(\operatorname{l}  + b)$

\[ = 2(36 + 24)\]

\[ = 120{\text{cm}}\]

92. Find the area of a square inscribed in a circle whose radius is ${\mathbf{7\;cm}}$ (Fig. 9.45).

Hint: Four right-angled triangles joined at right angles to form a square

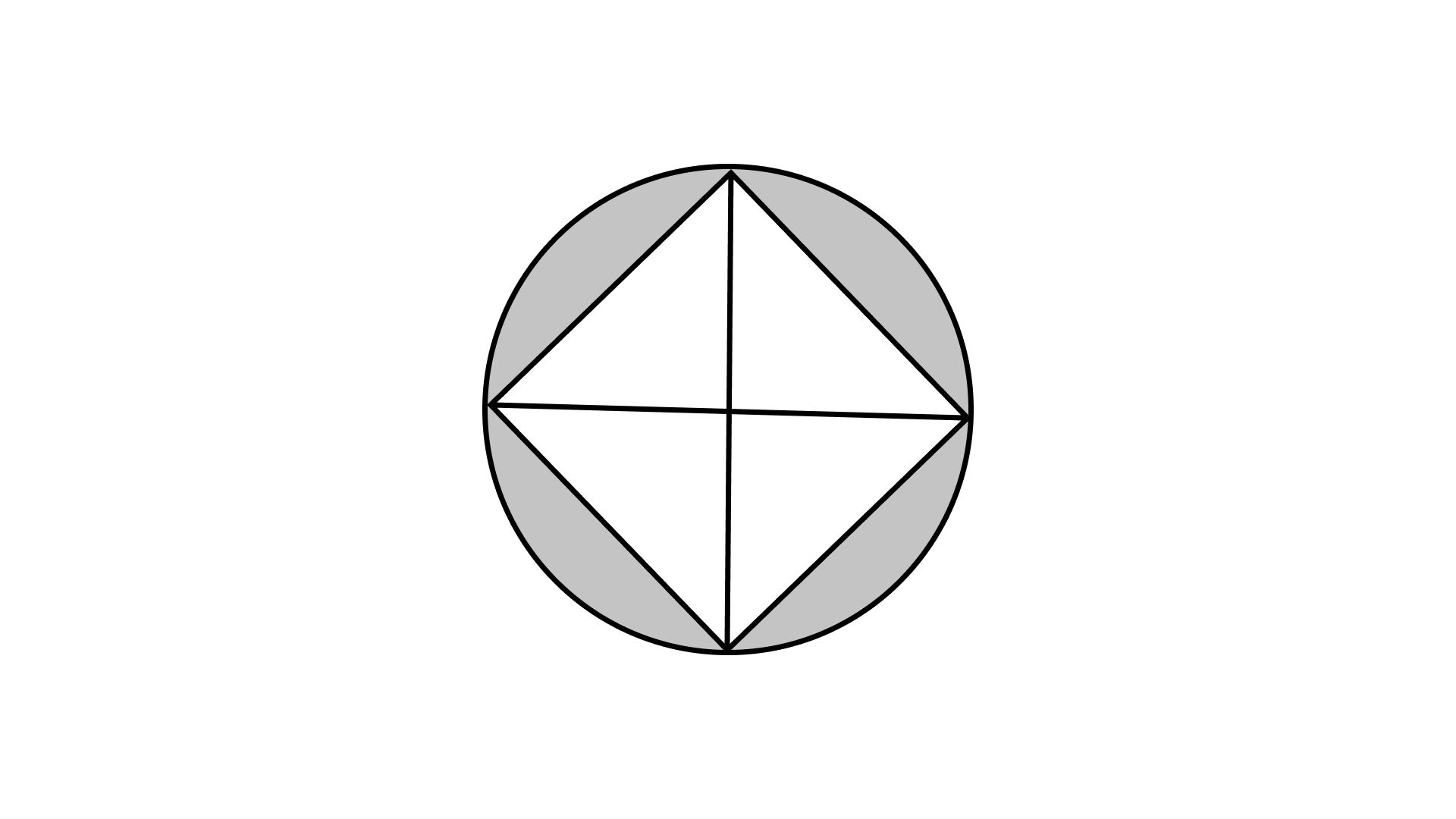
Ans: 

${\text{ABCD}}$ is a square.

Area of square ${\text{ABCD}} = 4$ times of area of right-angled triangle AOB

Now, Area of square ${\text{ABCD}}$

$ = 4 \times \left( {\dfrac{1}{2} \times AO \times BO} \right)$ 

$ = 2 \times 7 \times 7 = 98\;{\text{c}}{{\text{m}}^2}$

Therefore, the area of the inscribed square is $98\;{\text{c}}{{\text{m}}^2}$.

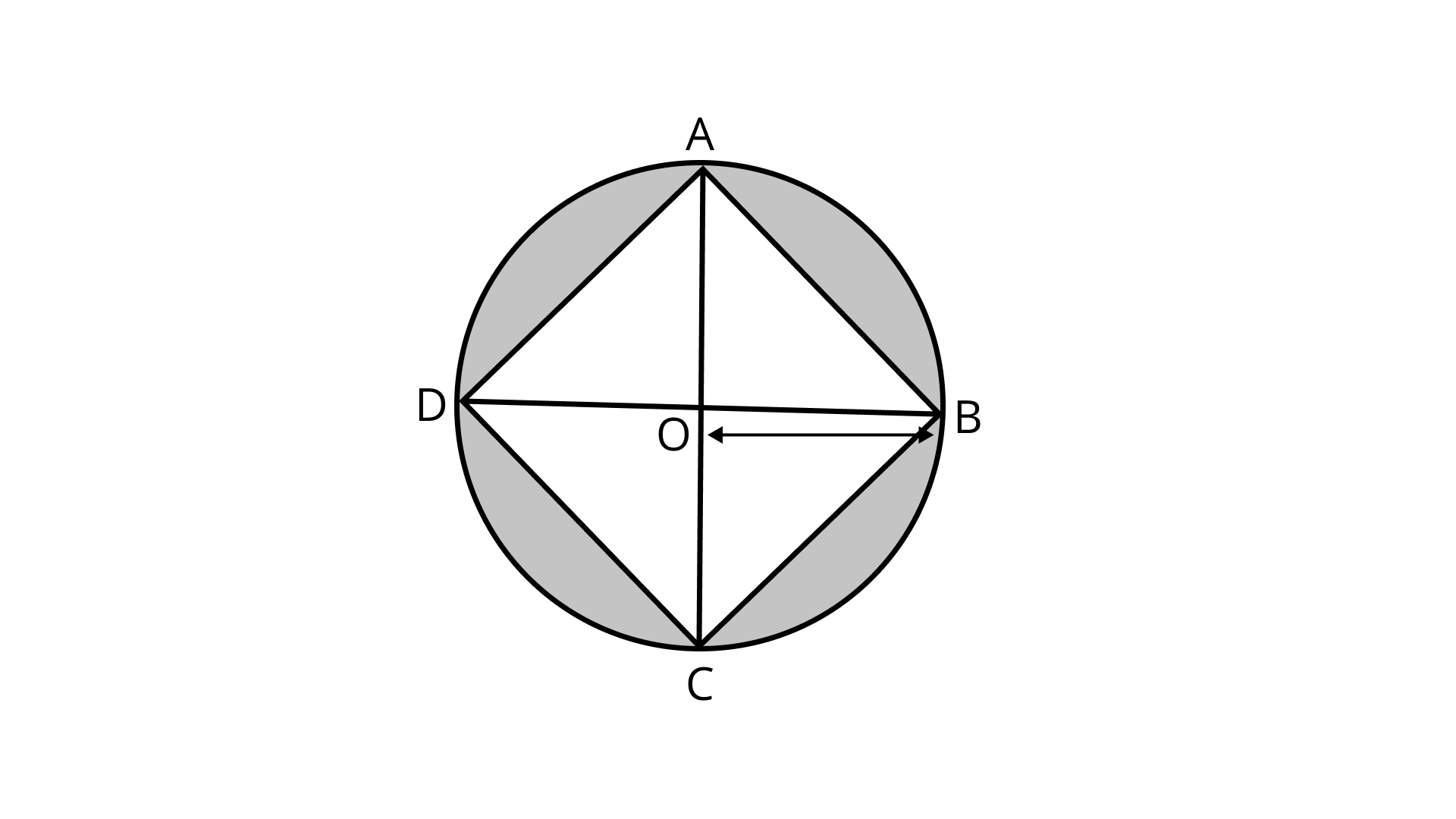
93. Find the area of the shaded portion in question 92.

Ans: ${\text{ABCD}}$ is a square.

Area of square ${\text{ABCD}} = 4$ times of area of right-angled triangle AOB

Now, Area of square ABCD

$ = 4 \times \left( {\dfrac{1}{2} \times AO \times BO} \right)$

$ = 2 \times 7 \times 7 = 98\;{\text{c}}{{\text{m}}^2}$

Now, area of shaded portion

$ = \pi {r^2} - 98$

$ = \dfrac{{22}}{7} \times 7 \times 7 - 98$

$ = 154 - 98$

$ = 56\;{\text{c}}{{\text{m}}^2}$

In Questions 94 to 97 find the area enclosed by each of the following figures:

94.

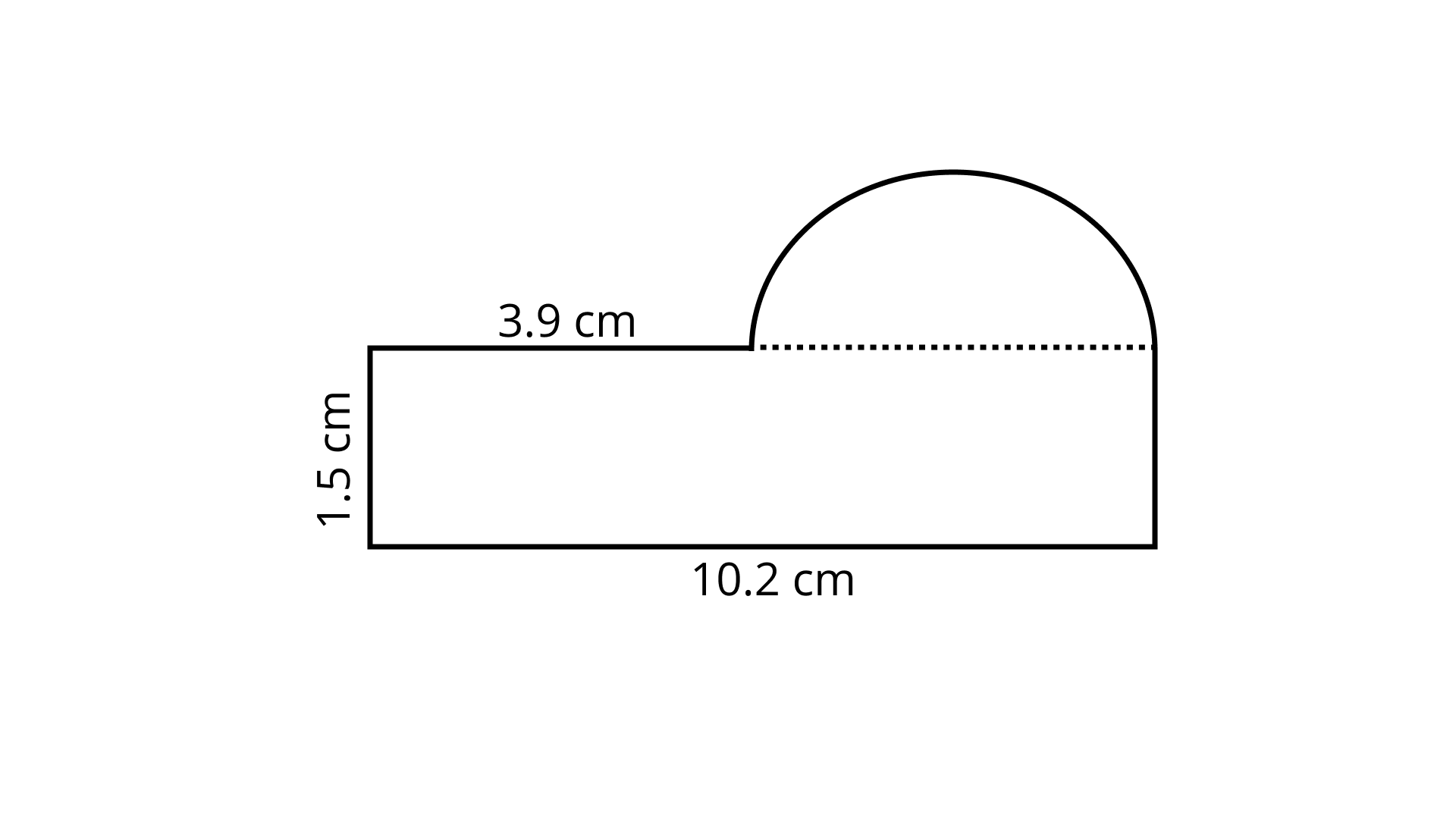
Ans: The Sample contains a semi-circle and a rectangle.

Area of rectangle $ = 10.2 \times 1.5 = 15.3\;{\text{c}}{{\text{m}}^2}$

Diameter of semi-circle $ = 10.2 - 3.9 = 6.3\;{\text{cm}}$

Radius $ = 3.15\;{\text{cm}}$

Area of semi-circle

$ = \dfrac{1}{2}\pi {r^2} = \dfrac{{22}}{7} \times \dfrac{1}{2} \times 3.15 \times 3.15 = 15.59\;{\text{c}}{{\text{m}}^2}$

Therefore, total area $ = 15.3 + 15.59 = 30.89\;{\text{c}}{{\text{m}}^2}$.

95.

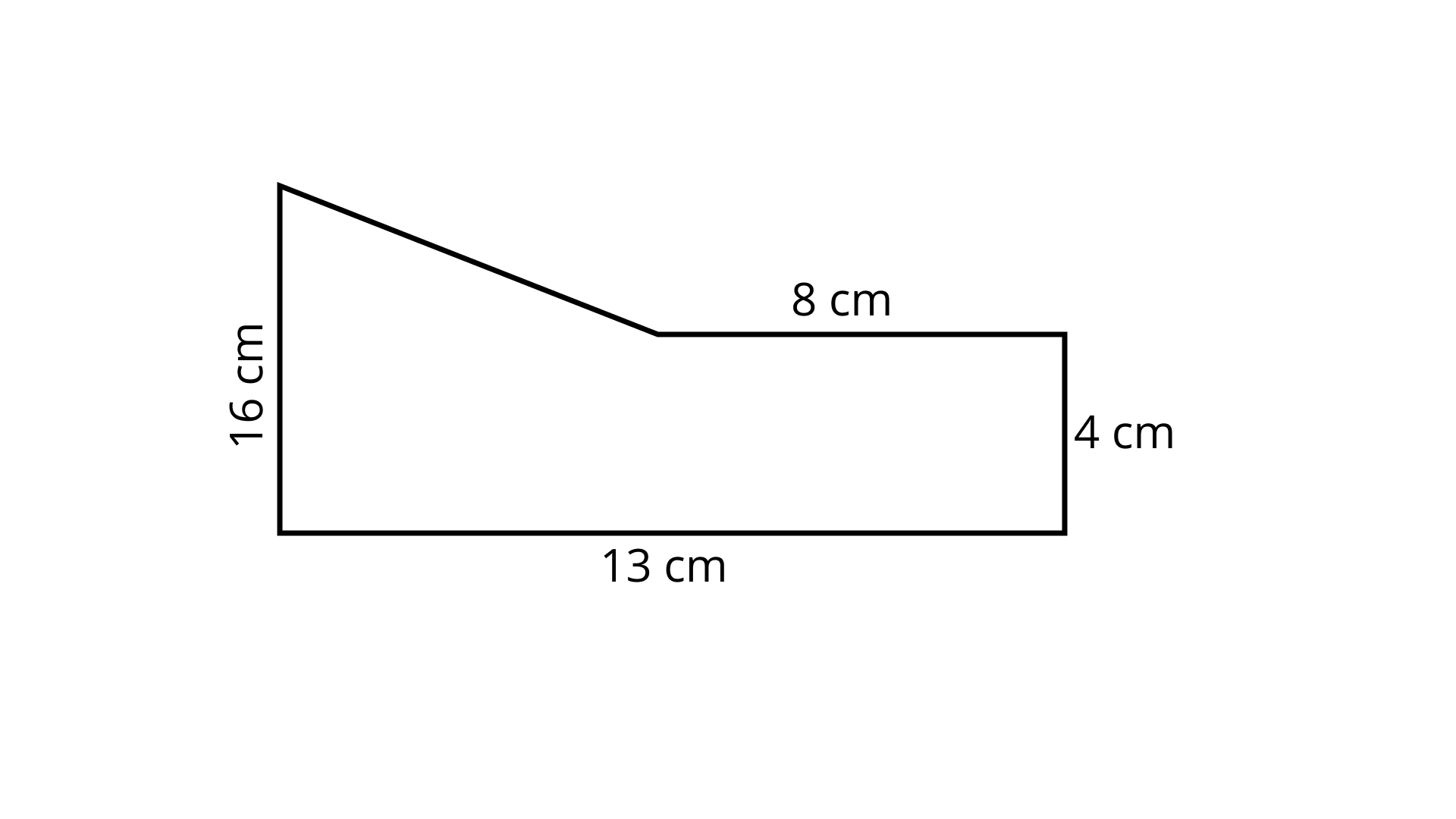
Ans: The Sample contains a triangle and a rectangle.

Area of rectangle $ = 13 \times 4 = 52\;{\text{c}}{{\text{m}}^2}$ 

Area of triangle $ = \dfrac{1}{2} \times 5 \times 12 = 30\;{\text{c}}{{\text{m}}^2}$

Therefore, the total area enclosed in shape $ = 52 + 30 = 82\;{\text{c}}{{\text{m}}^2}$.

96. 

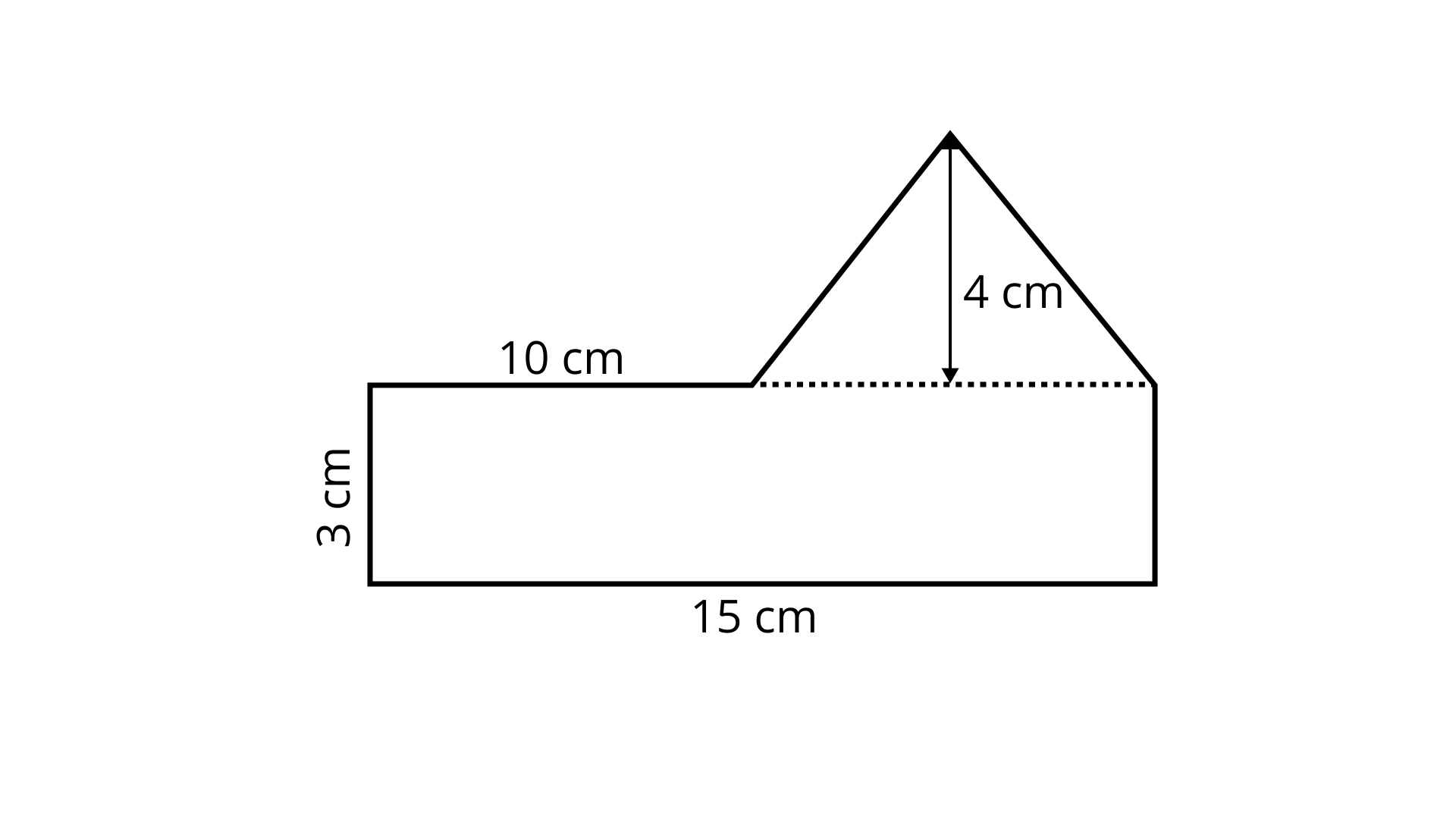
Ans: The Sample contains a triangle and a rectangle.

Area of rectangle $ = 15 \times 3 = 45\;{\text{c}}{{\text{m}}^2}$

According to the figure the base ${\text{BE}} = 15 - 10 = 5\;{\text{cm}}$

Now, area of triangle $ = \dfrac{1}{2} \times 5 \times 4 = 10\;{\text{c}}{{\text{m}}^2}$

Therefore, the total area enclosed in shape $ = 45 + 10 = 55\;{\text{c}}{{\text{m}}^2}$.

97. 

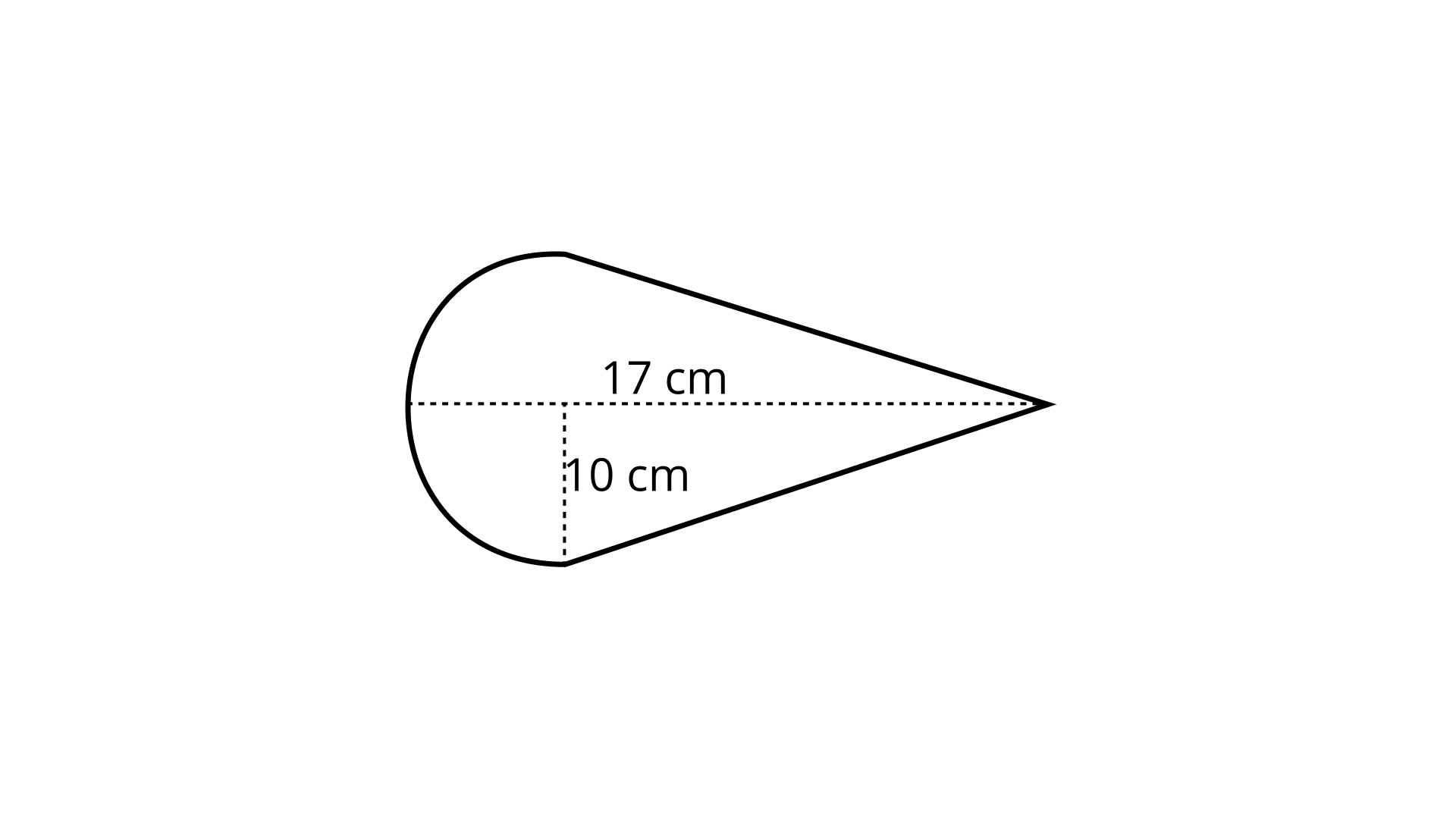
Ans: The Sample contains a semi-circle and a triangle. 

Area of semi-circle $=\dfrac{1}{2}\pi{r^{2}}=\dfrac{1}{2}\times\dfrac{22}{7}\times 100=\dfrac{1100}{7}$

Now, area of triangle $ = \dfrac{1}{2} \times 20 \times 7 = 70\;{\text{c}}{{\text{m}}^2}$

Therefore, total area enclosed in shape

$ = \dfrac{{1100}}{7} + 70$

$ = \dfrac{{1100 + 490}}{7}$

$ = \dfrac{{1590}}{7}$

$ = 227{\text{c}}{{\text{m}}^2}$

In Questions 98 and 99 find the areas of the shaded region:

98.

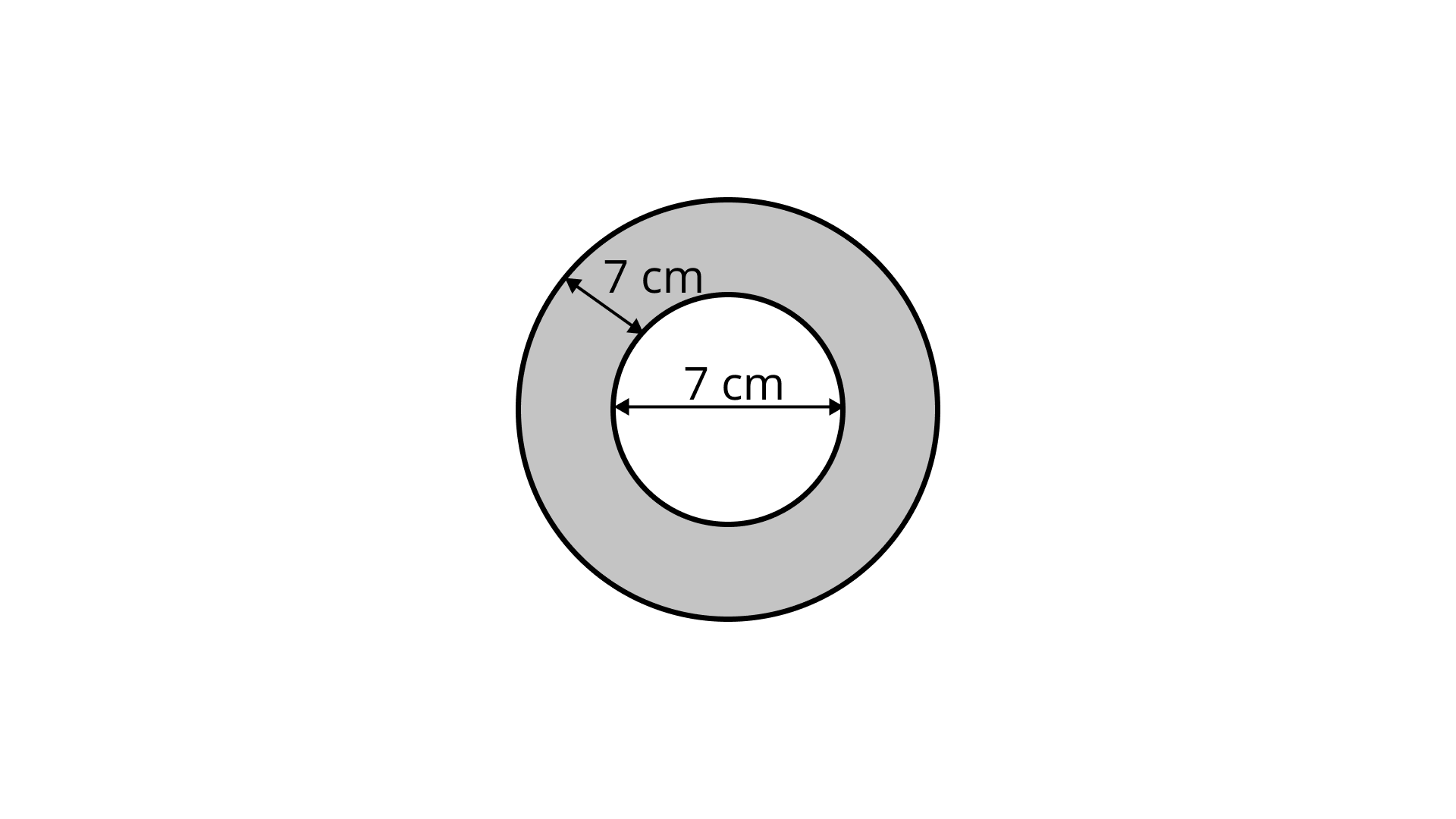
Ans: Let $R$ be radius of bigger circle and $r$ be radius of smaller circle,

From the figure,

$ \Rightarrow r = \dfrac{7}{2}{\text{cm }}$

$ \Rightarrow R = \dfrac{7}{2} + 7 = \dfrac{{21}}{2}{\text{cm}}$

Now, area of shaded region $ = $ area of bigger circle $ - $ area of smaller circle 

$ = \pi \left( {{R^2} - {r^2}} \right)$

$ = \dfrac{{22}}{7} \times \left( {\dfrac{{21}}{2} \times \dfrac{{21}}{2} - \dfrac{7}{2} \times \dfrac{7}{2}} \right){\text{ }}$

$ = \dfrac{{22}}{7} \times \dfrac{{392}}{4}$

$ = 308{\text{c}}{{\text{m}}^2}{\text{ }}$

Therefore, $308\;{\text{c}}{{\text{m}}^2}$ is the area of the shaded portion.

99.

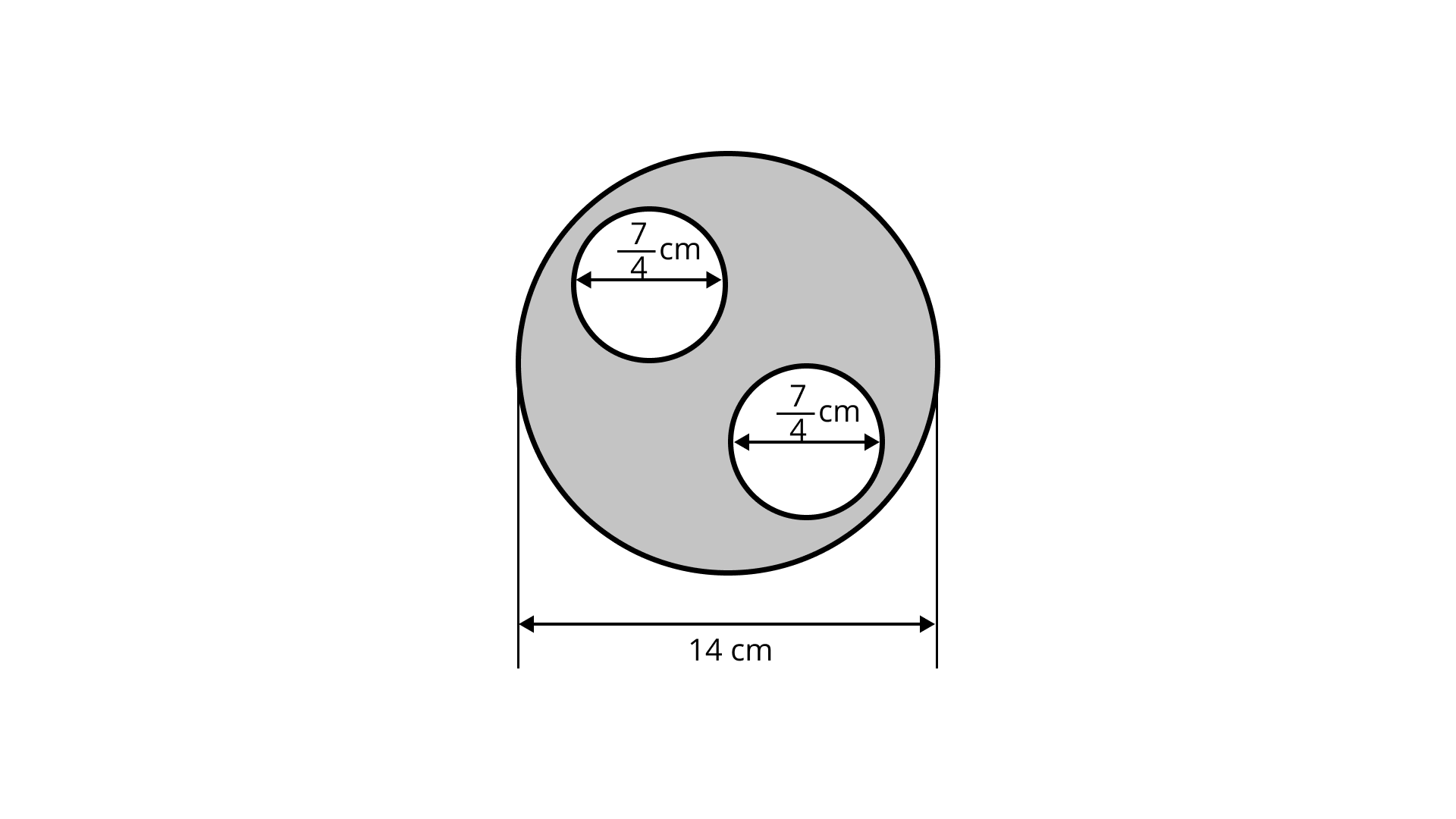
Ans: Diameter of the complete circle $ = 14\;{\text{cm}}$

Radius $ = 7\;{\text{cm}}$

From the figure,

Area of the complete circle $ = \dfrac{{22}}{7} \times 7 \times 7 = 154\;{\text{c}}{{\text{m}}^2}$

Diameter of the smaller circle $ = \dfrac{7}{4}$

$ \Rightarrow \operatorname{radius} (r) = \dfrac{7}{8}\;{\text{cm}}$

Area of two smaller circles

$ = 2 \times \pi {r^2}{\text{ }}$

$ = 2 \times \dfrac{{22}}{7} \times \dfrac{7}{8} \times \dfrac{7}{8}$

$ = \dfrac{{77}}{{16}}{\text{c}}{{\text{m}}^2}$

Now, area of shaded portion = area of complete circle area of two smaller circles

$ = 154 - \dfrac{{77}}{{16}}$

$ = \dfrac{{2464 - 77}}{{16}}$

$ = \dfrac{{2387}}{{16}}$

$ = 149\dfrac{3}{{16}}{\text{c}}{{\text{m}}^2}$

Therefore, $149\dfrac{3}{{16}}\;{\text{c}}{{\text{m}}^2}$ is the area of the shaded portion.

100. A circle with radius \[16{\text{ }}{\mathbf{cm}}\] is cut into four equal parts and rearranged to form another shape as shown in Fig. 9.52:

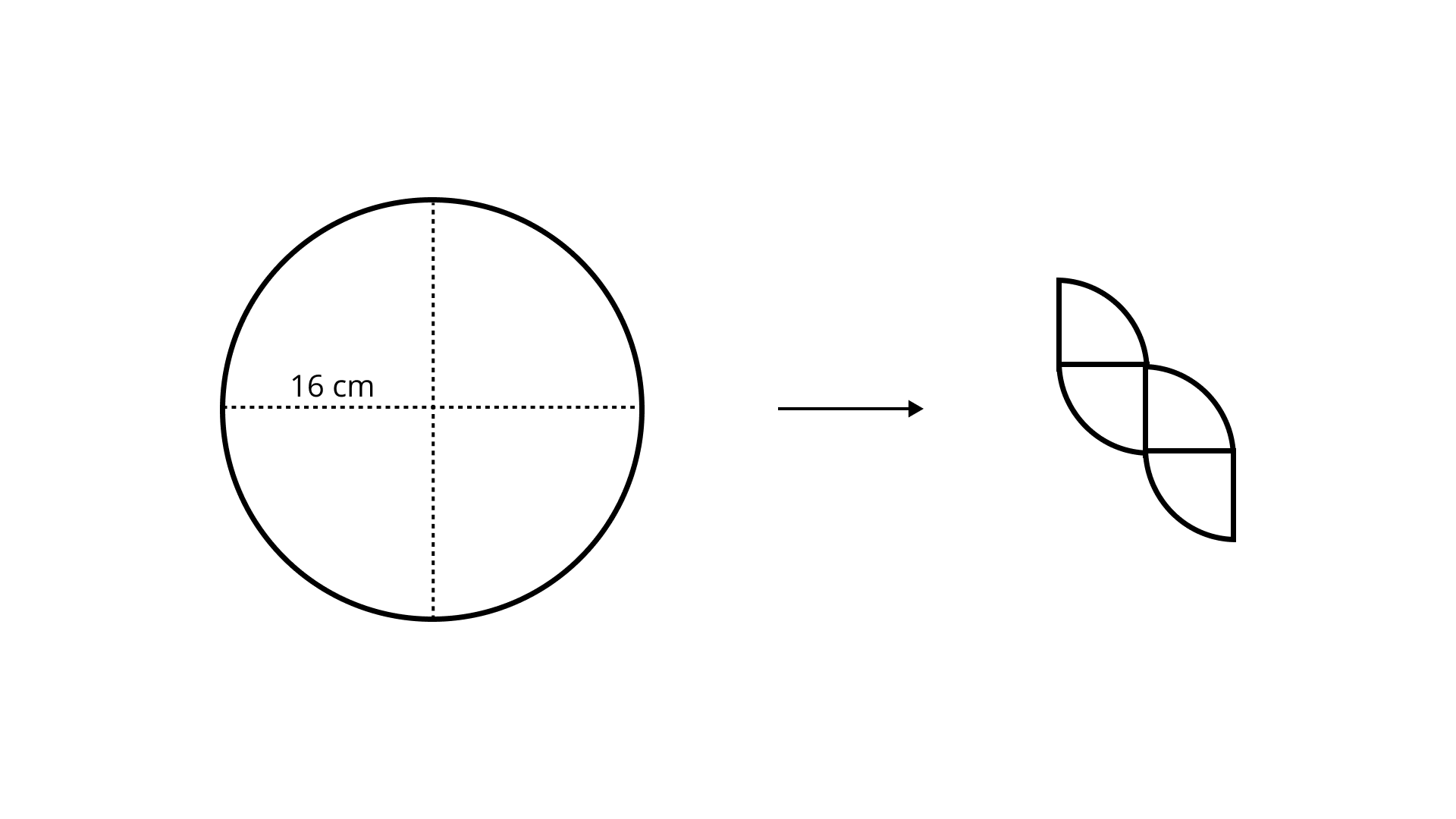
Does the perimeter change? If it does change, by how much does it increase or decrease?

Ans: Yes, the perimeter changes. 

Radius of circle $ - 16\;{\text{cm}}$

Perimeter of the circle $ = 2 \times \dfrac{{22}}{7} \times 16$

$ = 100.57\;{\text{cm}}$

Perimeter of new figure $ = 4$quarter circle$+2$radius

= Perimeter of circle$+2$radius

$ = 100.57 + 2 = 16 = 132.57\;{\text{cm}}$

Now the increase in perimeter $ = (132.57 - 100.57){\text{cm}} = 32\;{\text{cm}}$

101. A large square is made by arranging a small square surrounded by four congruent rectangles as shown in Fig. If the perimeter of each of the rectangles is \[16{\text{ }}{\mathbf{cm}}\], find the area of the large square.

Ans:

Let $b$ and $l$ be the breadth and length of the rectangle. 

Given, perimeter of one rectangle $ = 16\;{\text{cm}}$ 

$ \Rightarrow 2(l + b) = 16\;{\text{cm}}$

$ \Rightarrow l + b = 8\;{\text{cm}}$

As the side of larger square is $(l + b)$

Therefore, area $ = {(l + b)^2} = {8^2} = 64\;{\text{c}}{{\text{m}}^2}$

102. \[{\mathbf{ABCD}}\] is a parallelogram in which \[{\mathbf{AE}}\] is perpendicular to \[{\mathbf{CD}}\] (Fig.). Also\[{\mathbf{AC  =  5 cm, DE  =  4 cm}}\], and the area of triangle \[{\mathbf{AED  =  6 c}}{{\mathbf{m}}^{\mathbf{2}}}\]. Find the perimeter and area of \[{\mathbf{ABCD}}\].

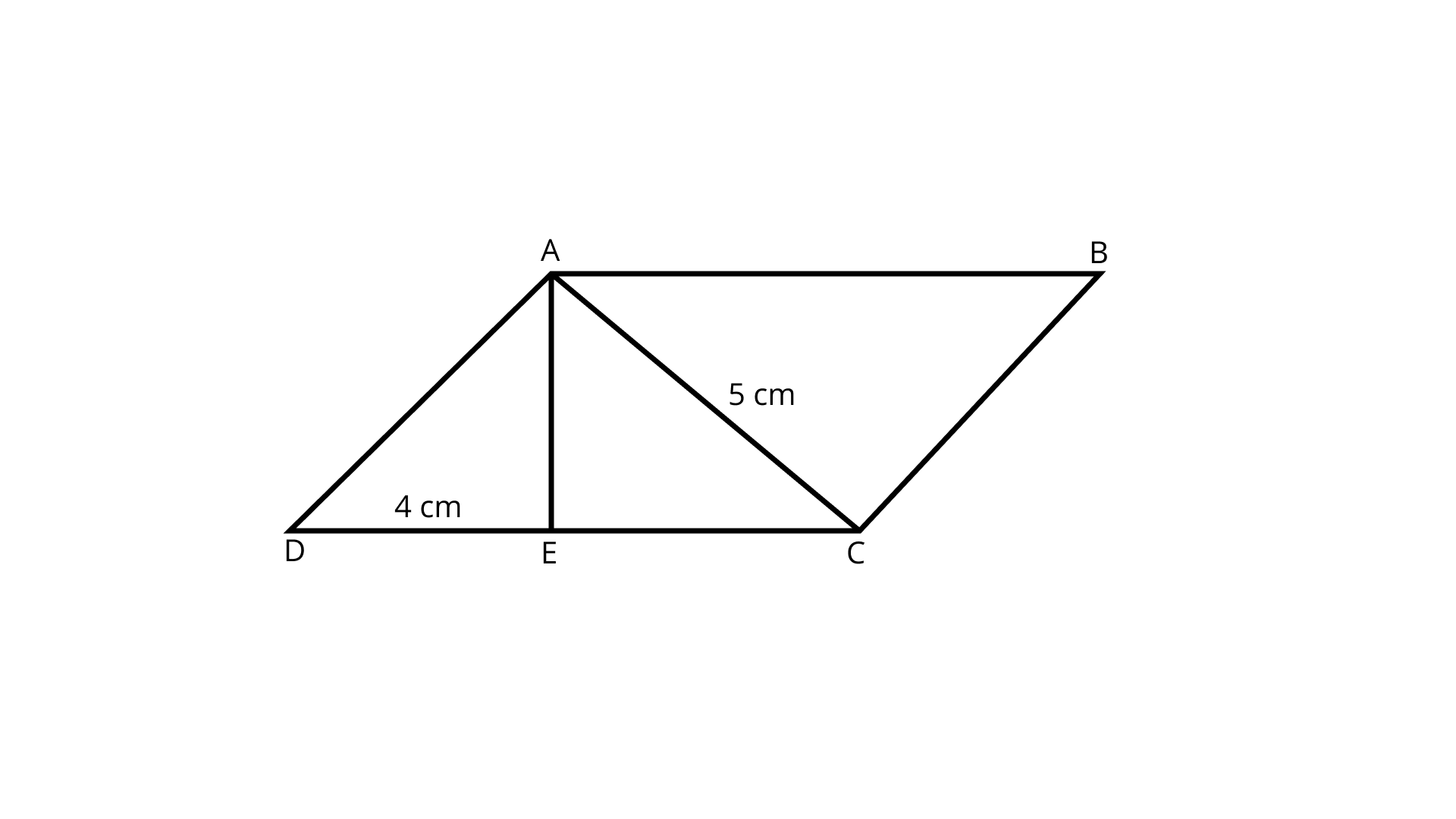
Ans: Given that,

Area of triangle ${\text{AED}} = 6{\text{sq}}.{\text{cm}}$

${\text{AC}} = 5\;{\text{cm}},{\text{DE}} = 4\;{\text{cm}}$

Area of triangle \[{\text{AED}}\]

$ \Rightarrow 6 = \dfrac{1}{2} \times 4 \times AE$

$ \Rightarrow AE = \dfrac{{6 \times 2}}{4} = 3\;{\text{cm}}$

Now, area of right-angled triangle\[{\text{AEC}}\],

${\text{AE}} = 3\;{\text{cm}},{\text{AC}} = 5\;{\text{cm}}$

\[ \Rightarrow {\text{E}}{{\text{C}}^{\text{2}}}{\text{ = A}}{{\text{C}}^{\text{2}}} - {\text{A}}{{\text{E}}^{\text{2}}}\]

$ \Rightarrow {\text{E}}{{\text{C}}^{\text{2}}} = {5^2} - {3^2}$

$ \Rightarrow {\text{E}}{{\text{C}}^{\text{2}}} = 16$

$ \Rightarrow {\text{EC}} = 4cm$

${\text{DE}} + {\text{EC}} = {\text{DC}}$

$\Rightarrow {\text{DC}} = 4 + 4 = 8\;{\text{cm}}$

Since, \[{\text{ABCD}}\] is a parallelogram,

${\text{AB}} = {\text{DC}} = 8\;{\text{cm}}$

Now, applied Pythagoras theorem in triangle \[{\text{AED}}\]

$ \Rightarrow {\text{A}}{{\text{D}}^{\text{2}}}{\text{ = A}}{{\text{E}}^{\text{2}}}{\text{ + E}}{{\text{D}}^{\text{2}}}$

$ \Rightarrow {\operatorname{AD} ^2} = {3^2} + {4^2}$

$ \Rightarrow {\text{A}}{{\text{D}}^{\text{2}}}{\text{ = 25}}$

$ \Rightarrow {\text{AD = 5cm}}$

Thus, ${\text{AD}} = {\text{BD}} = 5\;{\text{cm}}$

Perimeter of parallelogram \[{\text{ABCD}}\] $ = 2(l + b)$

$ = 2({\text{DC + AD}}) = 2(8 + 5)$ $ = 2 \times 13 = 26\;{\text{cm}}$

Area of parallelogram \[{\text{ABCD}}\] $ = {{DC \times AE}} = 8 \times 3 = 24\;{\text{c}}{{\text{m}}^2}$.

103. Ishika has designed a small oval race track for her remote control car. Her design is shown in the figure 9.55. What is the total distance around the track? Round your answer to the nearest whole cm.

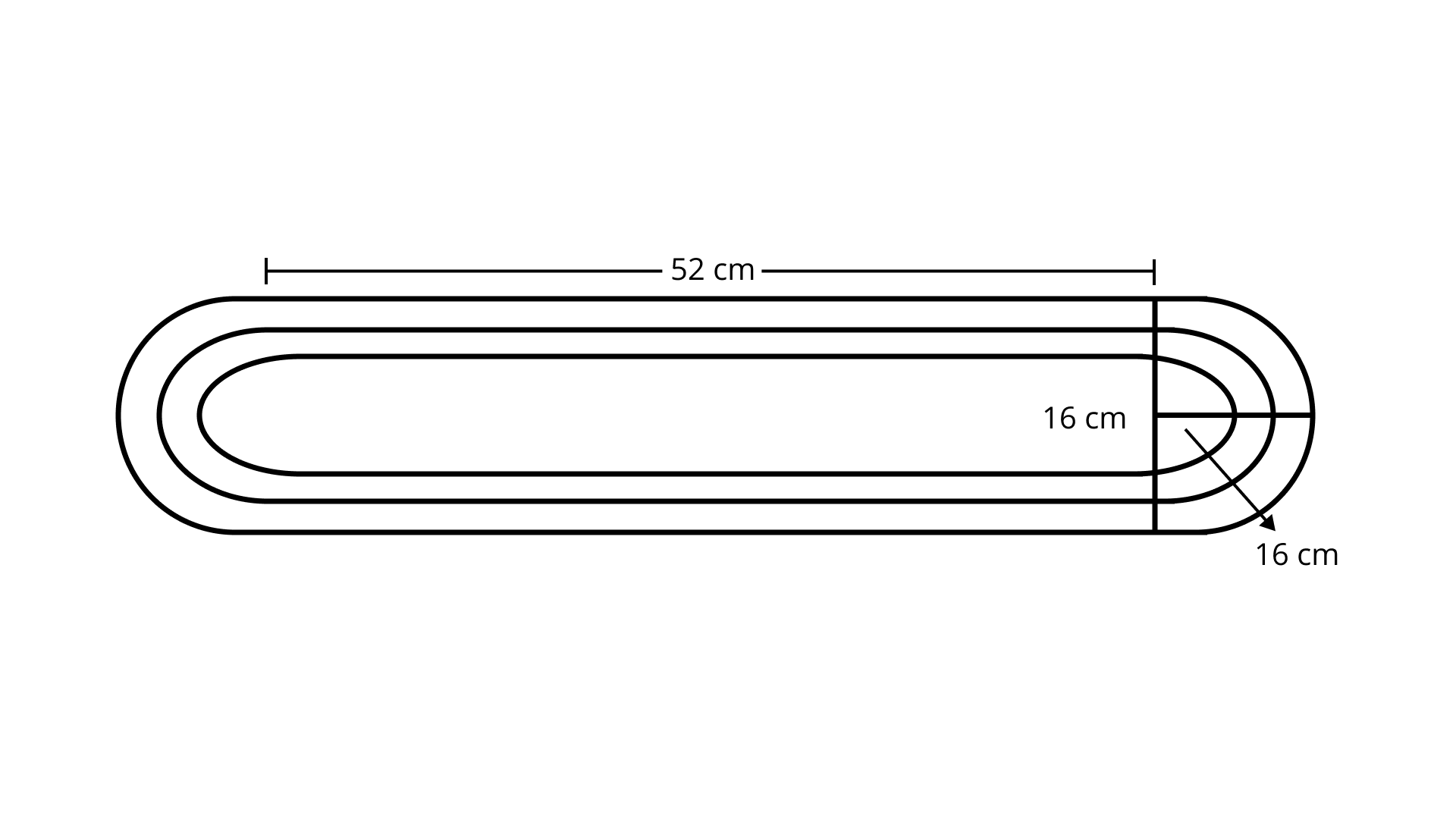
Ans: Total distance around the track $=$ Length of two semicircles $+$ Length of two parallel strips

$ = 2 \times \pi  \times 16 + 2 \times 52$

$ = 2 \times 3.14 \times 16 + 104$

$ = 101 + 104$

$ = 205\;{\text{cm}}$

104. A table cover of dimensions \[{\mathbf{3 m 25 cm  \times  2 m 30 cm}}\] is spread on a table. If \[{\mathbf{30 cm}}\] of the table cover is hanging all around the table, find the area of the table cover which is hanging outside the top of the table. Also find the cost of polishing the table top at Rs. \[{\mathbf{16}}\] per square metre.

Ans:

To find the cost of polishing the table top, we have to find out its area,

Given,

Length of cover $ = 3.25\;{\text{m}}$

Breadth of cover $ = 2.30\;{\text{m}}$

Now, area of the table cover $ = 3.25 \times 2.30 = 7.475\;{{\text{m}}^2}$

Given, $30\;{\text{cm}}$ width of cloth is outside the table an each side.

Hence, length of table $ = 3.25 - 2 \times 30 = 2.65\;{\text{m}}$

Breadth of table $ = 2.30 - 2 \times 30 = 1.70\;{\text{m}}$

Now, area of the top of the table

$ = 2.65 \times 1.70\;{\text{m}} = 4.505\;{{\text{m}}^2}$

Now,

Area of hanging cover of table $ = $  Area of cover of table $ - $ area of the top of the table

$ = 7.475 - 4.505 = 2.97\;{{\text{m}}^2}$

It has been given that Rs.$16$ per square metre is the cost

of polishing the table.

$ = 4.505 \times 16 = Rs.72.08$

105. The dimensions of a plot are ${\mathbf{200\;m \times 150\;m}}$. A builder builds \[{\mathbf{3}}\] roads which are ${\mathbf{3\;m}}$ wide along the length on either side and one in the middle. On either side of the middle road he builds houses to sell. How much area did he get for building the houses?

Ans:

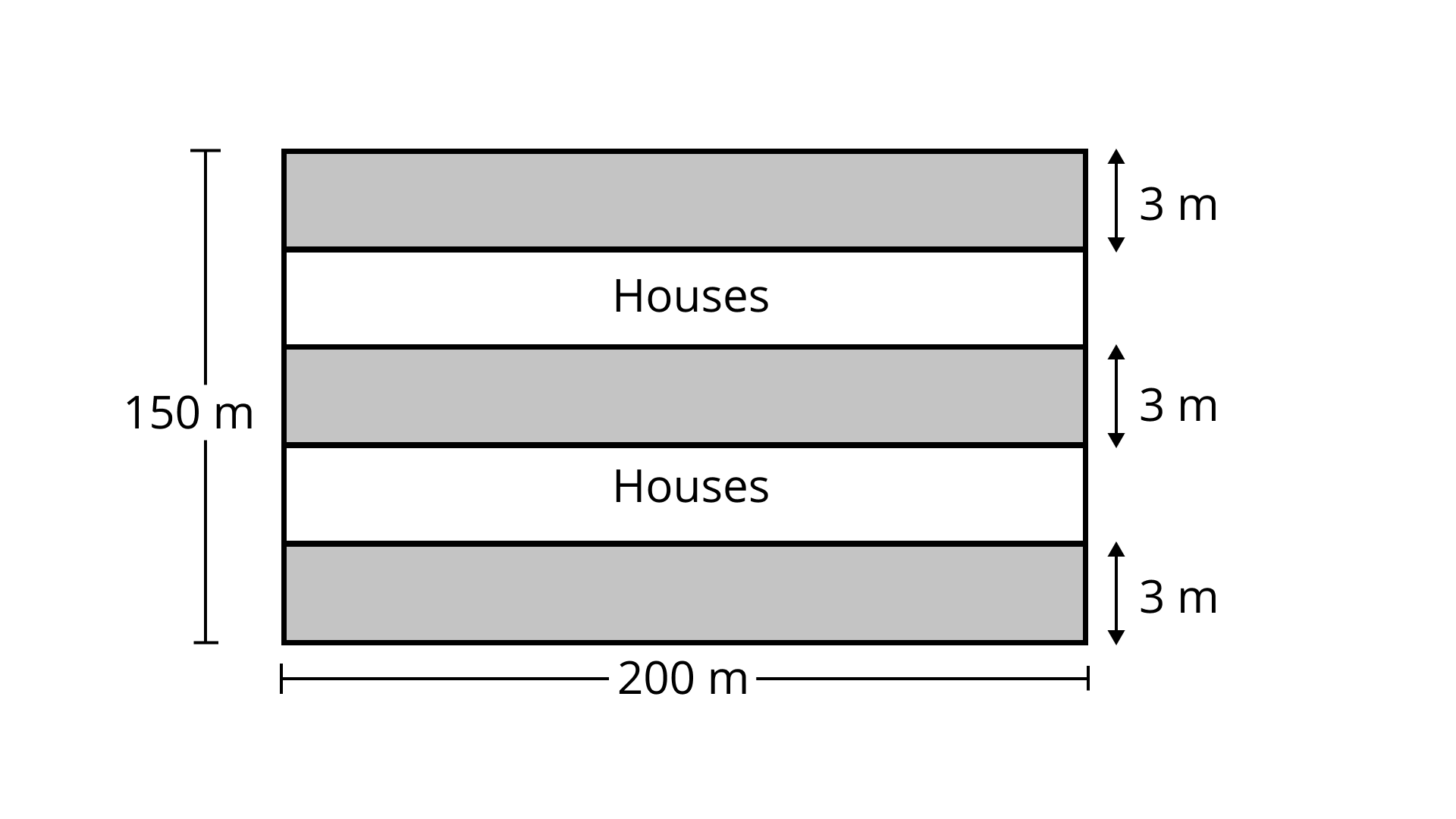
Given,

Dimension of plot $ = (200 \times 150){\text{m}}$

Width of road $ = 3\;{\text{m}}$

Total area required for houses $ = $ Area of total plot $ - $ Area of three roads

$ = 200 \times 150 - 3(3 \times 200)$

$ = 30000 - 1800 = 28200\;{{\text{m}}^2}$

106. A room is ${\mathbf{4}}{\mathbf{.5\;m}}$ long and ${\mathbf{4\;m}}$ wide. The floor of the room is to be covered with tiles of size ${\mathbf{15\;cm}}$ by ${\mathbf{10\;cm}}$. Find the cost of covering the floor with tiles at the rate of \[{\mathbf{4}}{\mathbf{.50}}\] per tile.

Ans: Given that,

Length of room $ = 4.5\;{\text{m}}$

Size of tiles $ = (15 \times 10){\text{cm}}$

Width of room $ = 4\;{\text{m}}$

Area of room $ = 4.5 \times 4 = 18\;{{\text{m}}^2} = 180000\;{\text{c}}{{\text{m}}^2}$

Area of one tile $ = 15 \times 10 = 150\;{\text{c}}{{\text{m}}^2}$

Number of tiles = $\dfrac{\text{Area of room}}{\text{Area of 1 tile}} = \dfrac{{180000}}{{150}} = 1200$

Therefore, cost of covering the floor with tiles $ = 4.50 \times 1200 = $\[Rs.{\text{ }}5400\]

107. Find the total cost of wooden fencing around a circular garden of diameter ${\mathbf{28\;m}}$, if ${\mathbf{1\;m}}$ of fencing costs Rs.\[{\mathbf{300}}\].

Ans: Given,

Diameter of circular garden $ = 28\;{\text{m}}$

Length of the fencing $ = $ circumference of circle $ = \pi d = \dfrac{{22}}{7} \times 28 = 88\;{\text{m}}$

Total cost of fencing $ = 88 \times 300 = Rs.26400$

108. Priyanka took a wire and bent it to form a circle of radius ${\mathbf{14\;cm}}$. Then she bent it into a rectangle with one side ${\mathbf{24\;cm}}$ long. What is the length of the wire? Which figure encloses more area, the circle or the rectangle?

Ans: Given that,

Radius of circle $ = 14\;{\text{cm}}$

Length of rectangle $ = 24\;{\text{cm}}$

Hence, length of the wire $ = $ circumference of circle $ = 2\pi r = 2 \times \dfrac{{22}}{7} \times 14 = 88m$

Let $b$ be the width of a rectangle.

Since, the wire is rebent in the form of rectangle

Hence, perimeter of rectangle $ = $ circumference of circle

$ \Rightarrow 2(24 + b) = 88$

$ \Rightarrow 24 + b = 44$

$ \Rightarrow b = 44 - 24$

$ \Rightarrow b = 20\;{\text{cm}}$

${\text{Area of circle }} = \pi {r^2} = \dfrac{{22}}{7} \times 14 \times 14 = 616\;{\text{c}}{{\text{m}}^2}$

Area of rectangle $ = 24 \times 20 = 480\;{\text{c}}{{\text{m}}^2}$

Therefore, the circle encloses more area than the rectangle.

109. How much distance, in metres, a wheel of ${\mathbf{25\;cm}}$ radius will cover if it rotates \[{\mathbf{350}}\] times?

Ans: Given that,

Radius of wheel $ = 25\;{\text{cm}} = \dfrac{1}{4}{\text{m}}$ 

Distance travelled in one rotation

$ = 2\pi r = 2 \times \dfrac{{22}}{7} \times \dfrac{1}{4}$

$ = \dfrac{{11}}{7}m$

Distance travelled in $350$ rotations

$ = \dfrac{{11}}{7} \times 350 = 550\;{\text{m}}$

Therefore, the wheel covers $550\;{\text{m}}$ distance.

110. A circular pond is surrounded by a ${\mathbf{2\;m}}$ wide circular path. If the outer circumference of the circular path is ${\mathbf{44\;m}}$, find the inner circumference of the circular path. Also find the area of the path.

Ans:

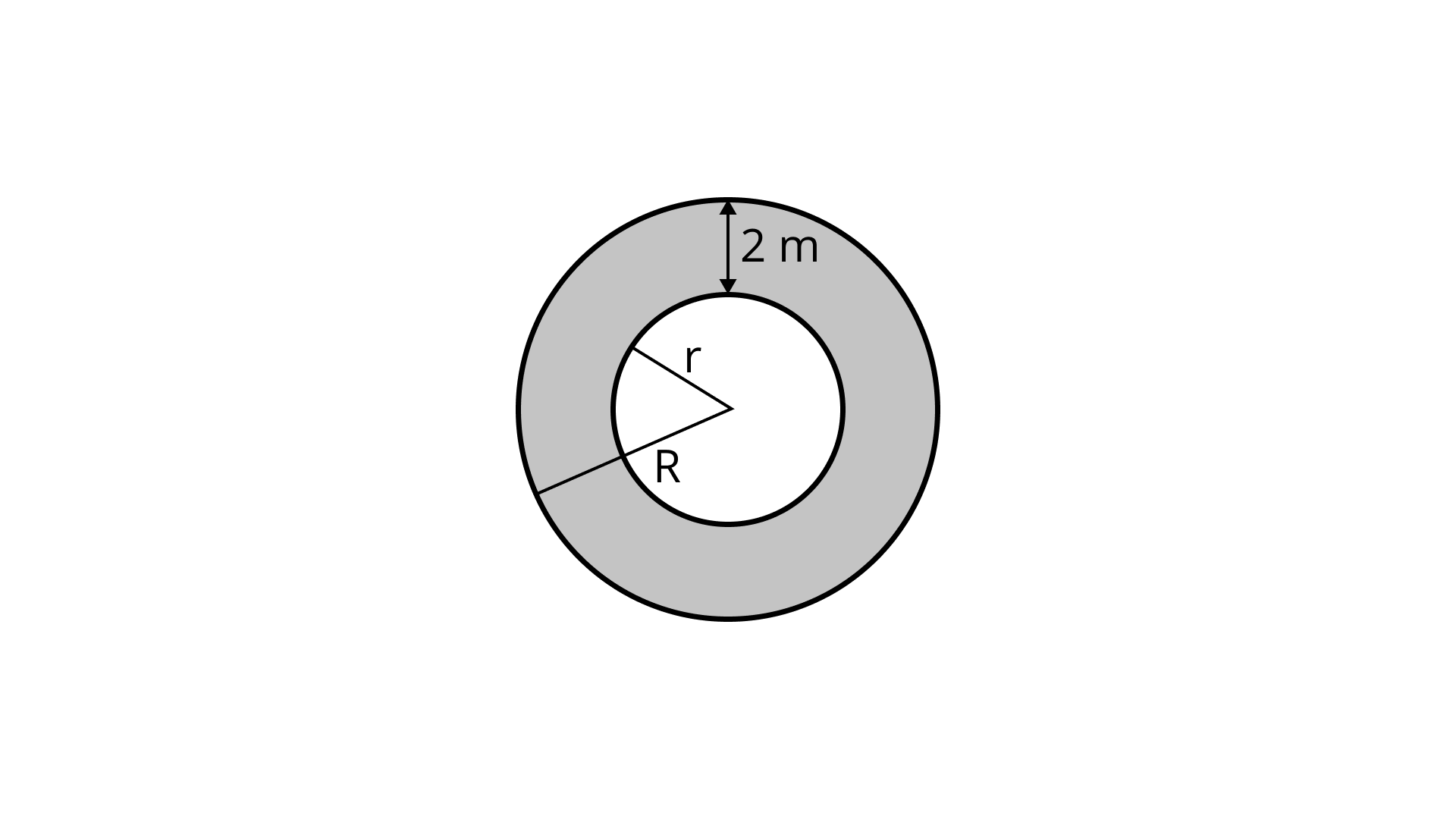
Let $R$ be radius of outer circle and $r$ be radius of inner circle,

It has been given that $44\;{\text{m}}$ is the circumference of outer circle,

$ \Rightarrow 2\pi R = 44m$

$ \Rightarrow 2\times \dfrac{22}{7} R = 44m$

$ \Rightarrow R = 7 m$

Since, $r = (R - 2) = (7 - 2)m = 5m$

$ = 2\pi r = 2 \times \dfrac{{22}}{7} \times 5$

$ = 31.43\;{\text{m}}$

Therefore, area of the path $ = $ area of outer circle $ - $ area of inner circle 

$= \pi \left( {{R^2} - {r^2}} \right)$

$ = \dfrac{{22}}{7}\left( {{7^2} - {5^2}} \right) = \dfrac{{22}}{7} \times 24$

$ = 75.43{m^2}$

111. A carpet of size ${\mathbf{5\;m \times 2\;m}}$ has ${\mathbf{25\;cm}}$ wide red border. The inner part of the carpet is blue in color (Fig.) Find the area of the blue portion. What is the ratio of areas of red portion to blue portion?

Ans:

Given that,

Size of carpet $ = 5 \times 2\;{\text{m}}$

Width of border $ = 25\;{\text{cm}} = 0.25\;{\text{m}}$

Area of carpet ${\text{ABCD}} = {{AB \times BC}} = 5 \times 2 = 10\;{{\text{m}}^2}$

Thus, length of inner blue portion,

${\text{EF}} = {\text{AB}} - (2 \times 0.25\;{\text{cm}}) = 5 - 0.50 = 4.5\;{\text{m}}$

Breadth of inner blue portion

${\text{FG = BC}} - (2 \times 0.25) = 2 - 0.50 = 1.5{\text{m}}$

Area of blue portion $ = $ area of rectangle \[{\text{EFGH}}\]

${{ = EF \times FG}} = 4.5 \times 1.5 = 6.75\;{{\text{m}}^2}$

Now,

Area of red portion $ = $ area of rectangle ${\text{ABCD}}$ $ - $ area of rectangle \[{\text{EFGH}}\]

$ = 10 - 6.75 = 3.25\;{{\text{m}}^2}$

Therefore, the ratio of area of red and blue portions $ = 3.25:6.75 = 13:27$

112. Use the Fig. 9.57 showing the layout of a farmhouse:

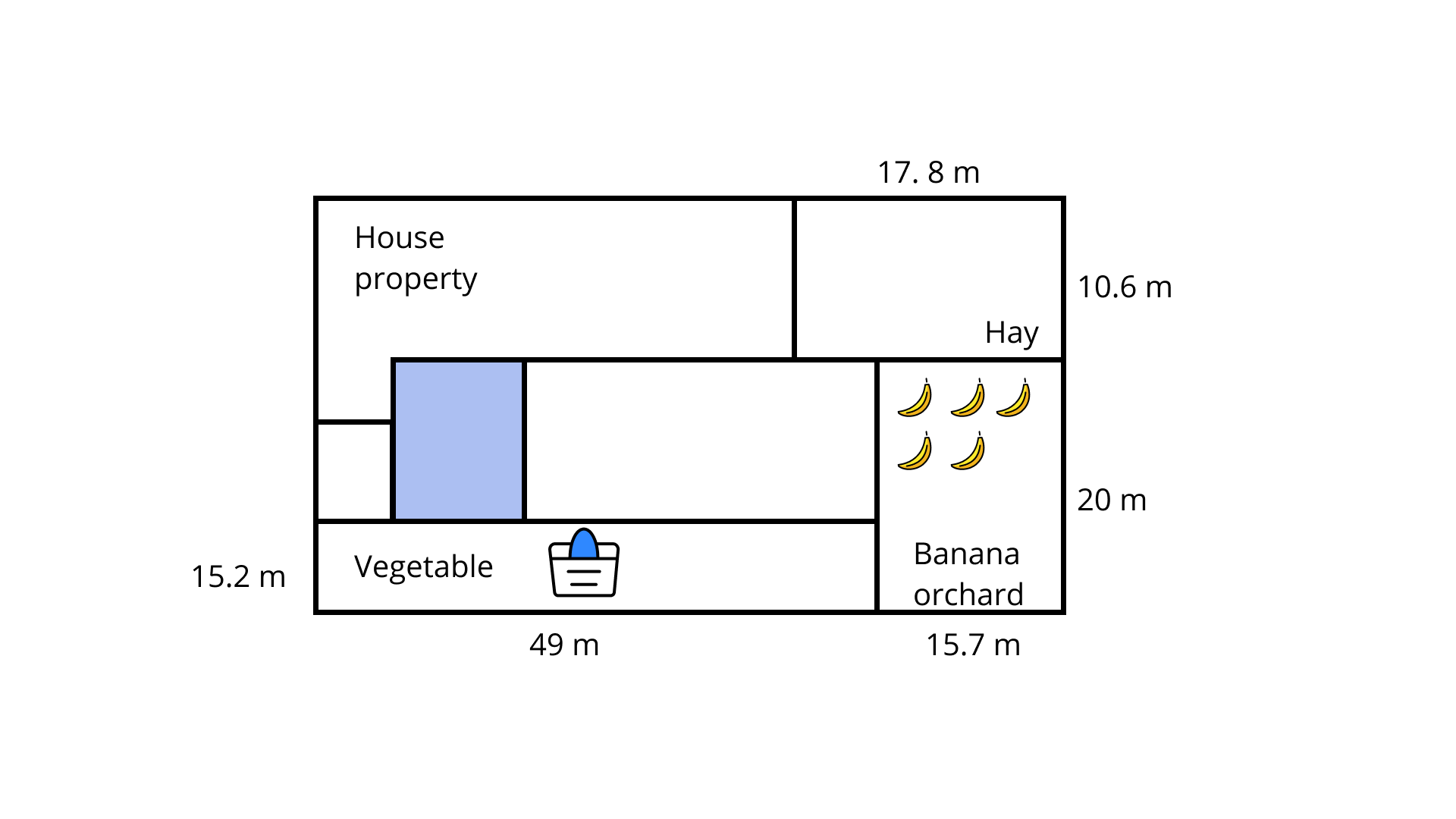
(a) What is the area of land used to grow hay?

Ans: Area of land used to grow hay

$ = 17.8 \times 10.6 = 188.68\;{{\text{m}}^2}$

(b) It costs ₹ \[{\mathbf{91}}\] per ${{\mathbf{m}}^{\mathbf{2}}}$ to fertilise the vegetable garden. What is the total cost?

Ans: Area of vegetable garden $ = 49 \times 15.2 = 744.80\;{{\text{m}}^2}$

Since, cost to fertilise $1\;{{\text{m}}^2}$ vegetable garden $ = $ Rs.\[91\]

Hence, cost to fertilise $744.8 {{\text{m}}^2}$ vegetable garden $ = 91 \times 744.80 = $ Rs. $67776.80$

(c) A fence is to be enclosed around the house. The dimensions of the house are ${\mathbf{18}}{\mathbf{.7\;m \times 12}}{\mathbf{.6\;m}}$. At least how many metres of fencing are needed?

Ans: Fence is of dimension $(18.7 \times 12.6)m$ around the house.

Perimeter of the house $ = 2(l + b)$

Hence, total lengths of the fence $ = 2(18.7 + 12.6) = 2 \times 31.3 = 62.6\;{\text{m}}$

(d) Each banana tree required ${\mathbf{1}}{\mathbf{.25\;}}{{\mathbf{m}}^{\mathbf{2}}}$ of ground space. How many banana trees can there be in the orchard?

Ans: Area covered by banana orchard = $(20 \times 15.7)m = 314{m^2}$

Since, \[1.25{\text{ }}sq.\] area required by $1$ banana tree. Hence, number of bananas required to fill area of $314 {{\text{m}}^2}$

$ = \dfrac{{314}}{{1.25}} = 251.25 \approx 251$ trees

113. Study the layout given below in Fig. 9.58 and answer the questions:

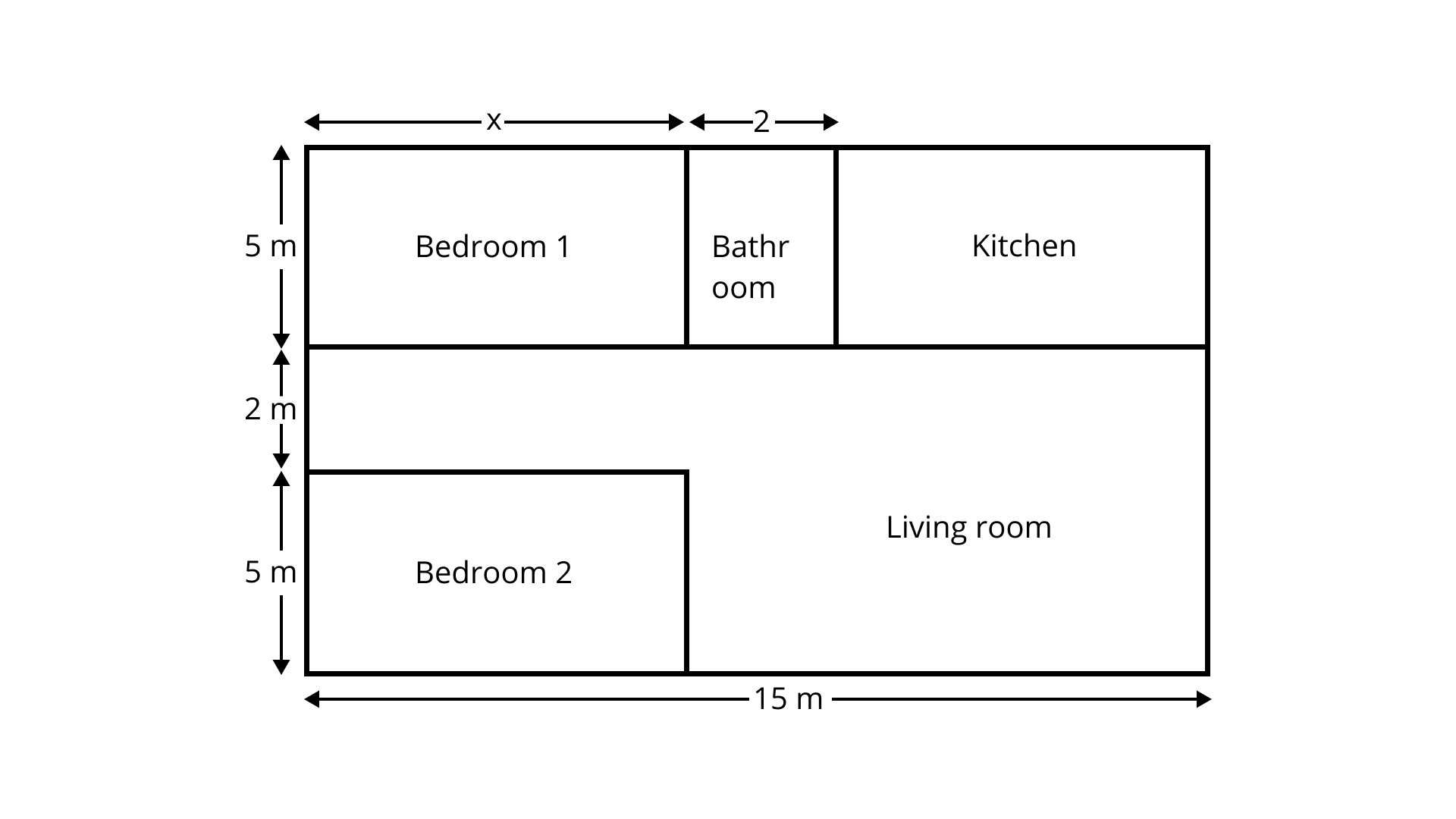
(a) Write an expression for the total area covered by both the bedrooms and the kitchen.

Ans: Area of both kitchen and bedrooms $ = 2$ times of area of bedroom $ + $area of kitchen

$ = 2(5 \times x) + [15 - (x + 2)] \times 5$

$ = 10x + (75 - 5x - 10)$

$ = 10x + 65 - 5x$

$ = (65 + 5x){m^2}$

(b) Write an expression to calculate the perimeter of the living room.

Ans: Perimeter of the living room

$ = 15 + 2 + 5 + (15 - x) + 5 + x + 2 = 44m$

(c) If the cost of carpeting is Rs. ${\mathbf{50/}}{{\mathbf{m}}^{\mathbf{2}}}$, write an expression for calculating the total cost of carpeting both the bedrooms and the living room.

Ans: Total area of both living the room and the bedrooms $ = 5 \times x + 7 \times 15 = (5x + 105){m^2}$

Therefore, total cost of carpeting $ = (5x + 105) = $ Rs. $250(x + 21)$

(d) If the cost of tiling is Rs. ${\mathbf{30/}}{{\mathbf{m}}^{\mathbf{2}}}$, write an expression for calculating the total cost of floor tiles used for the bathroom and kitchen floors.

Ans: Total area of bathroom and kitchen $ = (15 - x) \times 5{m^2}$

Therefore, total cost of tilling $ = (15 - x) \times 5 \times 30 = Rs.150(15 - x)$

(e) If the floor area of each bedroom is ${\mathbf{35\;}}{{\mathbf{m}}^{\mathbf{2}}}$, Then find ${\mathbf{x}}$.

Ans: Given,

Area of floor of each bedroom $ = 35{\text{Sqm}}$ 

Area of one bedroom $ = 5x$$Sq.m$ 

$\therefore 5x = 35$

$ \Rightarrow x = 7m$

114. A ${\mathbf{10}}\;{\mathbf{m}}$ long and ${\mathbf{4}}\;{\mathbf{m}}$ wide rectangular lawn is in front of a house. Along its three sides, a ${\mathbf{50\;cm}}$ wide flowerbed is there as shown in Fig. 9.58. Find the area of the remaining portion.

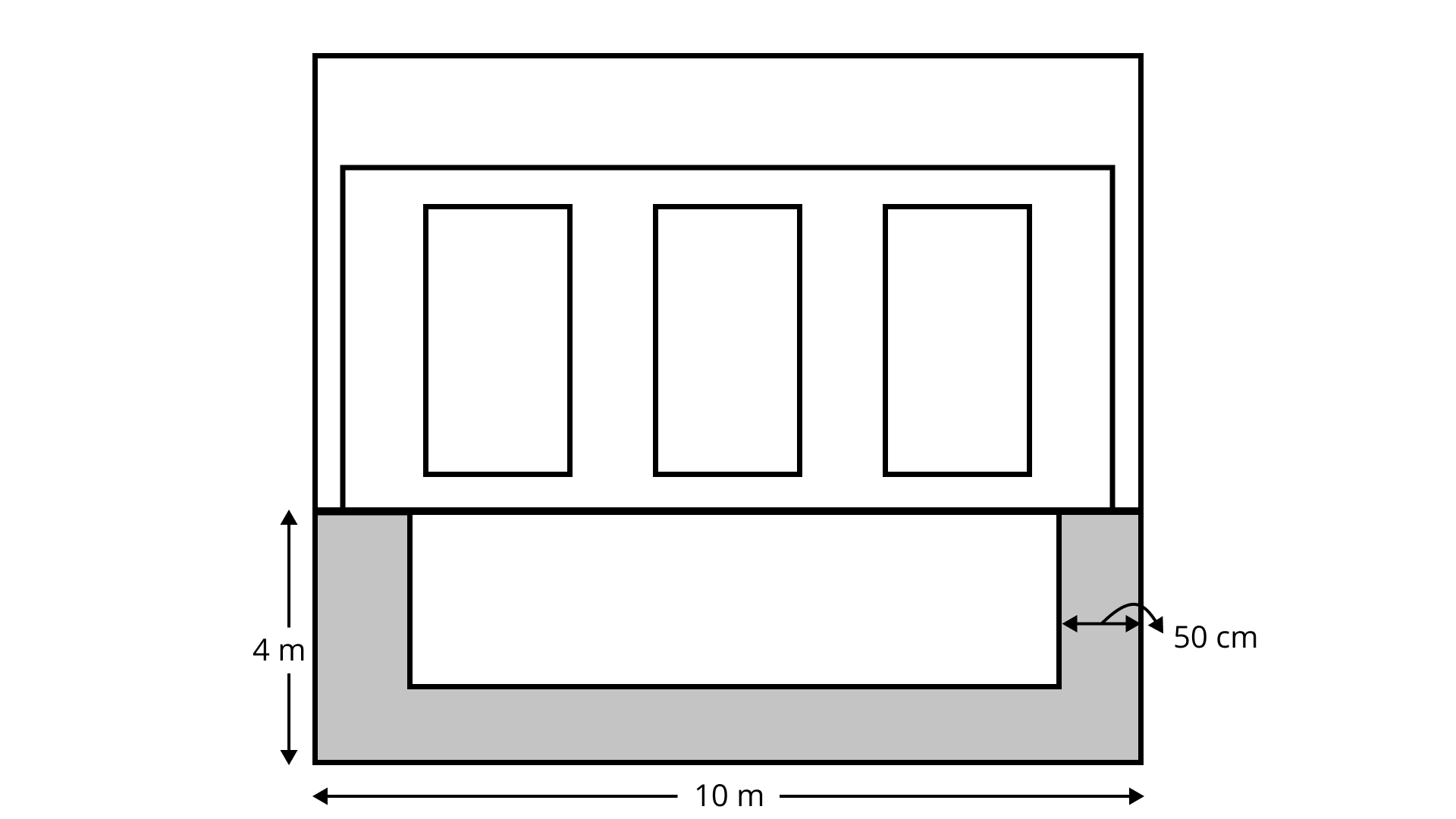
Ans:

Given that,

Dimension of rectangular lawn $ = (10 \times 4){\text{m}}$

Width of flowerbed $ = 50\;{\text{cm}}$

Length of remaining portion

${\text{EF = AB}} - (50 \times 2\;{\text{cm}})$

$ = 10m - 100 = 10 - 1 = 9m$

Breadth of remaining region,

${\text{EH = AD}} - 50\;{\text{cm}} = 4 - 0.5 = 3.5\;{\text{m}}$

Therefore, required area $ = $ area of \[{\text{EFGH}}\]

${{ = EF \times EH}} = 9 \times 3.5 = 31.5\;{{\text{m}}^2}$

115. A school playground is divided by a ${\mathbf{2\;m}}$ wide path which is parallel to the width of the playground, and a ${\mathbf{3\;m}}$ wide path which is parallel to the length of the ground (Fig. 9.60). If the length and width of the playground are ${\mathbf{120\;m}}$ and ${\mathbf{80\;m}}$ respectively, find the area of the remaining playground.

Ans:

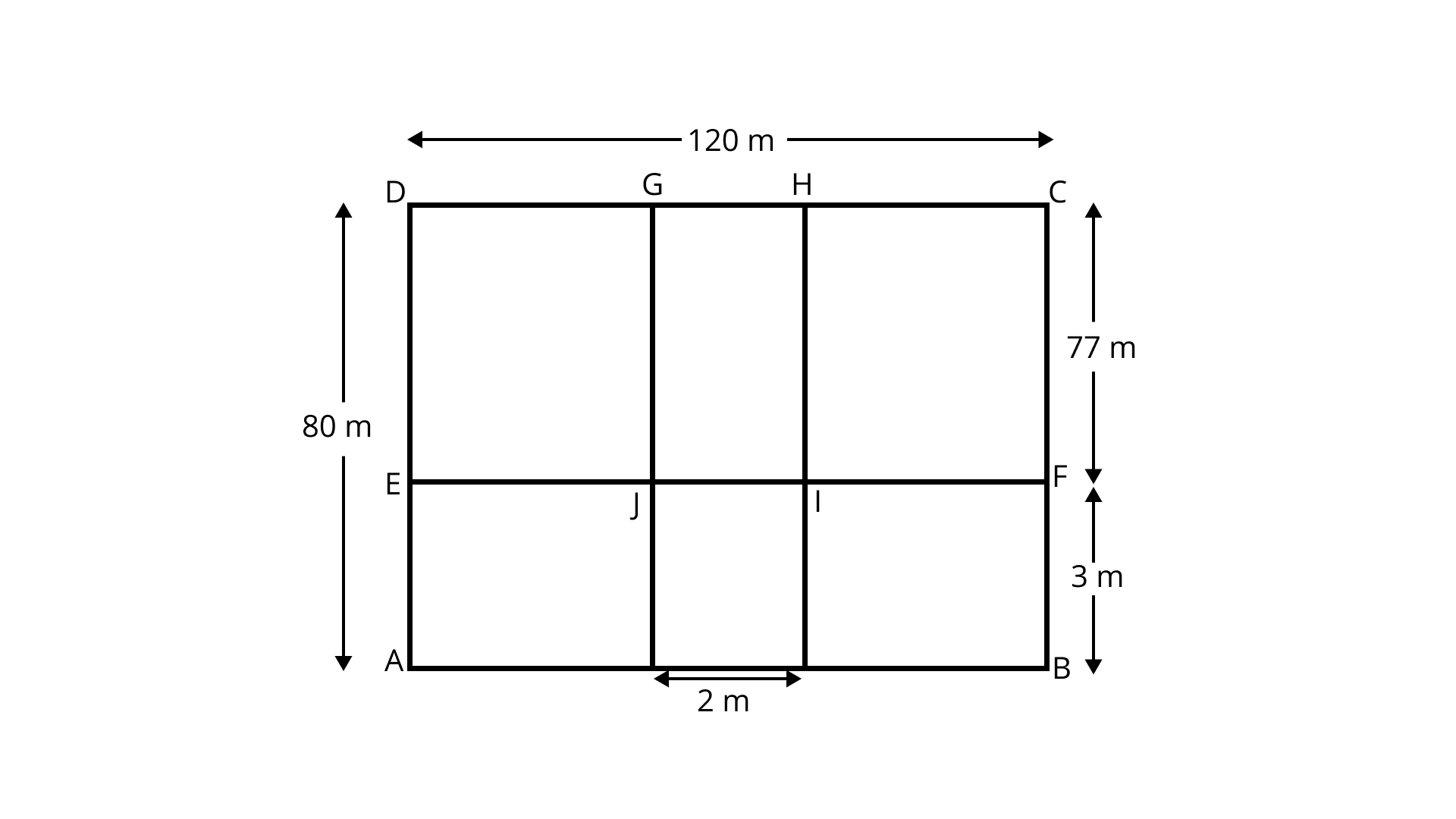
Given that,

Dimension of playground $ = (120 \times 80){\text{m}}$

Area of rectangle ${\text{ABCD}} = 120 \times 80 = 9600\;{{\text{m}}^2}$

Area of rectangle \[{\text{ABFE}}\]

${{ = AB \times BF}} = 120 \times 3 = 360\;{{\text{m}}^2}$

Area of rectangle \[{\text{GHIJ}}\]

${{ = JI \times IH = 2 \times 77 = 154\;}}{{\text{m}}^{\text{2}}}$

Area of Remaining ground rectangle $ = $Area of rectangle ${\text{ABCD}}\, - $ Area of rectangle ${\text{ABFE}} - $Area of rectangle \[GHIJ\]

$ = 9600 - 360 - 154 = 9086{m^2}$

116. In a park of dimensions ${\mathbf{20\;m \times 15\;m}}$, there is a ${\mathbf{L}}$ shaped ${\mathbf{1\;m}}$ wide flower bed as shown in Fig. 9.61. Find the total cost of manuring for the flower bed at the rate of Rs ${\mathbf{45 per}}{{\mathbf{m}}^{\mathbf{2}}}$.

Ans: 

Given,

Dimensions of a given park $ = (20 \times 15){\text{m}}$

Width of flowerbed $ = 1\;{\text{m}}$

From the figure,

$FG = BC - 1m = (15 - 1) = 14m$

$EF = DC - 1 = 20 - 1 = 19m$ 

Therefore, area of flower bed = Area of rectangle ${\text{ABCD}} - $Area of rectangle EFGD

$ = 20 \times 15 - 19 \times 14 = 300 - 266 = 34{m^2}$

Rs. \[45\] is the cost for manuring 1 square metre of flower bed.

Therefore, the cost of manuring of \[34\] square metres of flowerbed.

$ = 34 \times 45 = Rs.1530$

117. Dimensions of a painting are ${\mathbf{60\;cm \times 38\;cm}}$. Find the area of the wooden frame of width ${\mathbf{6\;cm}}$ around the painting as shown in Fig.

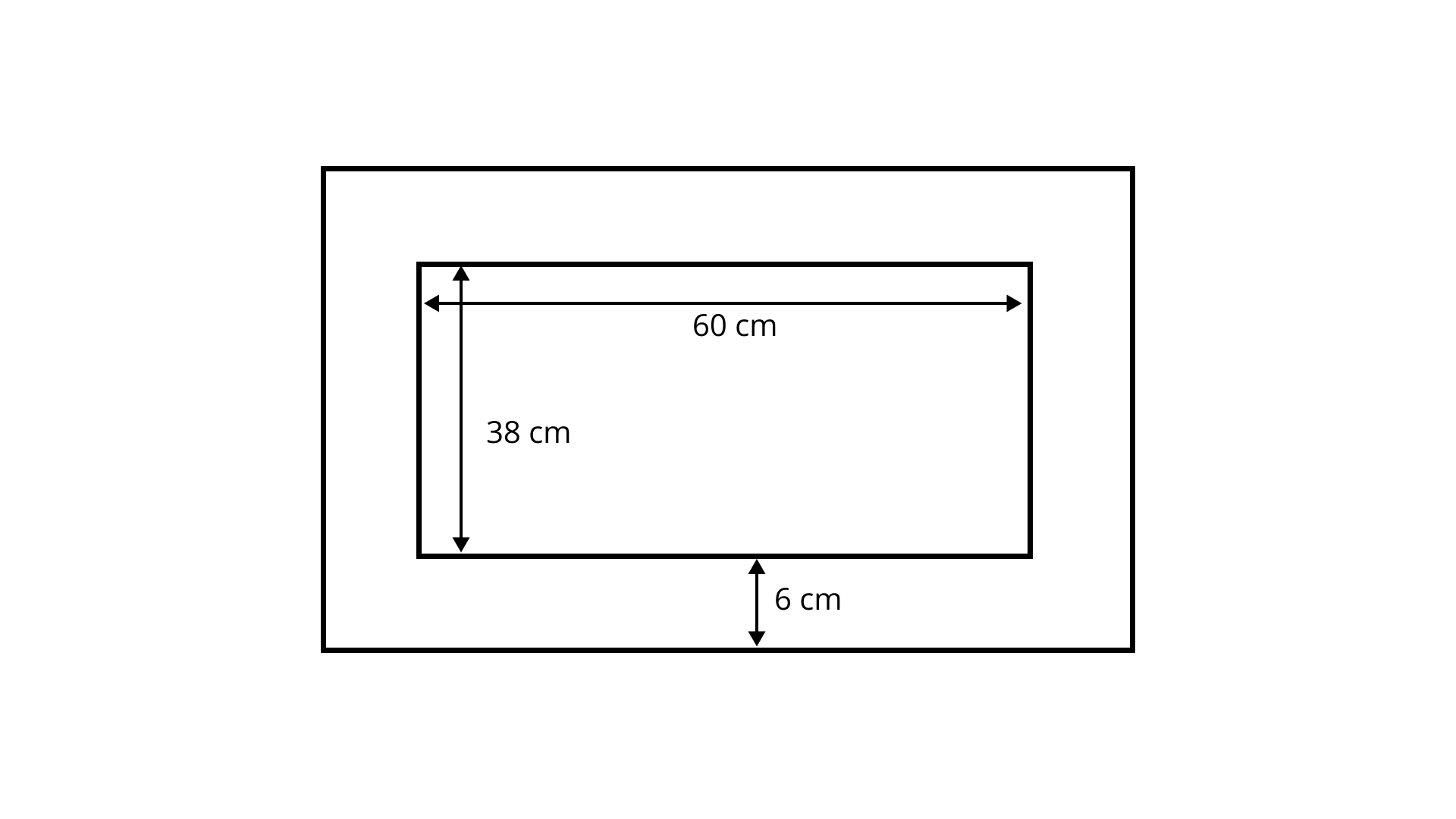
Ans: Given,

Length of inner rectangle $ = 60\;{\text{cm}}$

Breadth of inner rectangle $ = 38\;{\text{cm}}$

Thus, area of inner rectangle

$ = 60 \times 38 = 2280\;{\text{c}}{{\text{m}}^2}$

Length of outer rectangle $ = 38 + 6 + 6 = 50\;{\text{cm}}$

Breadth of outer rectangle $ = 60 + 6 + 6 = 72\;{\text{cm}}$

Thus, area of outer rectangle

$ = 50 \times 72 = 3600\;{\text{c}}{{\text{m}}^2}$

Now,

Area of wooden frame $ = 3600 - 2280 = 1320\;{\text{c}}{{\text{m}}^2}$

118. A design is made up of four congruent right triangles as shown in Fig. 9.63. Find the area of the shaded portion.

Ans: Area of one right-angled triangle $ = \dfrac{1}{2} \times BA \times BG = \dfrac{1}{2} \times 10 \times 30 = 150\;{\text{c}}{{\text{m}}^2}$

Thus, area of 4 right-angled triangles $ = 4 \times 150 = 600\;{\text{c}}{{\text{m}}^2}$

Area of portion ${\text{ABCD}} = {(30 + 10)^2} = 1600\;{\text{c}}{{\text{m}}^2}$

Therefore, area of shaded portion $ = 1600 - 600 = 1000\;{\text{c}}{{\text{m}}^2}$

119. A square tile of length ${\mathbf{20\;cm}}$ has four quarter circles at each corner as shown in Fig. 9.64(i). Find the area of the shaded portion. Another tile with the same dimensions has a circle in the centre of the tile [Fig. 9.64 (ii)]. If the circle touches all the four sides of the square tile, find the area of the shaded portion. In which tile, the area of the shaded portion will be more? (Take${\mathbf{\pi  = 3}}{\mathbf{.14}}$)

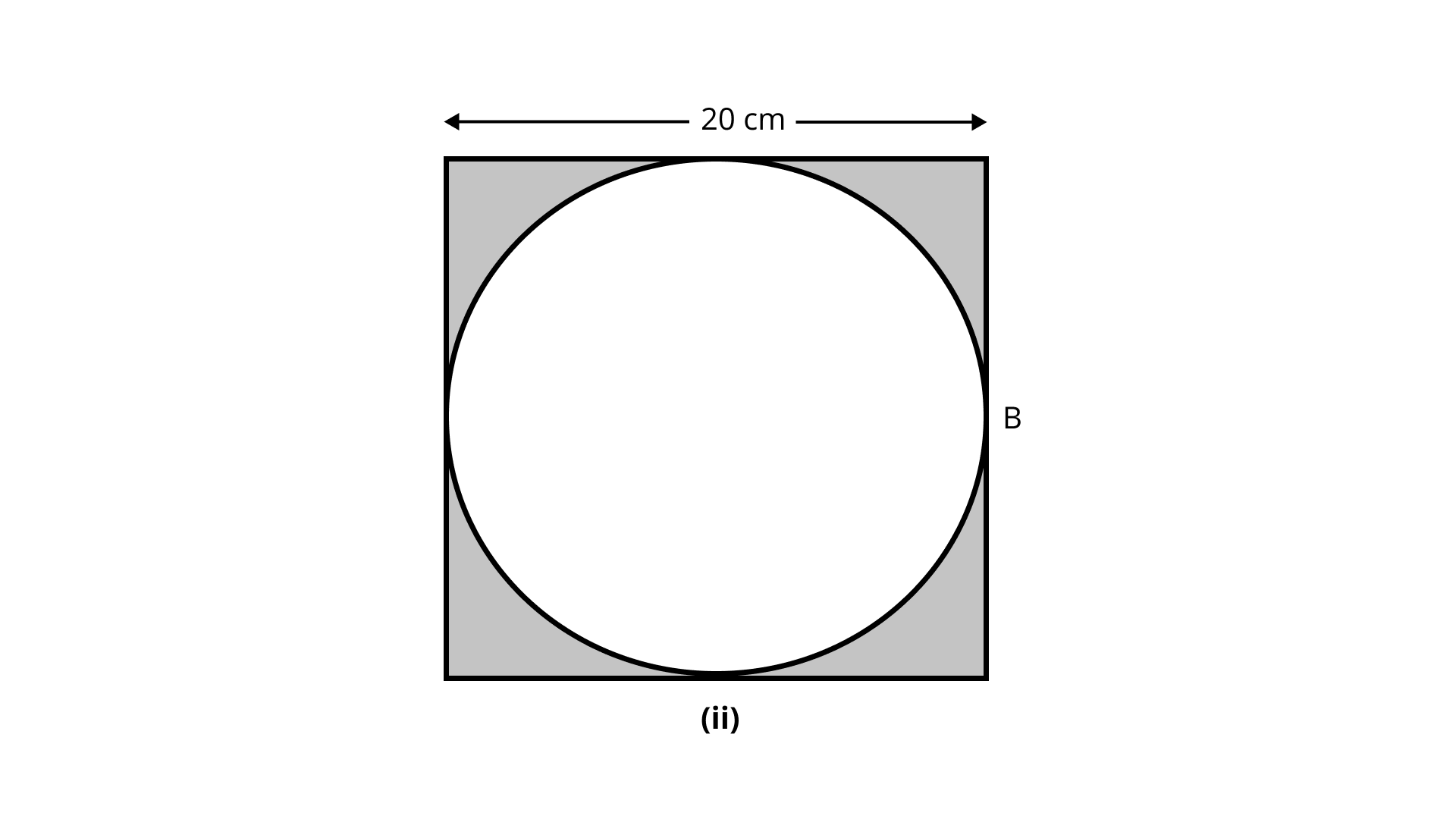
Ans: Figure 1 

Area of shaded portion \[ = \] Area of square \[ - 4\]times of Area of quarter circle

$ = 20 \times 20 - 4 \times \dfrac{{\pi {r^2}}}{4}$

$ = 400 - 4 \times \dfrac{{22}}{7} \times \dfrac{1}{4} \times 10 \times 10$

$ = 400 - \dfrac{{2200}}{7} = \dfrac{{600}}{7}$

$ = 85.71\;{\text{c}}{{\text{m}}^2} = 86\;{\text{c}}{{\text{m}}^2}$

Figure ii

Area of shaded portion =$\text{Area of square}  - \text{Area of circle}$

$ = 20 \times 20 - \pi {r^2}$

$ = 400 - \dfrac{{22}}{7} \times 10 \times 10$

$ = 400 - \dfrac{{2200}}{7}$

$ = \dfrac{{600}}{7}$

$ = 86{\text{c}}{{\text{m}}^2}$

Therefore, both cases have equal areas.

120. A rectangular field is ${\mathbf{48\;m}}$ long and ${\mathbf{12\;m}}$ wide. How many right triangular flower beds can be laid in this field, if sides including the right angle measure ${\mathbf{2\;m}}$ and ${\mathbf{4\;m}}$, respectively?

Ans: Given,

Dimensions of field $ = (48 \times 12){\text{m}}$

Dimension of right-angled triangle $ = (2 \times 4){\text{m}}$

Therefore, number of right-angled triangular flowerbeds

$ = \dfrac{{48 \times 12}}{{\dfrac{1}{2} \times 2 \times 4}}$

$ = 114$

121. Ramesh grew wheat in a rectangular field that measured \[{\mathbf{32}}\] metres long and \[{\mathbf{26}}\]metres wide. This year he increased the area for wheat by increasing the length but not the width. He increased the area of the wheat field by \[{\mathbf{650}}\] square metres. What is the length of the expanded wheat field?

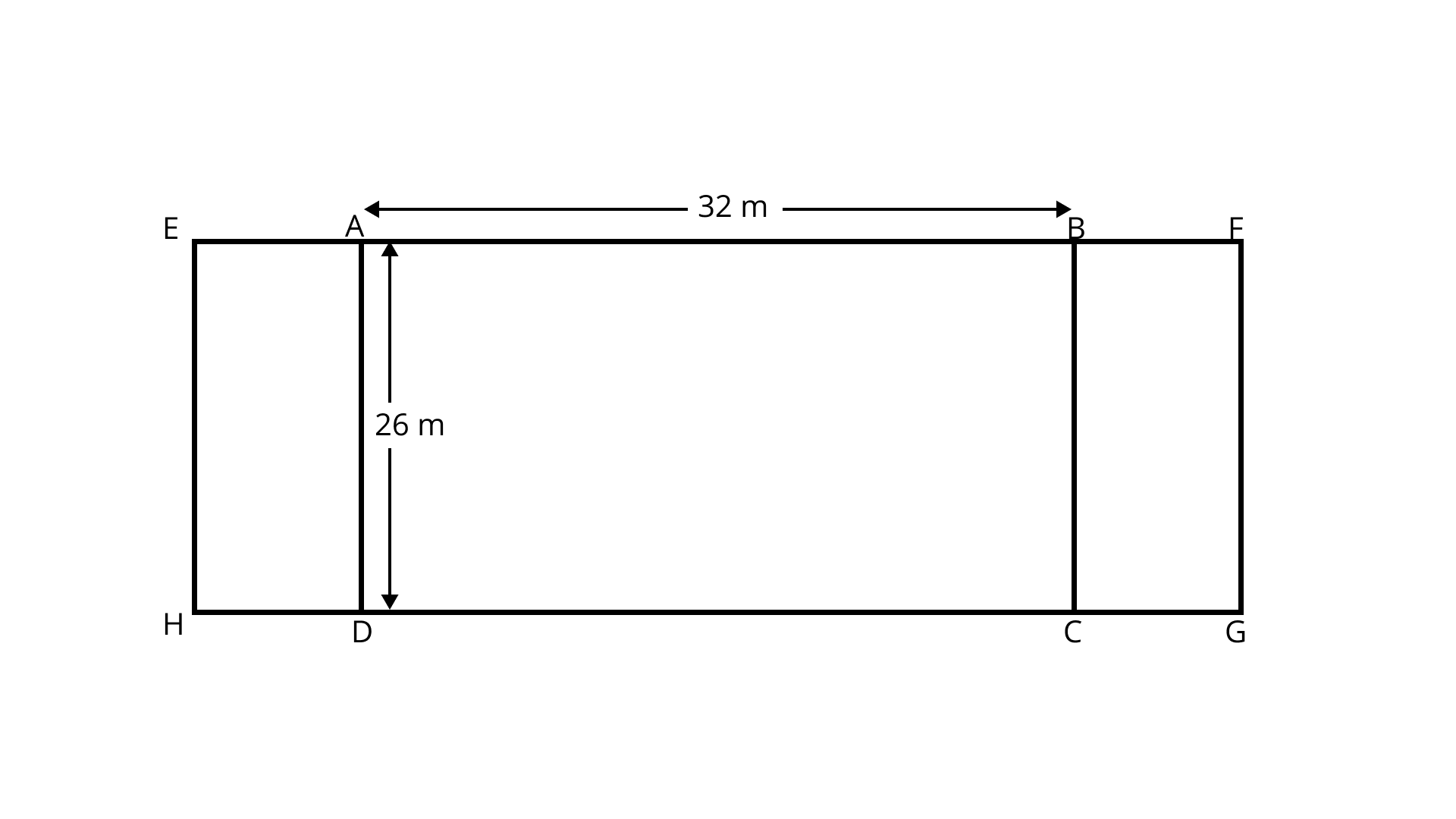
Ans: Given,

Dimensions of field $ = (32 \times 26){\text{m}}$

Increased area $ = 650{\text{Sq}}$ metres

So, increased area of wheat field $ = $ Area of rectangle \[EFGH\]- Area of rectangle ${\text{ABCD}}$(wheat field)

$ \Rightarrow 650 = EF \times EH - AB \times AD$

$ \Rightarrow 650 = EF \times 26 - 32 \times 26$

$ \Rightarrow 650 = 26 \times EF - 832$

$ \Rightarrow EF = 57{\text{m}}$

Therefore, increased length of wheat field is $57m.$

122. In Fig. 9.65, triangle AEC is right-angled at E, B is a point on EC, ${\mathbf{BD}}$ is the altitude of triangle ${\mathbf{ABC,AC = 25\;cm,BC = 7\;cm}}$ and ${\mathbf{AE = 15\;cm}}$. Find the area of the triangle ${\mathbf{ABC}}$ and the length of ${\mathbf{DB}}$.

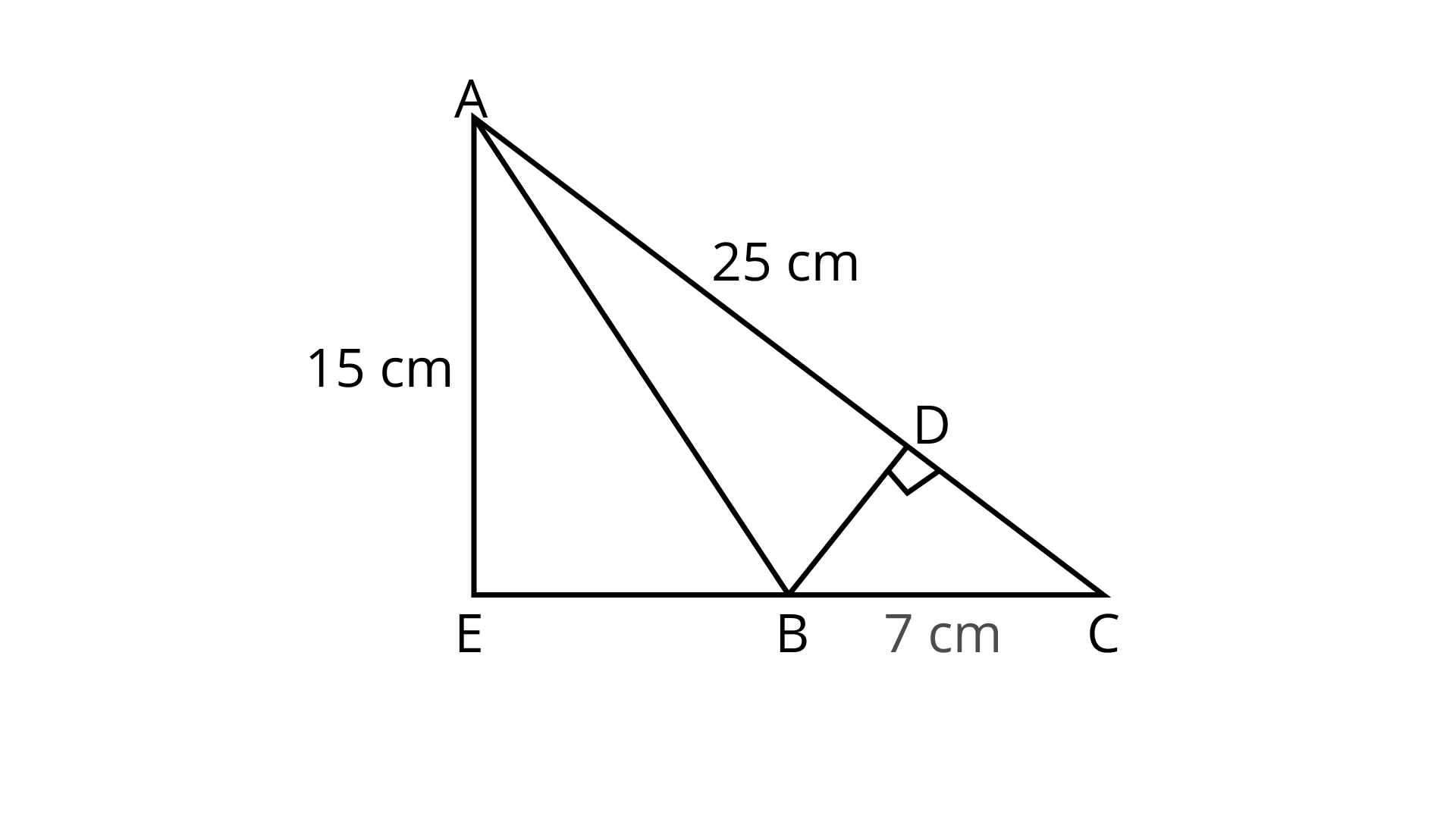
Ans: Given,

${\text{AC}} = 25\;{\text{cm}}$,

${\text{AE}} = 15\;{\text{cm}}$,

${\text{BC}} = 7\;{\text{cm}}$

Applying Pythagoras theorem in triangle ${\text{AEC}}$,

$A{C^2} = A{E^2} + E{C^2}$

$\Rightarrow E{C^2} = {25^2} - {15^2}$

$\Rightarrow E{C^2} = 625 - 225$

$\Rightarrow EC = 20\;{\text{cm}}$

Now, $EB = EC - BC = 20 - 7 = 13\;{\text{cm}}$

Area of triangle AEC,

$ = \dfrac{1}{2} \times AE \times EC$

$ = \dfrac{1}{2} \times 15 \times 20 = 150\;{\text{c}}{{\text{m}}^2}$

Now, Area of triangle AEB,

$ = \dfrac{1}{2} \times AE \times EB$

$ = \dfrac{1}{2} \times 15 \times 13 = 97.5{\text{c}}{{\text{m}}^2}$

Thus, area of triangle ${\text{ABC}} = $ Area of triangle ${\text{AEC}}$ - Area of triangle AEB

$ = 150 - 97.5$

$ = 52.5{\text{c}}{{\text{m}}^2}$

Now, again area of triangle ABC

$ \Rightarrow 52.5 = \dfrac{1}{2} \times BD \times AC$

$\Rightarrow 52.5 = \dfrac{1}{2} \times BD \times 25$

$\Rightarrow BD = \dfrac{{52.5 \times 2}}{{25}} = 4.2\;{\text{cm}}$

Therefore, $52.5$ square centimetres is the area of triangle ${\text{ABC}}$ and length of DB is $4.2\;{\text{cm}}$.

123. 

Ans: Number of pieces of chocolate=

$ = \dfrac{{18 \times 18}}{{1.5 \times 2}}$

$ = \dfrac{{324}}{3}$

$ = 108$

Therefore, the number of pieces of chocolate are $108.$

124. Calculate the area of the shaded region in Fig. 9.66, where all of the short line segments are at right angles to each other and ${\mathbf{1\;cm}}$ long.

Ans: Length of the larger rectangle $ = 1 \times 9\;{\text{cm}} = 9\;{\text{cm}}$

Breadth of the larger rectangle $ = 1 \times 9\;{\text{cm}} = 9\;{\text{cm}}$

Thus, area of shaded portion $ = $ (area of larger square $ - 41$ small identical squares)

$ = 81 - 41$

$ = 40\;{\text{c}}{{\text{m}}^2}$

Thus, the area of the shaded portion is $40\;{\text{c}}{{\text{m}}^2}$.

125. The plan and measurement for a house are given in Fig. 9.67. The house is surrounded by a path \[{\mathbf{1m}}\] wide. 

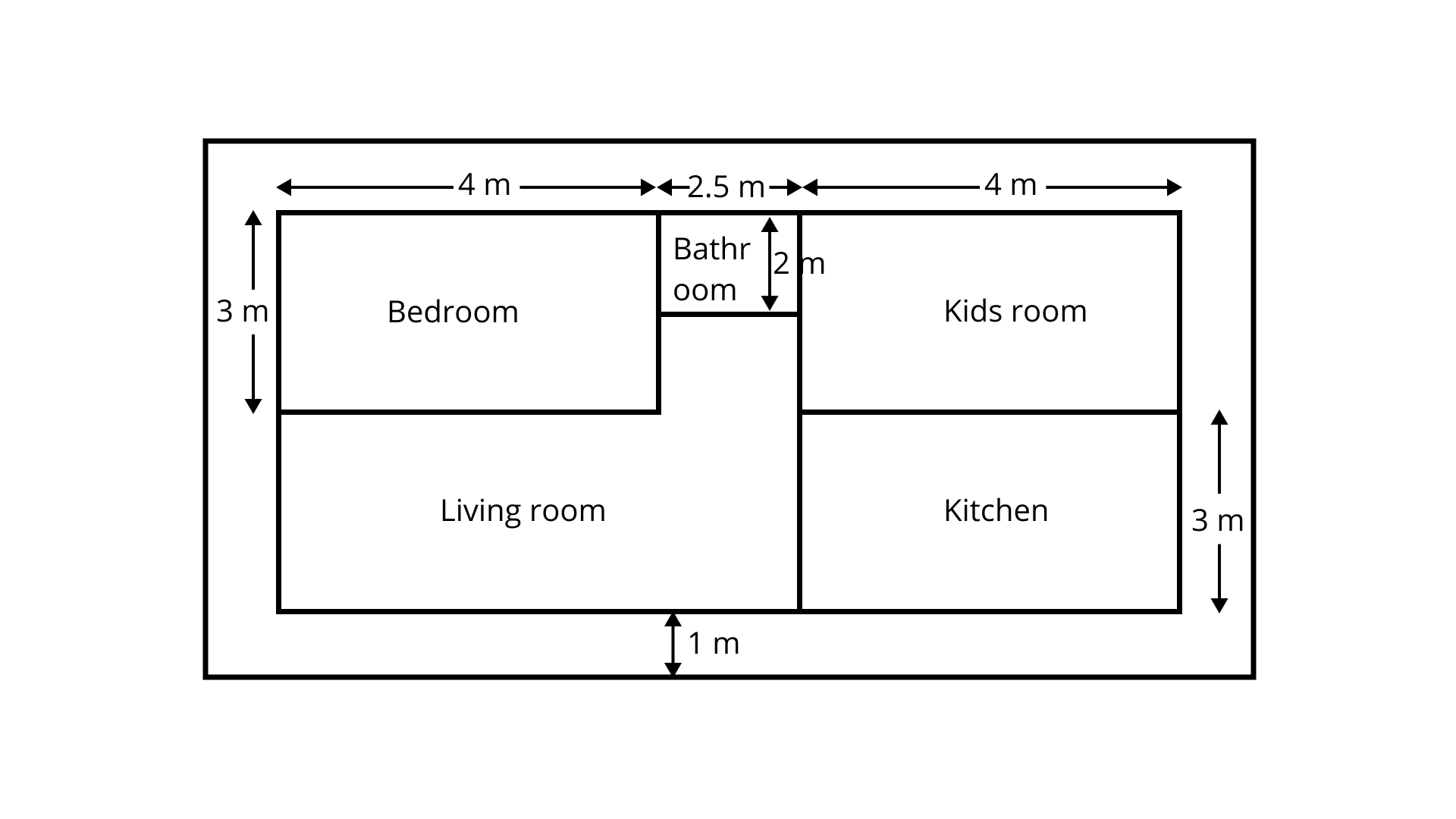
Find the following:

(i) Cost of paving the path with bricks at rate of ₹ \[{\mathbf{120}}\] per ${{\text{m}}^2}$.

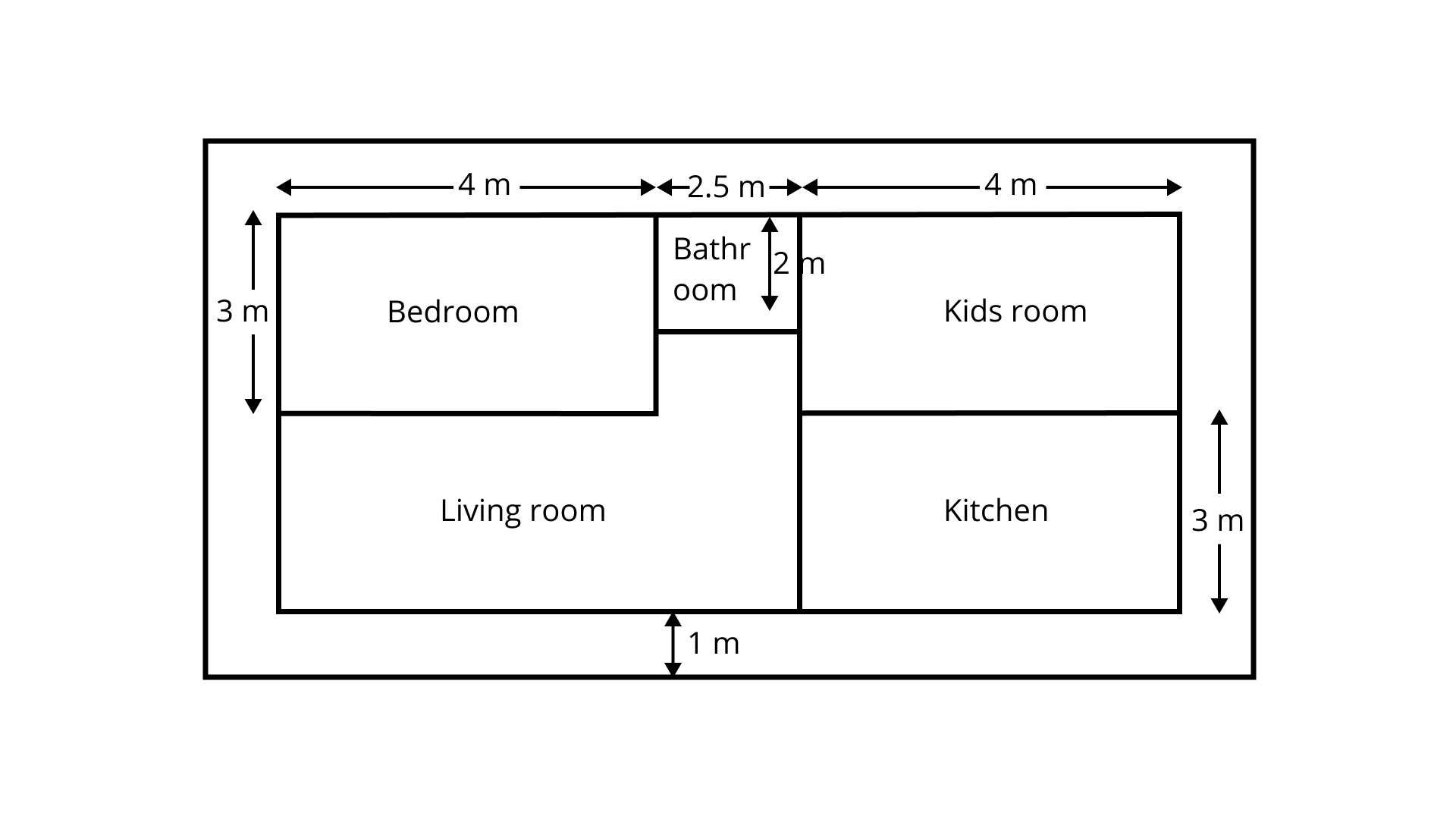
Ans: Area of path = Area of rectangle PQRS - area of rectangle ADFH

$ = {\text{PQ}} \times {\text{QR}} - {\text{AD}} \times {\text{DF}}$

Given,

${\text{PQ}} = (4 + 2.5 + 4 + 1 + 1) = 12.5$

${\text{QR}} = (3 + 3 + 1 + 1) = 8$

${\text{AD}} = (4 + 2.5 + 4) = 10.5$

${\text{DF}} = (3 + 3) = 6$

By putting these values in equation (i);

$ = 12.5 \times 8 - 10.5 \times 6 = 37\;{{\text{m}}^2}$

Now,

Cost of paving the path with bricks$ = $cost per unit ${{\text{m}}^2} \times $ total area of path

$ = 120 \times 37 = {\text{ Rs}}{\text{. }}4440$

(ii) Cost of wooden flooring inside the house except the bathroom at the cost of ₹ \[{\mathbf{1200}}\]per ${{\text{m}}^2}$.

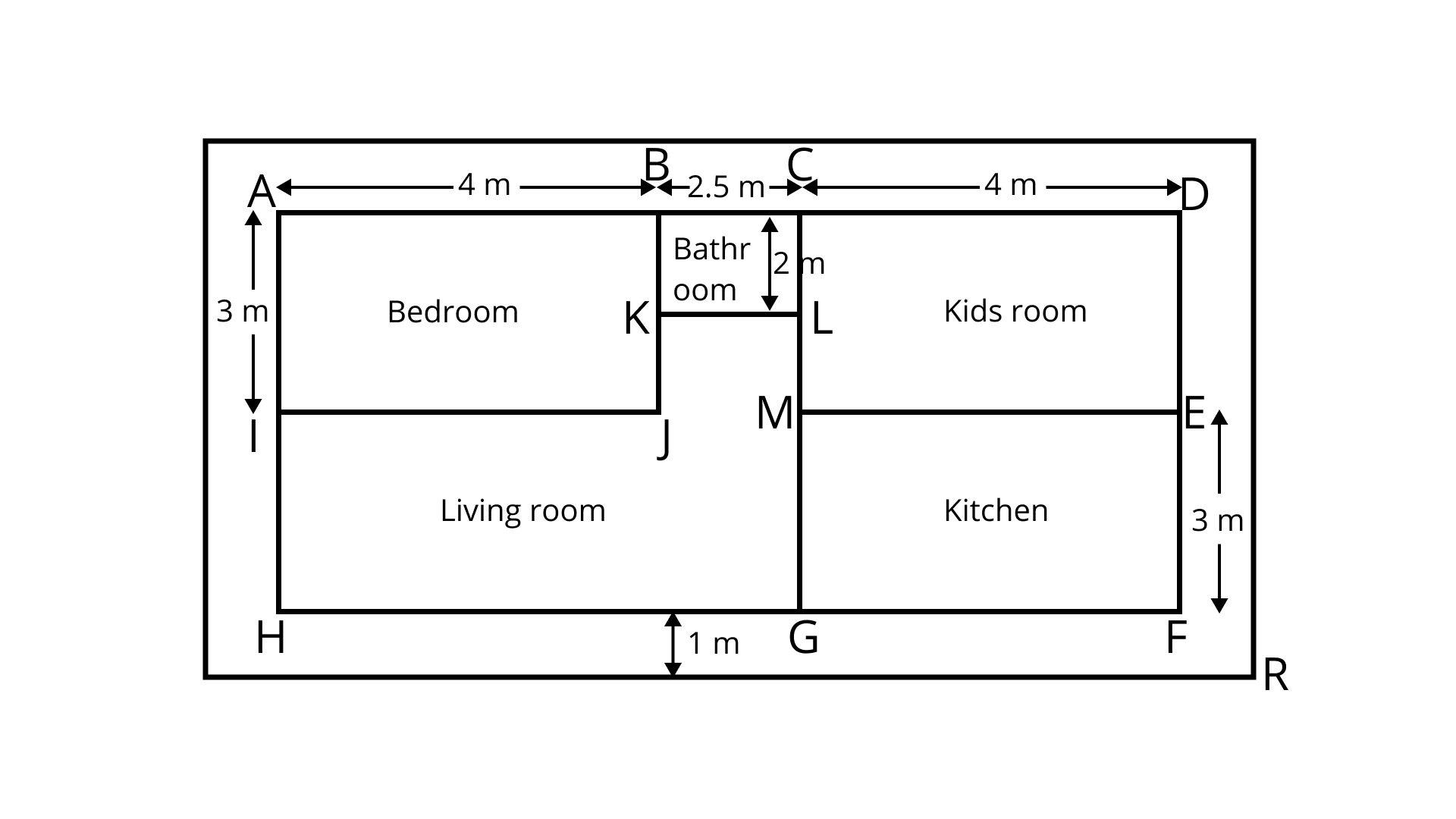
Ans: Area of house except bathroom = area of house\[\; - \]Area of bathroom

= Area of rectangle ${\text{ADFH}}$ - area of rectangle BCLK  ..(ii)

Given, Area of rectangle ${\text{ADFH}} = 63\;{\text{m}}$ and Area of rectangle BCLK $ = 5\;{\text{m}}$

By putting these values in equation (ii);

$ = 63 - 5 = 58\;{{\text{m}}^2}$

Now,

The cost of flooring = cost per unit ${{\text{m}}^2} \times $ Total area

$ = 1200 \times 58 = {\text{ Rs}}{\text{. }}69600.$

(iii) Area of Living Room.

Ans: Area of living room

= Area of rectangle ${\text{ACGH}}$ - Area of rectangle ${\text{ABJI}}$ - Area of rectangle BCLK ... (iii)

Given, Area of rectangle ${\text{ACGH}} = 39$,

Area of rectangle ${\text{ABJI}} = 12$ and 

Area of rectangle ${\text{BCLK}} = 5$

By putting these values in equation (iii), we get 

$ = 39 - 12 - 5 = 22\;{{\text{m}}^2}$

126. Architects design many types of buildings. They draw plans for houses, such as the plan shown in Fig. 9.68:

An architect wants to install decorative moulding around the ceilings in all the rooms. The decorative moulding costs Rs ${\mathbf{500/}}$ metre.

(a) Find how much moulding will be needed for each room.

(i) family room

(ii) living room

(iii) dining room

(iv) bedroom 1

(v) bedroom 2

Ans: 

(i) Perimeter of family room $ = 2$ (length + breadth) 

Given, length $ = 5.48\;{\text{m}}$ 

breadth $ = 4.57\;{\text{m}}$ 

By putting these values in above formula, we get 

$ = 2 \times (5.48 + 4.57) = 2 \times 10.05 = 20.10\;{\text{m}}$

ii. Perimeter of living room $ = 2$ (length +$breadth)$

$\operatorname{Given} ,length = 3.81\;{\text{m}}$

 breadth $ = 7.53\;{\text{m}}$ 

By putting these values in above formula, we get 

$ = 2 \times (3.81 + 7.53) = 2 \times 11.34 = 22.68\;{\text{m}}$

iii. Perimeter of dining room $ = 2$ (length +$breadth)$

$\operatorname{Given} ,length = 5.41\;{\text{m}}$and breadth $ = 5.48\;{\text{m}}$

By putting these values in above formula, we get

$ = 2 \times (5.41 + 5.48) = 2 \times 10.89 = 21.78\;{\text{m}}$

iv. Perimeter of bedroom $1 = 2$ (length +$breadth)$

$\operatorname{Given} ,length = 3.04\;{\text{m}}$and breadth $ = 3.04\;{\text{m}}$

By putting these values in above formula, we get

$ = 2 \times (3.04 + 3.04) = 2 \times 6.08 = 12.16\;{\text{m}}$

v. Perimeter of bedroom $2 = 2$(length $ + $ breadth)

Given, length $ = 3.04\;{\text{m}}$and breadth $ = 2.43\;{\text{m}}$

By putting these values in above formula, we get 

$ = 2 \times (3.04 + 2.43) = 2 \times 5.47 = 10.94\;{\text{m}}$

(b) The carpet costs Rs ${\mathbf{200/}}{{\mathbf{m}}^{\mathbf{2}}}$. Find the cost of carpeting each room.

Ans: 

For bedroom 1,

Given, length of bedroom $1 = 3.04\;{\text{m}}$ and breadth of bedroom $1 = 3.04\;{\text{m}}$

Area of bedroom $1 = $ Length ${\text{x}}$ Breadth

Area of bedroom $1 = 3.04 \times 3.04 = 9.2416{\text{sqm}}$

Cost of carpeting $1{\text{sqm}} = $ Rs. 200

Cost of carpeting $9.2416\;{{\text{m}}^2} = 9.2416 \times 200 = Rs{\text{ }}1848$ 

For bedroom 2 ,

Given, length of bedroom $2 = 3.04\;{\text{m}}$

and breadth of bedroom $2 = 2.43\;{\text{m}}$

Area of bedroom $2 = $ Length $ \times $ Breadth

$ = 304 \times 2.43 = 7.3872\;{{\text{m}}^2}$

Cost of carpeting $1\;{{\text{m}}^2} = $ Rs. 200

Cost of carpeting $7.3872\;{{\text{m}}^2} = 7.3872 \times 200 = Rs1477$

For living room,

Given, length of living room $ = 3.81\;{\text{m}}$ and

breadth of living room $ = 7.53\;{\text{m}}$

Area of living room $ = 3.81 \times 7.53 = 28.6893\;{{\text{m}}^2}$

Cost of carpeting of living room $1\;{{\text{m}}^2} = {\text{Rs}}200$.

Cost of carpeting $28.6893\;{{\text{m}}^2} = {\text{Rs}}.200 \times 286893$

$ = {\text{Rs}}.5737.86$

For dining room,

Given, length of dining room $ = 5.41\;{\text{m}}$ and breadth of dining room $ = 5.48\;{\text{m}}$

Area of dining room $ = 5.41 \times 5.48 = 29.6468\;{{\text{m}}^2}$

Cost of carpeting $1\;{{\text{m}}^2} = $ Rs. 200

Cost of carpeting $29.6468\;{{\text{m}}^2} = 29.6468 \times 200 = Rs5929.36$ 

For the family room,

Given, length of family room $ = 4.57\;{\text{m}}$ Breadth of family room $ = 5.48\;{\text{m}}$

Area of family room $ = 5.48 \times 4.57 = 5.0436\;{{\text{m}}^2}$ 

Therefore, cost of carpeting family room $ = 25.0436 \times 200 = Rs.{\text{ }}5008.7$ 

(c) What is the total cost of moulding for all the five rooms.

Ans: Total perimeter of all the five rooms, 

$ = 20.10\;{\text{m}} + 22.68\;{\text{m}} + 21.78\;{\text{m}} + 12.16\;{\text{m}} + 10.94\;{\text{m}}$ 

$ = 87.66\;{\text{m}}$

Given, cost of moulding each room = Rs. 500 per m 

Now, the total cost of moulding all 5 rooms 

$ = 87.66 \times 500 = Rs.{\text{ }}43830$ 

127. ${\mathbf{ABCD}}$ is a given rectangle with length as ${\mathbf{80\;cm}}$ and breadth as ${\mathbf{60\;cm}}{\mathbf{.P,Q,R,S}}$ are the mid points of sides ${\mathbf{AB,BC,CD,DA}}$ respectively. A circular rangoli of radius ${\mathbf{10\;cm}}$ is drawn at the centre as shown in Fig. 9.69. Find the area of the shaded portion.

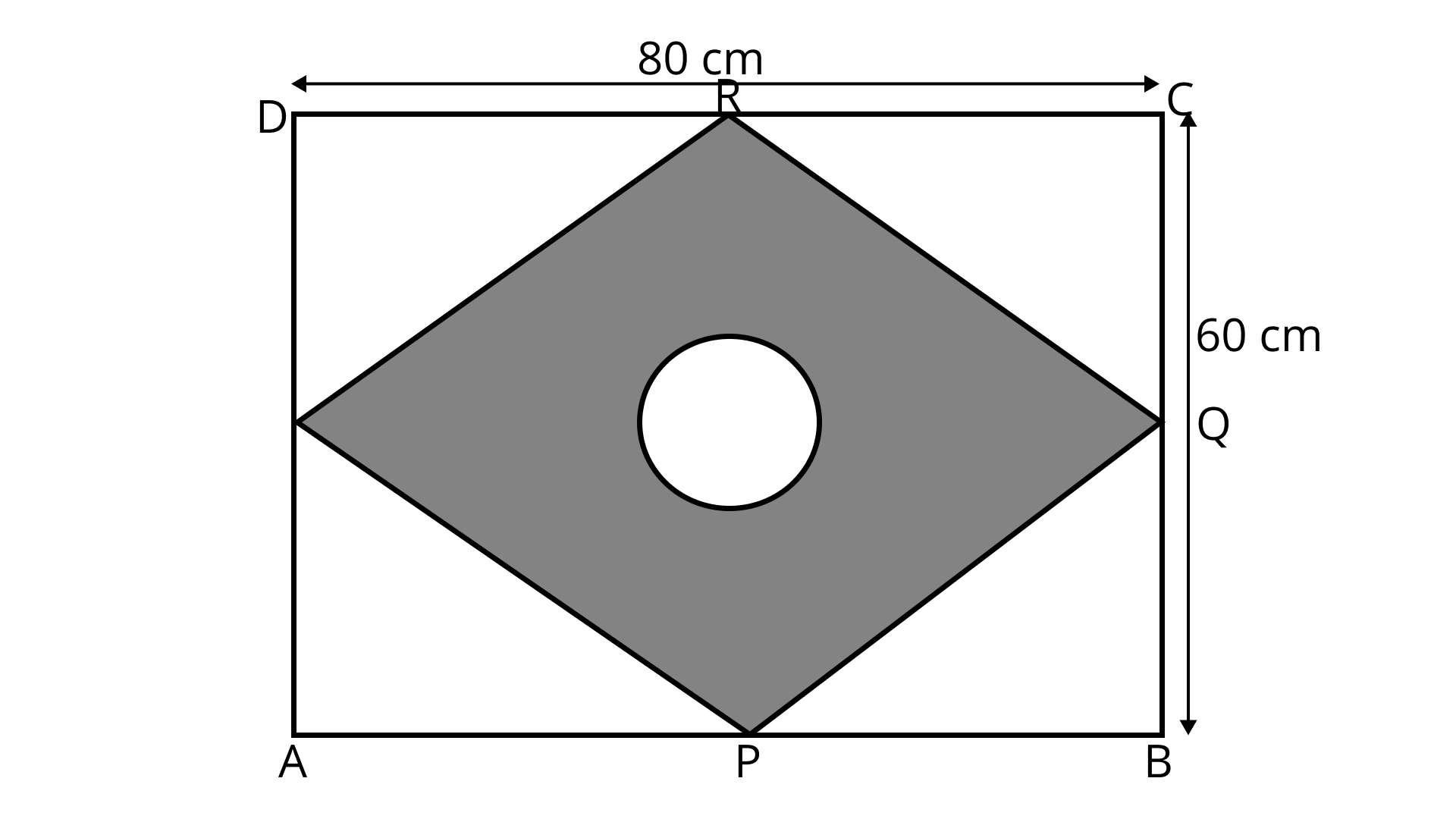
Ans: Here,

$AP = \dfrac{1}{2}AB$

$ = \dfrac{1}{2} \times 80$

$ = \dfrac{1}{2} \times 80 = 40{\text{cm }}$

Now,

$AS = \dfrac{1}{2}AD$

$ = \dfrac{1}{2} \times 60 = 30\;{\text{cm}}$

Area of triangle APS

$ = \dfrac{1}{2} \times AP \times AS$

$ = \dfrac{1}{2} \times 40 \times 30 = 600{\text{c}}{{\text{m}}^2}$

Area of portion PQRS = Area of rectangle ABCD -4 times of triangle APS

$ = 80 \times 60 - 4 \times 600$

$ = 48000 - 2400$

$ = 2400\;{\text{c}}{{\text{m}}^2}$

Area of circular rangoli, $ = \pi  \times {(10)^2}$

$ = \dfrac{{22}}{7} \times 100$ $ = 314\;{\text{c}}{{\text{m}}^2}$

Area of shaded portion, 

$ = 2400 - 314 = 2086\;{\text{c}}{{\text{m}}^2}$

128. 4 squares each of side ${\mathbf{10\;cm}}$ have been cut from each corner of a rectangular sheet of paper of size ${\mathbf{100\;cm \times 80\;cm}}$. From the remaining piece of paper, an isosceles right triangle is removed whose equal sides are each of ${\mathbf{10\;cm}}$ length. Find the area of the remaining part of the paper.

Ans: Area of each square $ = 100\;{\text{c}}{{\text{m}}^2}$

Area of rectangular sheet $ = 100 \times 80\;{\text{c}}{{\text{m}}^2} = 8000\;{\text{c}}{{\text{m}}^2}$

Area of an isosceles right triangle $ = \dfrac{1}{2} \times 10 \times 10 = 50\;{\text{c}}{{\text{m}}^2}$

Area of remaining part of paper $ = 8000 - 4 \times 100 - 50$ 

$ = 7550\;{\text{c}}{{\text{m}}^2}$

129. A dinner plate is in the form of a circle. A circular region encloses a beautiful design as shown in Fig. 9.70. The inner circumference is ${\mathbf{352\;mm}}$ and the outer is ${\mathbf{396\;mm}}$. Find the width of the circular design.

Ans: Let $R$ be radius of outer circle and $r$ be radius of inner circle,

It has been given that $352\;{\text{mm}}$ is the circumference of inner circle,

$2\pi r = 352{\text{mm }}$

$r = \dfrac{{352 \times 7}}{{2 \times 22}}$

$ = \dfrac{{2464}}{{44}} = 56{\text{mm}}$

In addition, $396\;{\text{mm}}$ is the circumference of outer circle, 

$2\pi R = 396\;{\text{mm}}$

$r = \dfrac{{396 \times 7}}{{2 \times 22}} = 63\;{\text{mm}}$

Therefore, width of circular design $ = {\text{R}} - {\text{r}} = 63 - 56 = 7\;{\text{mm}}$

130. The moon is about ${\mathbf{384000\;km}}$ from earth and its path around the earth is nearly circular. Find the length of path described by the moon in one complete revolution. (Take ${\mathbf{\pi  = 3}}{\mathbf{.14}}$ )

Ans: Length of path described by moon in one complete revolution $ = 2\pi r$ 

$ = 2 \times 3.14 \times 384000$ 

$ = 2411520\;{\text{km}}$

131. A photograph of Billiard/Snooker table has dimensions as $\dfrac{{\mathbf{1}}}{{{\mathbf{10}}}}$ th of its actual size as shown in Fig. 9.71:

The portion excluding six holes each of diameter ${\mathbf{0}}{\mathbf{.5\;cm}}$ needs to be polished at rate of ₹ \[{\mathbf{200}}\] per ${{\text{m}}^2}$. Find the cost of polishing.

Ans: Actual breadth $ = 10 \times 10 = 100\;{\text{cm}}$ 

Actual length $ = 25 \times 10 = 250\;{\text{cm}}$ 

Area of table $ = 250 \times 100 = 25000\;{\text{c}}{{\text{m}}^2}$

Radius on one hole $ = \dfrac{{0.5}}{2} = 0.25\times 10 =2.5$ 

Area of 6 holes, $ = 6 \times \pi {r^2} = 6 \times \dfrac{{22}}{7} \times 2.5 \times 2.5$

$ = 117.85\;{\text{c}}{{\text{m}}^2}$

Area of excluding holes, $ = 25000 - 118 = 24882.15\;{\text{c}}{{\text{m}}^2}$ 

Therefore, cost of polishing $ = \dfrac{{24882.15}}{{10000}} \times 200 = Rs.500$

Easy Solutions for NCERT Exemplar Class 7 Chapter 9

Vedantu offers the NCERT Exemplar for Class 7 Maths Solutions Chapter - 9 Perimeter & Area to the students which are completely free of cost. This NCERT Exemplar for Class 7 Maths Solutions Chapter - 9 Perimeter & Area is provided in PDF format, which can be downloaded by the students to study offline. 

The subject experts at Vedantu had prepared these solutions: The NCERT Exemplar for Class 7 Maths Solutions Chapter - 9 Perimeter & Area appropriately. All these solutions are made following the latest NCERT syllabus and guidelines. These solutions are made to help and guide students and get them prepared for examinations. These solutions assist students in their homework and assignments too. Students can certainly do well in the final exams and ace the subject by practising these solutions. 

All the sections of this chapter and exercises have been properly covered in this solution file. The prime aim of the experts of Vedantu is to provide the ideal solutions that students can easily grab and work on. They can refer to these solutions to understand how to approach such problems and solve them within a shorter period. To become efficient in solving problems related to perimeter and area, download this file today and add it to your study material.