CBSE Class 7 Maths The Triangle and Its Properties Notes - Chapter 6 Free PDF

Triangles:

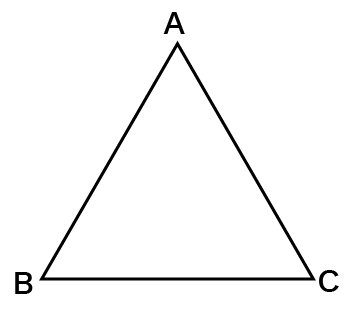
• Triangles are three line segments that form a closed plane figure.

• In above figure, $\vartriangle \text{ABC}$ is a triangle.

• The three angles and three sides of a triangle make up the triangle's six constituents.

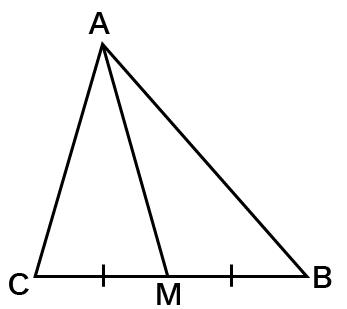
• The line segment connecting a triangle's vertex to the opposite side's midpoint is known as the triangle's median. 

• In above figure, $\text{AM}$ is the median of triangle $\text{ABC}$.

• There are three medians in a triangle.

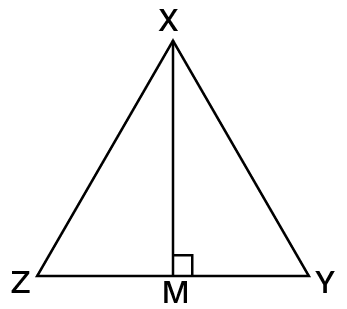
• The perpendicular line segment connecting a triangle's vertex to its opposite side is known as the triangle's height or altitude of a triangle. 

• In above figure, $\text{XM}$ is the altitude (height) of triangle $\text{XYZ}$.

• There are three elevations in a triangle.

Type of Triangle Based on Sides:

• Equilateral Triangle:

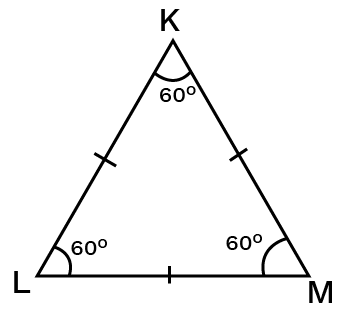
If each of a triangle's sides is the same length, then the triangle is said to be equilateral. 

Each angle in an equilateral triangle is $60$ degrees.

• Isosceles Triangle:

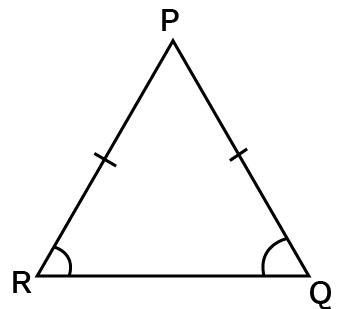
If at least two of the triangle's sides are the same length, then it is said to be isosceles. 

• An isosceles triangle's base is its non-equal side.

• The base angles of an isosceles triangle have equal measures.

• Scalene Triangle:

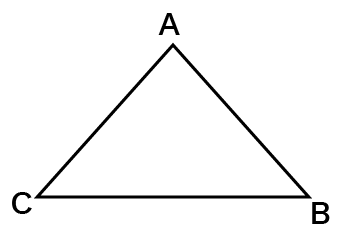
• All of the sides of a triangle are different lengths. 

• There are no two angles that are the same.

Property of the Lengths of Sides of a Triangle:

• Any two sides of a triangle have a length that is more than the length of the third side.

• The length difference between any two sides is smaller than the length difference between the third and fourth sides. 

• This feature is important for determining whether or not a triangle may be drawn when the lengths of the three sides are known.

Types of Triangle-based on Angles:

1. Right Angled Triangle: 

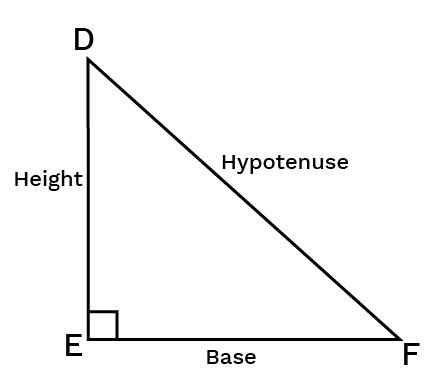
• A triangle in which one of the angles is measured in ${{90}^{0}}$.

• The hypotenuse is the side opposite the right angle of a right-angled triangle, whereas the legs are the other two sides.

2. Obtuse Angled Triangle:

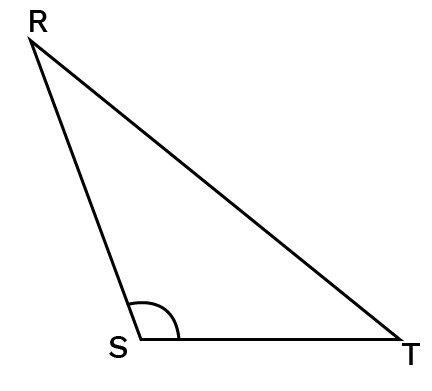
A triangle in which one of the angles is larger than ${{90}^{0}}$.

3. Acute Angled Triangle:

A triangle in which each of the angles is smaller than ${{90}^{0}}$.

Pythagoras Property:

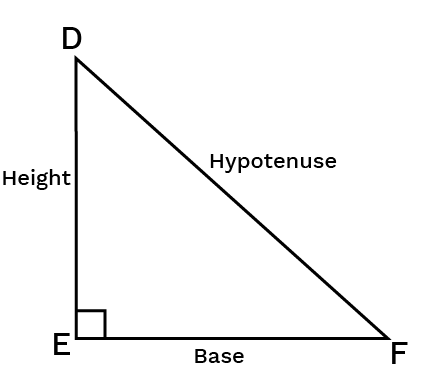
• In right-angled triangle, the square on the hypotenuse equals the sum of the squares on the legs of a right-angled triangle. 

• Triangle $\text{DEF}$ is a right angled triangle. According to Pythagoras Theorem,

\[{{\left( Hypotenuse \right)}^{2}}\text{ }=\text{ S}um\text{ }of\text{ }the\text{ }squares\text{ }on\text{ }the\text{ }legs.\]

Therefore,

${{\left( \text{DF} \right)}^{2}}={{\left( \text{DE} \right)}^{2}}+{{\left( \text{EF} \right)}^{2}}$

• This property does not hold true if a triangle is not right-angled. 

• This feature can be used to determine whether or not a triangle is right-angled.

Exterior Angle:

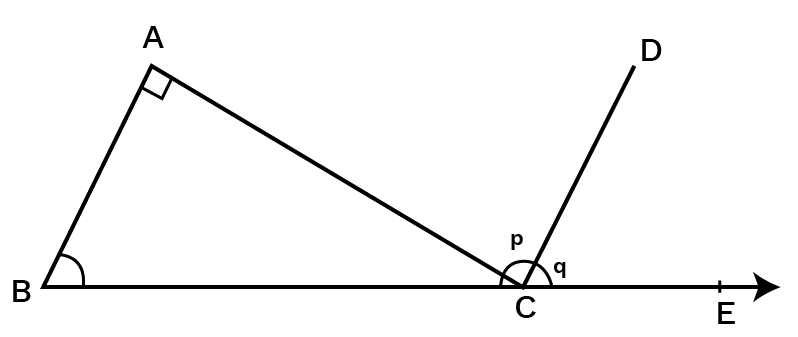
• The sum of a triangle's internal opposite angles equals its outer angle that is known as the Exterior angle of a triangle.

• In above figure, $\angle \text{ACE}$ is an Exterior angle.

\[\angle \text{ACE = }\angle \text{A}+\angle \text{B}\]

• When a side of a triangle is made, an external angle of a triangle is formed. 

• There are two ways to generate an external angle at each vertex.

A Property of Exterior Angles:

The sum of the measures of a triangle's internal opposite angles equals the measure of any of its outer angles.

The Angle Sum Property of a Triangle:

The total measure of a triangle's three angles is ${{180}^{0}}$.

Property of the Lengths of Sides of a Triangle:

• The lengths of any two sides of a triangle are always bigger than the third side's length. 

• The length difference between any two triangle sides is always less than the length of the third side.

Benefits of CBSE Class 7 Maths Chapter 6 Revision Notes

Here are a few points that tell us the benefits of CBSE Class 7 Maths Revision Notes:

• These notes are your one-stop solution for last-minute exam preparation.

• The topic-wise key points included in these revision notes will help you to revise all the chapters easily and also to brush up on the concepts.

• Class 7 Maths Chapter 6 Revision Notes are made by the subject experts at Vedantu, so you can rely on these answers completely.

• Referring to the CBSE Class 7 Maths Chapter 6 Revision Notes will help students improve their understanding of all the topics which are provided here in a detailed manner.

• These notes can be downloaded for free in PDF format and can be accessed from anywhere. 

Conclusion

Vedantu's free PDF notes on CBSE Class 7 Maths Chapter 6, "The Triangle and Its Properties," are a valuable educational resource. These notes serve as a comprehensive guide, covering essential topics related to triangles, including properties, theorems, and practical applications. They cater to the needs of CBSE Class 7 students, ensuring that they have access to high-quality study materials.

Vedantu's commitment to providing free, accessible educational content is commendable, as it empowers students to excel in their mathematical studies. These notes facilitate a deeper understanding of geometric concepts, helping students build a strong foundation in mathematics. By utilising these resources, students can enhance their problem-solving skills, geometry proficiency, and overall academic performance, making them an indispensable asset for students and educators alike.