Question

Use Huygene's principle to explain the formation of diffraction patterns due to a single slit illuminated by a monochromatic source of light.
When the width of the slit is made double the original width, how would this affect the size and intensity of the central diffraction band?

Answer 1

Hint: According to Huygens principle, the net effect at any point due to a number of wavelets is equal to the sum total of contribution of all wavelets with proper phase difference. The single slit mathematical derivations follow a similar method to that for double-slit diffraction.

Formula Used: The formulae used in the solution are given here.
Intensity $I = {I_0}\dfrac{{{{\sin }^2}\alpha }}{\alpha }$ where $\alpha = \dfrac{{\pi b\sin \theta }}{\lambda }$.
Width of central maxima is given by $\beta = \dfrac{{2D\lambda }}{b}$ where $D$ is the distance between the screen and slit, $\lambda $ is the wavelength of the light and $b$ is the size of the slit.

Complete step by step answer
Light passing through a single slit also diffracts. According to Huygens Principle, every point along a wavefront can be treated as the source of a spherical wavelet.
The Huygens–Fresnel principle, called after Dutch physicist Christiaan Huygens and French physicist Augustin-Jean Fresnel is a process of summary referred to difficulties of wave proliferation both in the far-field boundary and in near-field diffraction and also appearance. It states that all limits on a wavefront is itself the cause of astronomical wavelets, and the trivial wavelets radiating from various points together intervene. The amount of certain round wavelets makes the wavefront.

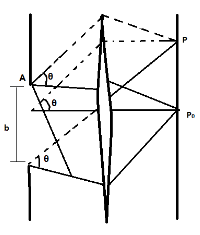
Consider a parallel beam of monochromatic light that is incident normally in a slit of width $b$as shown in the figure. Consider a particular point P on the screen receives waves from all the secondary sources. All these waves start from different places and give the resultant intensity at the point P. At ${P_0}$​ all waves are travelling on the same optical path. As the all waves are in phase thus the interference of maximum intensity is observed.
The intensity at the point P is given by $I = {I_0}\dfrac{{{{\sin }^2}\alpha }}{\alpha }$ where $\alpha = \dfrac{{\pi b\sin \theta }}{\lambda }$.
For central maxima, $\alpha = 0$, so $I = {I_0}$.
Width of central maxima is given by $\beta = \dfrac{{2D\lambda }}{b}$ where $D$ is the distance between the screen and slit, $\lambda $ is the wavelength of the light and $b$ is the size of the slit.
So with the increase in size of the slit the width of the central maxima decrease. Hence double the size of the slits would result in half the width of the central maxima.

Note
Single slit diffraction is very similar to double-slit diffraction. The similarities have been stated below.
-The double slit sees the outer boundaries of the slit as a single slit.
-The "single slit nature" of double slit diffraction is seen in the envelope of the double slit fringes.
-The minima of the envelope are the same as the minima for a single slit with the same slit width as the overall width of the double slit.