Question

Two sources ${S_1}$ and ${S_2}$ of same frequency $f$ emit sound. The sources are moving as shown in figure 1 with speed $u$each. A stationary observer hears that sound. The beat frequency is? ( $v = 0$ velocity of sound)

A. $\dfrac{{2{v^2}f}}{{{v^2} - {u^2}}}$
B. $\dfrac{{2u}}{v}f$
C. $\dfrac{{2{u^2}f}}{{{v^2} - {u^2}}}$
D. $\dfrac{{2uvf}}{{{v^2} - {u^2}}}$

Answer 1

Hint: In the case of a problem based on wave phenomena, we know that all the parameters such as i.e., frequency, amplitude, time period, etc., vary with each other in some way hence, analyze every option given in this question and use mathematical calculation by finding the apparent frequency of both the sources with the information given.

Formula used:
The expression of apparent frequency (${f_1}$) of source ${S_1}$ is,
${f_1} = f\left( {\dfrac{{v - 0}}{{v - u}}} \right) = \dfrac{v}{{v - u}}f$
Here, $v$ is the velocity of sound and $u$ is the velocity of source.

Complete step by step solution:
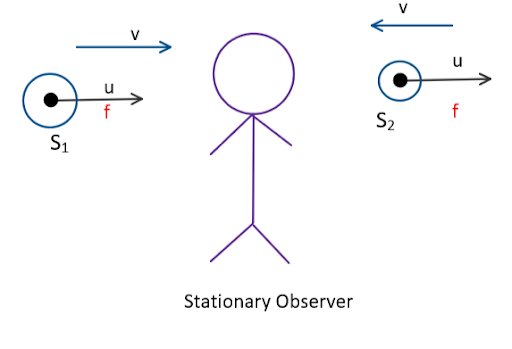
Two Sources ${S_1}$ and ${S_2}$ of the same frequency $f$ emit sound (given) and these sources are moving in the same direction as shown in figure 2. The velocity of the two sources is again same i.e., $u$(given). And, velocity of sound $v = 0$ (given). As the observer is stationary, therefore, the direction of sound waves must be opposite in direction as shown in figure 2.

Now, Apparent frequency of source ${S_1}$ will be:
${f_1} = f\left( {\dfrac{{v - 0}}{{v - u}}} \right) = \dfrac{v}{{v - u}}f$ … (1)
And, Apparent frequency of source ${S_2}$ will be:
${f_2} = f\left( {\dfrac{{v - 0}}{{v + u}}} \right) = \dfrac{v}{{v + u}}f$ … (2)
We know that Beat Frequency $f'$ can be calculated as:
$f' = {f_1} - {f_2}$

Substitute the values of ${f_1}$ and ${f_2}$ in the above expression, we get
$f' = \dfrac{v}{{v - u}}f - \dfrac{v}{{v + u}}f$
Taking $vf$common, we get
$f' = vf\left( {\dfrac{{v + u - (v - u)}}{{(v - u)(v + u)}}} \right)$
$\Rightarrow f' = vf\left( {\dfrac{{2u}}{{{v^2} - {u^2}}}} \right)$........(Because, ${a^2} - {b^2} = (a - b)(a + b)$)
Thus, according to the given question, the beat frequency for the two sources is $\dfrac{{2uvf}}{{{v^2} - {u^2}}}$.

Hence, the correct option is D.

Note: Since this is a conceptual-based problem on wave and acoustics hence, it is essential that given sources and their conditions must be analyzed very carefully to give a precise explanation of the solution. While writing an answer always remember to use the mathematical proven relations to provide an accurate solution.