Question

The variation of the acceleration a of the particle executing S.H.M.with displacement x is as shown in the figure
A.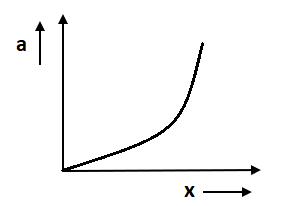
B.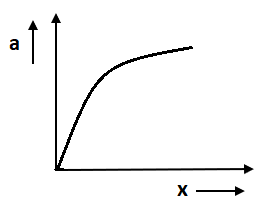
C.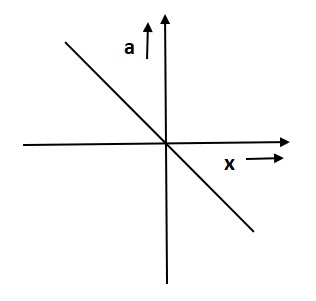
D.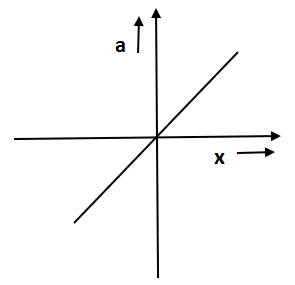

Answer 1

Hint: Here the graph is given between acceleration(a) and displacement(x). So, to find the correct graph we need to use the relation between acceleration and displacement in simple harmonic motion. By using the relation between the acceleration and the displacement of the SHM we can easily draw the graph between them.

Formula used:
The acceleration (a) of the particle executing simple harmonic motion (SHM) is given as,
\[a = - {\omega ^2}A\sin (\omega t + \phi )\]
\[\Rightarrow a = - {\omega ^2}x\]
Where \[\omega \] is angular frequency, A is the amplitude, t is the time taken, \[\phi \] is the phase constant and x is the displacement.

Complete step by step solution:
As we know that the displacement x in simple harmonic motion (SHM) is given as,
\[x = A\sin (\omega t + \phi ) \\ \]
Also, the acceleration a of the particle executing simple harmonic motion (SHM) is given as,
\[a = - {\omega ^2}A\sin (\omega t + \phi ) \\ \]
Now the acceleration(a) of the particle which is related to the displacement (x) executing a simple harmonic motion (SHM) is
\[a = - {\omega ^2}x \\ \]
Here acceleration a and displacement x are linearly dependent on each other.
This equation shows the straight-line equation passing through origin as,
\[y = mx + c \\ \]
So, after comparing both we get a negative slope. In option C and D a straight line is given. In option D slope is positive as the angle is positive whereas in option C slope is negative.

Hence option C is the correct answer.

Note: Simple Harmonic Motion (SHM) is defined as a motion in which the restoring force(F) is directly proportional to the displacement(x) of the body from its mean position or equilibrium position. It can also be known as an oscillatory motion in which the acceleration of the body at any position is directly proportional to the displacement which is from the mean position.