Question

The value of ‘g’ on the surface of the earth is
A. Maximum at poles
B. Maximum at equator
C. Same everywhere
D. Minimum at poles

Answer 1

Hint: Solution can be found by observing the gravitational attraction formula, where gravitational force is inversely proportional to the distance from the center of the earth. Thus, extending it to the concept that Earth is not a perfect sphere and the distance of poles and the equator is different from the center of earth.

Complete step-by-step answer:
Gravitational attractive force felt by a body on the earth’s surface is given as;
$\overset{\to }{\mathop{F}}\,=\dfrac{GMm}{{{r}^{2}}}$
G is the gravitational constant
r is the distance from the earth’s center
M is the mass of the earth
M is the mass of the body.

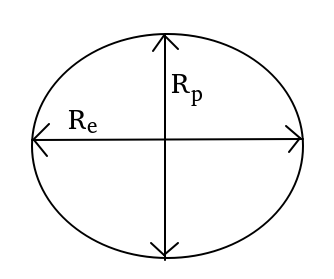
We can observe from the above image that earth is not a perfect sphere. It is slightly bulged at the equator, and flattened at the poles. Thus, from the above diagram we can observe that;
$R_e > R_p$
where, $R_e$ is the diameter at the equator, $R_p$ is the diameter at the poles
We know from the gravitational attraction and thus the acceleration due to gravity ‘g’ becomes:
$\begin{align}
  & g=\dfrac{GM}{{{r}^{2}}} \\
 & \Rightarrow g\propto \dfrac{1}{{{r}^{2}}} \\
\end{align}$

Thus, for poles:
${{g}_{p}}\propto \dfrac{1}{R_{p}^{2}}$
Thus, for equator:
${{g}_{p}}\propto \dfrac{1}{R_{e}^{2}}$
So, since ${{R}_{e}}>{{R}_{p}},{{g}_{e}}$ will be less than ${{g}_{p}}$. That is, gravitational force and the ‘g’ will be maximum at the poles.
Therefore, the correct answer to this question is option A. That is ‘g’ is maximum at poles.
Note: The gravitational force is an attractive force that is, it always attracts and never repels. It never pushes two masses further, only a pulling force is generated. The ‘g’ is the acceleration of gravity and is equal to $9.8m/{{s}^{2}}$ at Earth surface, i.e., at sea level.