Question

The sides of a triangular plate are $8cm$,$15cm$and$17cm$.If its weight is $96gm$,find the weight
of the plate per square $cm$.
$\left( A \right)$.$1.6gm$
$\left( B \right)$.$0.8gm$
$\left( C \right)$.$1.4gm$
$\left( D \right)$.$2gm$

Answer 1

Hint: Use Heron’s formula to compute the area of the triangular plate and find weight per square cm by dividing the weight by area of the triangle.

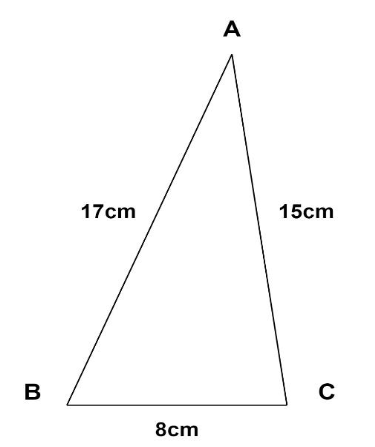
Let $ABC$be the triangular plate with sides
$
AB = 17cm \\
AC = 15cm \\
BC = 8cm \\

$
Given the problem, the weight of this triangular plate is $w = 96gm$.
In order to find the weight of the plate per square $cm$, we first need to compute the area of the
same.
Since sides of the triangular plate are given, we can use Heron’s formula to calculate the area of the
plate.
Heron’s formula states that area of the triangle is given by,
\[\Delta = \sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)} {\text{ (1)}}\]
In the above equation, $s$ is the semi-perimeter of the triangle and $a,b,c$ are the sides of the
triangle.
Sides of the triangular plate $ABC$are given by
$\left(
a = AB = 17cm \\
b = BC = 8cm \\
c = AC = 15cm \\
\right){\text{ (2)}}$
Semi-perimeter of triangle $ABC$ is given by,
$
s = \dfrac{{a + b + c}}{2} \\
\Rightarrow s = \dfrac{{17 + 8 + 15}}{2} = 20cm{\text{ (3)}} \\
$
Using equation $(2)$and $(3)$ in $(1)$,we get
\[
\Delta = \sqrt {20\left( {20 - 17} \right)\left( {20 - 8} \right)\left( {20 - 15} \right)} \\
\Rightarrow \Delta = \sqrt {20\left( 3 \right)\left( {12} \right)\left( 5 \right)} = 60c{m^2} \\
\]
Therefore, weight of the triangular plate per square $cm = \dfrac{w}{\Delta } =
\dfrac{{96gm}}{{60c{m^2}}} = 1.6gm$per $c{m^2}$.
Hence the correct option is $\left( A \right)$.$1.6gm$ .

Note: Heron’s formula should be used to compute the area where sides of the triangle are given. In
the problems like above, units need to be mentioned in the final answer.