
The graph $F - x$ is given, find the compression produced in the spring when a body of mass $5kg$ moving with velocity $8m/s$ hits the spring. Also calculate the force constant of the spring.
Answer
216k+ views
Hint: To find the force constant of the spring see the graph and find the slope. Then, calculate it by putting values. Now, to calculate the compression we have to use the conservation of energy in which total energy in an isolated system remains constant. So, kinetic and potential energy become equal to each other.
Complete step by step answer:
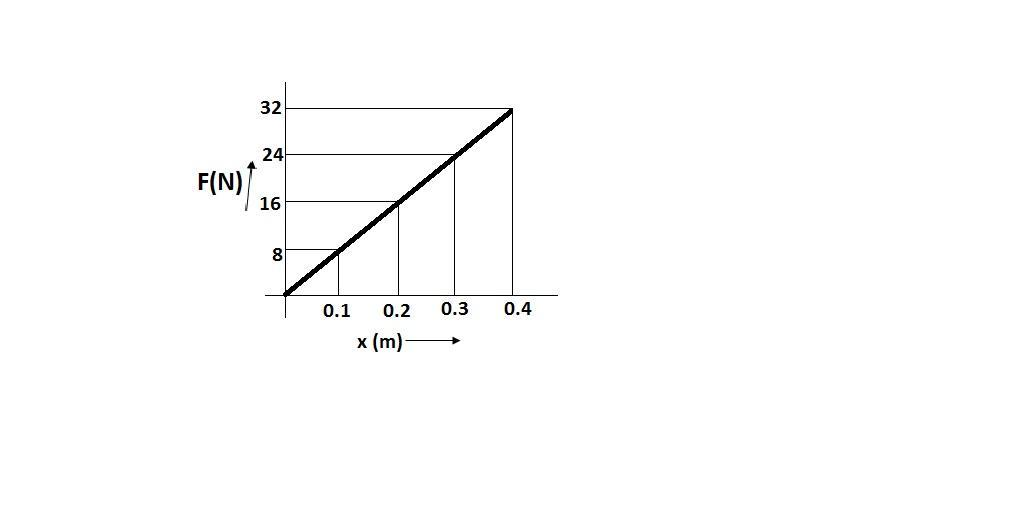
From the graph in the question, we can conclude that the slope of the graph is the force constant of the spring.
$
\because F = kx \\
\therefore k = \dfrac{x}{F} \\
$
where, $F$ is the force
$k$ is the force constant
$x$ is the compression of the spring
The slope of a graph can be calculated when we determine the difference between coordinates of the y – axis and x – axis respectively. After this, the differences of y – coordinates and x – coordinates are divided.
If we take $\left( {0.3m,24N} \right)$ and $\left( {0.2m,16N} \right)$ coordinates from x – axis and y – axis respectively, we get –
$
\implies Slope = \dfrac{{24 - 16}}{{0.3 - 0.2}} \\
\Rightarrow Slope = \dfrac{8}{{0.1}} \\
Slope = 80N/m \\
$
We know that, $slope = k$
Therefore, the force constant of the spring is $80N/m$.
From the question, we can conclude that the block will continue to compress till the block comes to the rest.
Now, using the conservation of energy the potential energy of the spring and kinetic energy of the spring becomes equal to each other because according to conservation of energy in an isolated system, the total energy remains constant and is said to be conserved over time.
$\therefore U = K \cdots \left( 1 \right)$
where, $U$ is the potential energy and $K$ is the kinetic energy
We know that, for a spring
$
\implies U = \dfrac{1}{2}k{x^2} \\
\implies K = \dfrac{1}{2}m{v^2} \\
$
From equation $\left( 1 \right)$, we get –
$\dfrac{1}{2}k{x^2} = \dfrac{1}{2}m{v^2}$
Cancelling $\dfrac{1}{2}$ on both sides, we get –
$
k{x^2} = m{v^2} \\
\implies x = v\sqrt {\dfrac{m}{k}} \cdots \left( 2 \right) \\
$
According to the question, it is given that –
Velocity, $v = 8m/s$
Mass, $m = 5kg$
Putting these values in equation $\left( 2 \right)$, we get –
$
\implies x = 8\sqrt {\dfrac{5}{{80}}} \\
\implies x = 8\sqrt {\dfrac{1}{{16}}} \\
\implies x = \dfrac{8}{4} = 2m \\
$
Hence, compression produced by the spring after the hitting of the body is $2m$.
Note: A spring stores potential energy due to extension. Since an unextended spring does not store potential energy, it is used as the point of zero energy. For a spring, potential energy is defined as, $U = \dfrac{1}{2}k{x^2}$ where, $x$ is the compression of the spring.
Complete step by step answer:
From the graph in the question, we can conclude that the slope of the graph is the force constant of the spring.
$
\because F = kx \\
\therefore k = \dfrac{x}{F} \\
$
where, $F$ is the force
$k$ is the force constant
$x$ is the compression of the spring
The slope of a graph can be calculated when we determine the difference between coordinates of the y – axis and x – axis respectively. After this, the differences of y – coordinates and x – coordinates are divided.
If we take $\left( {0.3m,24N} \right)$ and $\left( {0.2m,16N} \right)$ coordinates from x – axis and y – axis respectively, we get –
$
\implies Slope = \dfrac{{24 - 16}}{{0.3 - 0.2}} \\
\Rightarrow Slope = \dfrac{8}{{0.1}} \\
Slope = 80N/m \\
$
We know that, $slope = k$
Therefore, the force constant of the spring is $80N/m$.
From the question, we can conclude that the block will continue to compress till the block comes to the rest.
Now, using the conservation of energy the potential energy of the spring and kinetic energy of the spring becomes equal to each other because according to conservation of energy in an isolated system, the total energy remains constant and is said to be conserved over time.
$\therefore U = K \cdots \left( 1 \right)$
where, $U$ is the potential energy and $K$ is the kinetic energy
We know that, for a spring
$
\implies U = \dfrac{1}{2}k{x^2} \\
\implies K = \dfrac{1}{2}m{v^2} \\
$
From equation $\left( 1 \right)$, we get –
$\dfrac{1}{2}k{x^2} = \dfrac{1}{2}m{v^2}$
Cancelling $\dfrac{1}{2}$ on both sides, we get –
$
k{x^2} = m{v^2} \\
\implies x = v\sqrt {\dfrac{m}{k}} \cdots \left( 2 \right) \\
$
According to the question, it is given that –
Velocity, $v = 8m/s$
Mass, $m = 5kg$
Putting these values in equation $\left( 2 \right)$, we get –
$
\implies x = 8\sqrt {\dfrac{5}{{80}}} \\
\implies x = 8\sqrt {\dfrac{1}{{16}}} \\
\implies x = \dfrac{8}{4} = 2m \\
$
Hence, compression produced by the spring after the hitting of the body is $2m$.
Note: A spring stores potential energy due to extension. Since an unextended spring does not store potential energy, it is used as the point of zero energy. For a spring, potential energy is defined as, $U = \dfrac{1}{2}k{x^2}$ where, $x$ is the compression of the spring.
Recently Updated Pages
JEE Atomic Structure and Chemical Bonding important Concepts and Tips

JEE Amino Acids and Peptides Important Concepts and Tips for Exam Preparation

Electricity and Magnetism Explained: Key Concepts & Applications

Chemical Properties of Hydrogen - Important Concepts for JEE Exam Preparation

JEE Energetics Important Concepts and Tips for Exam Preparation

JEE Isolation, Preparation and Properties of Non-metals Important Concepts and Tips for Exam Preparation

Trending doubts
JEE Main 2026: Application Form Open, Exam Dates, Syllabus, Eligibility & Question Papers

Derivation of Equation of Trajectory Explained for Students

Hybridisation in Chemistry – Concept, Types & Applications

Understanding the Angle of Deviation in a Prism

Understanding Collisions: Types and Examples for Students

How to Convert a Galvanometer into an Ammeter or Voltmeter

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Units And Measurements Class 11 Physics Chapter 1 CBSE Notes - 2025-26

NCERT Solutions For Class 11 Physics Chapter 8 Mechanical Properties Of Solids

Motion in a Straight Line Class 11 Physics Chapter 2 CBSE Notes - 2025-26

NCERT Solutions for Class 11 Physics Chapter 7 Gravitation 2025-26

Ideal and Non-Ideal Solutions Explained for Class 12 Chemistry




