Question

The dimensions of a rectangular block measured with calipers having least count of 0.01 cm are 5mm$ \times $10mm$ \times $5mm. The maximum percentage error in the measurement of the volume of the block is
$\left( A \right)$ 5%
$\left( B \right)$ 10%
$\left( C \right)$ 15%
$\left( D \right)$ 20%

Answer 1

- Hint: In this apply the concept that volume of the cuboid is the multiplication of its respective length, breadth and height and later on in the solution use the concept that to find the maximum possible error in the volume calculate all the % error for the respective sides and add then so use these properties to reach the solution of the question.

Formula used – $V = l \times b \times h$, $\dfrac{{\Delta V}}{V} \times 100 = \dfrac{{\Delta l}}{l} \times 100 + \dfrac{{\Delta b}}{b} \times 100 + \dfrac{{\Delta h}}{h} \times 100$

Complete step-by-step solution -



Given data:
Least count in the measurement of the dimensions of the rectangular block (i.e. error in measurements) are, $\Delta l = \Delta b = \Delta h = 0.01$cm
Where l, b and h are the length, breadth and height of the rectangular box.
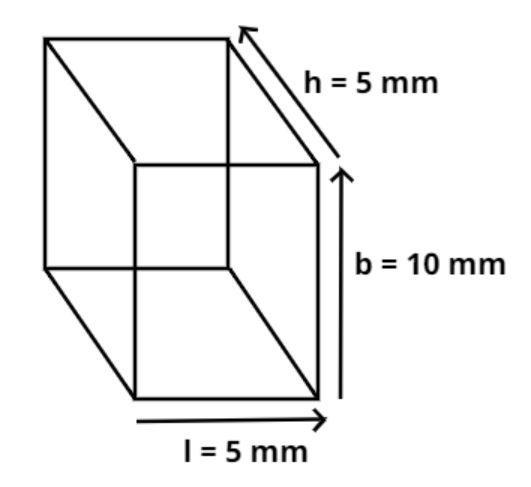
Now the given dimension of the rectangular box = 5mm$ \times $10mm$ \times $5mm
So let l = 5 mm, b = 10 mm and h = 5 mm.
Now as we know that 1 mm = 0.1 cm
Therefore l = 5mm = 0.5cm, b = 10mm = 1 cm and h = 5mm = 0.5cm.
Now as we know that the volume of the cuboid (i.e. rectangular block) = $l \times b \times h$
And the percentage error in any of its sides is the ratio of error in the respective side to length of the respective side multiplied by 100.
So the % error in the length is $\dfrac{{\Delta l}}{l} \times 100$
Similarly % error in the breadth is $\dfrac{{\Delta b}}{b} \times 100$
% error in the height is $\dfrac{{\Delta h}}{h} \times 100$
% error in the volume is $\dfrac{{\Delta V}}{V} \times 100$
So the maximum percentage error in the volume is the addition of the respective percentage error in the length, breadth and height of the rectangular block.
$ \Rightarrow \dfrac{{\Delta V}}{V} \times 100 = \dfrac{{\Delta l}}{l} \times 100 + \dfrac{{\Delta b}}{b} \times 100 + \dfrac{{\Delta h}}{h} \times 100$
Now substitute the values we have,
$ \Rightarrow \dfrac{{\Delta V}}{V} \times 100 = \dfrac{{0.01}}{{0.5}} \times 100 + \dfrac{{0.01}}{1} \times 100 + \dfrac{{0.01}}{{0.5}} \times 100$
Now simplify the above equation we have,
$ \Rightarrow \dfrac{{\Delta V}}{V} \times 100 = 2 + 1 + 2 = 5$%
So this is the required answer.
Hence option (A) is the correct answer.

Note – Whenever we face such types of questions the key concept involved here the percentage error in any of its side is the ratio of error in the respective side to length of the respective side multiplied by 100, so the maximum possible error in the volume is the sum of all the % error of the respective sides as above shown so just substitute the values and simplify, we will get the required answer.