Question

Show that the function f(x) = 2x-|x| is continuous at x = 0.

Answer 1

Hint: Use the fact that if f(x) is continuous and g(x) is continuous at x= a then so is f(x)+g(x) and f(x)g(x). In the above property take f(x) = 2x and g(x) = -|x|. Use the fact that 2x and –|x| are continuous at x = 0. Alternatively, we can prove that $\underset{x\to {{0}^{-}}}{\mathop{\text{Lim}}}\,f\left( x \right)=\underset{x\to {{0}^{+}}}{\mathop{\text{Lim}}}\,f\left( x \right)=f\left( 0 \right)$. Alternatively you can draw a graph of f(x) and verify whether f(x) is continuous at x= 0 or not.

Complete step-by-step answer:

We know that g(x) = 2x is continuous for all real x. Hence g(x) is continuous at x = 0.
Also h(x) = -|x| is continuous for all real x. Hence h(x) is also continuous at x= 0.
Hence g(x)+h(x) is also continuous at x=0.
Hence 2x-|x| is also continuous at x = 0.
Hence f(x) continuous at x=0.

Note: [1] Alternatively, we have
$\underset{x\to {{0}^{-}}}{\mathop{\text{Lim}}}\,f\left( x \right)=\underset{x\to {{0}^{-}}}{\mathop{\text{Lim}}}\,2x-\left| x \right|$
Since for x<0 |x| = -x, we get
$\underset{x\to {{0}^{-}}}{\mathop{\text{Lim}}}\,f\left( x \right)=\underset{x\to {{0}^{-}}}{\mathop{\text{Lim}}}\,2x+x=\underset{x\to {{0}^{-}}}{\mathop{\text{Lim}}}\,3x=0$
$\underset{x\to {{0}^{+}}}{\mathop{\text{Lim}}}\,f\left( x \right)=\underset{x\to {{0}^{+}}}{\mathop{\text{Lim}}}\,2x-\left| x \right|$
Since for x>0 |x| = x, we get
$\underset{x\to {{0}^{+}}}{\mathop{\text{Lim}}}\,f\left( x \right)=\underset{x\to {{0}^{+}}}{\mathop{\text{Lim}}}\,2x-x=\underset{x\to {{0}^{+}}}{\mathop{\text{Lim}}}\,x=0$
f(0) = 2(0)-|0| = 0-0 = 0.
Hence, we have $\underset{x\to {{0}^{-}}}{\mathop{\text{Lim}}}\,f\left( x \right)=\underset{x\to {{0}^{+}}}{\mathop{\text{Lim}}}\,f\left( x \right)=f\left( 0 \right)$
Hence f(x) is continuous at x = 0.
[2] Alternatively, we can draw the graph of f(x) and verify that f(x) is continuous at x = 0

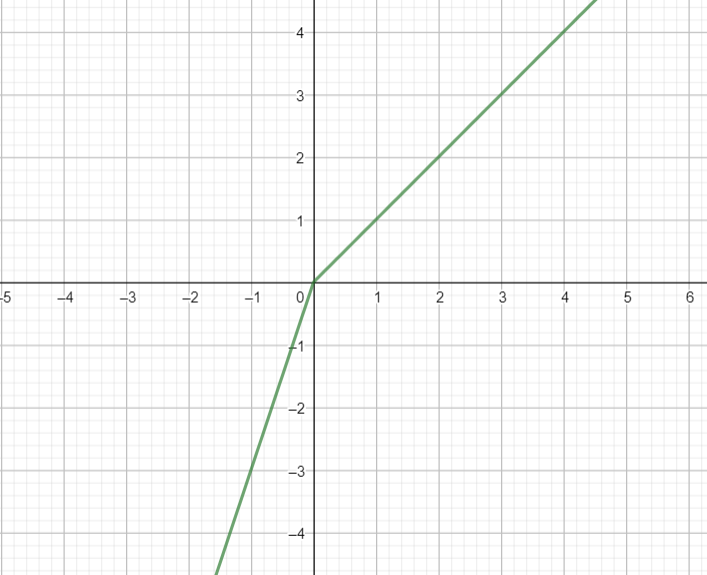
From the graph, it is clear that f(x) is continuous at x=0.