Question

Give a brief history of the mathematician Pythagoras. Verify Pythagoras theorem by paper cutting, folding and pasting.

Answer 1

Hint: We will take reference of the basic definition of Pythagoras theorem which states that in a right angled triangle, the square of the hypotenuse is equal to the sum of the square on the other two sides.

It is given in the question that we have to give a brief history of the mathematician Pythagoras and also verify the Pythagoras theorem by paper cutting, folding and pasting. Pythagoras was an ancient Ionian Greek philosopher and he is the founder of Pythagoreanism. His political religious teachings were well known in Magna Graecia and influenced Pluto and Aristotle.
We know that according to the Pythagoras theorem, in a right angled triangle, the square of the hypotenuse is equal to the sum of the squares on the other two sides, that is, ${{\left( hypotenuse \right)}^{2}}={{\left( height \right)}^{2}}+{{\left( base \right)}^{2}}$. Now, we will verify the Pythagoras theorem by an activity of paper cutting, folding and pasting. For the same, we will follow the following steps.
Step 1 : We will take a paper and draw a right angled triangle ABC right angled at C of sides 3 cm, 4 cm and 5 cm respectively. We will then cut out the triangle.

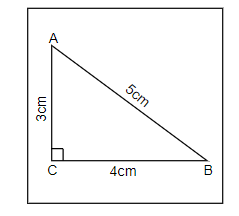
Step 2 : We will paste the cut out of the triangle on a new sheet of paper.
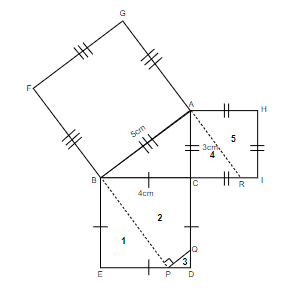
Step 3 : We will draw a square on each of the sides of triangle ABC and name them accordingly as shown in the figure below.

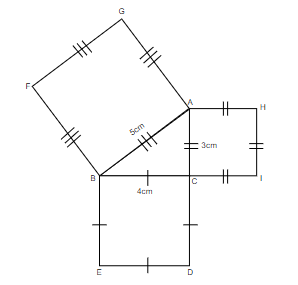
Step 4 : We will extend FB and GA of the square GFBA so that they meet ED at P and CI at R respectively, as shown below.

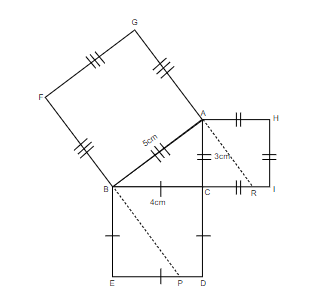
Step 5 : We will then draw a perpendicular PQ on BP

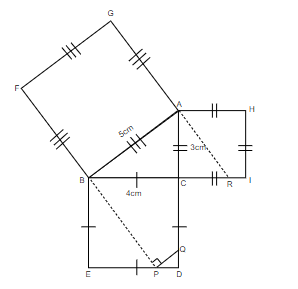
Step 6 : Now, we will name the parts of the triangles formed in the square EDCB and ACIH as 1, 2, 3, 4, and 5 respectively.

Step 7 : Now, we will cut out the numbered pieces. We will then place all these pieces of triangles on the square ABFG. So, we get the figure as,

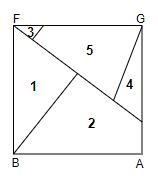
Now, let us look at the calculations. As we had cut out the pieces of the the squares EDCB and ACIH and placed them on the square ABFG, we see that they cover this square completely. We know that the area of the square is given as ${{\left( side \right)}^{2}}$. So, we can say that,
Area of square ACIH = ${{\left( AC \right)}^{2}}={{\left( 3cm \right)}^{2}}=9c{{m}^{2}}$.
Also, area of square EDCB = ${{\left( BC \right)}^{2}}={{\left( 4cm \right)}^{2}}=16c{{m}^{2}}$
 And area of square ABFG = ${{\left( AB \right)}^{2}}={{\left( 5cm \right)}^{2}}=25c{{m}^{2}}$
Thus, we get ,
$\begin{align}
  & {{\left( AB \right)}^{2}}={{\left( BC \right)}^{2}}+{{\left( AC \right)}^{2}} \\
 & \Rightarrow 25=9+16 \\
 & \Rightarrow 25=25 \\
\end{align}$
So, as LHS = RHS, it is proved.
Therefore, Pythagoras theorem is proved.

Note: Many students get confuse with the Pythagoras theorem and mix it up with the basic proportionality theorem. They may write Pythagoras theorem as the square of hypotenuse is in the same ratio of its square of height and base. But this is an incorrect concept and we should know the basic definitions and theorems. They should go step by step while trying to prove the Pythagoras theorem by paper cutting and do the calculations correctly.