
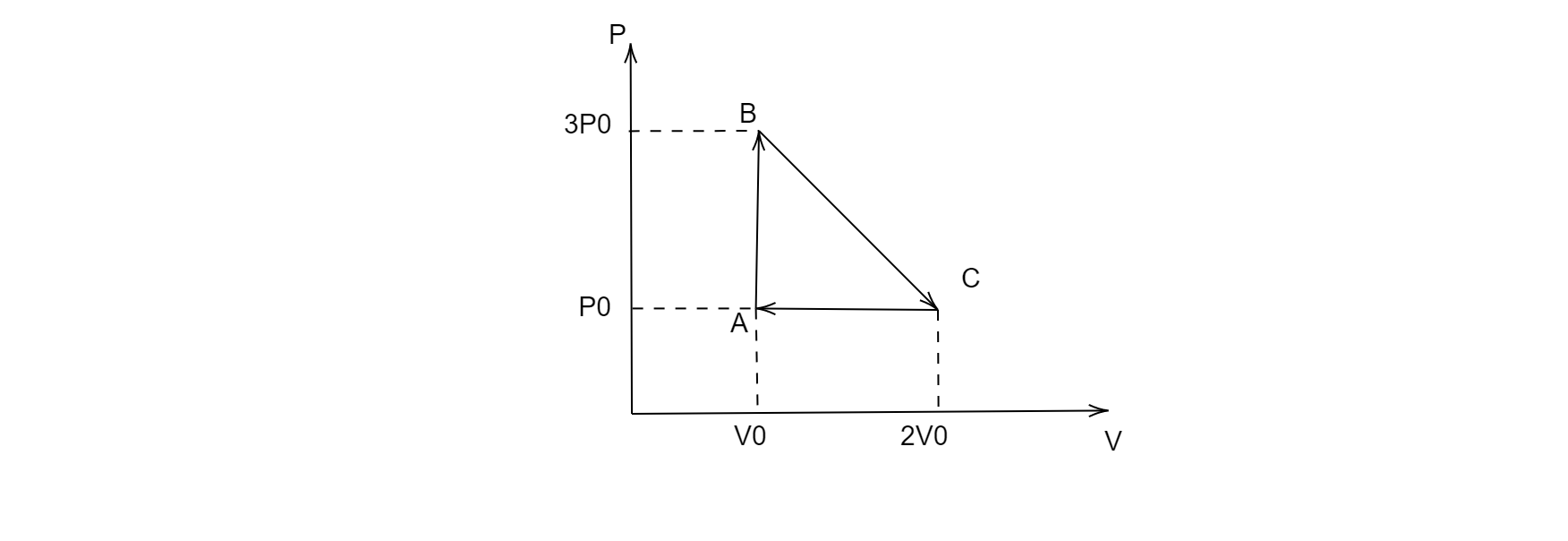
One mole of an ideal monatomic gas is taken round the cyclic process $ABCA$ as shown in the figure, calculate the heat rejected by the gas in the path $CA$ and the heat absorbed by the gas in the path $AB$.
Answer
233.1k+ views
Hint: The use of ${C_p}$ and ${C_v}$ will simplify the problem. Also, since $CA$ and $AB$ processes are isobaric and isochoric respectively, equations can be used using these two properties of the gas in the respective paths.
Complete step by step solution:
Since the gas is monatomic, therefore the value of number of moles i.e. $n$ will be $1$. The specific heat capacities at constant volume and constant pressure are:
${C_v} = \dfrac{3}{2}R$
$ \Rightarrow \dfrac{{{C_v}}}{R} = \dfrac{3}{2}$
${C_p} = \dfrac{5}{2}R$
$ \Rightarrow \dfrac{{{C_p}}}{R} = \dfrac{5}{2}$
Where ${C_p}$ and ${C_v}$ are the molar specific heat capacities of the gas at constant pressure and constant volume respectively of an ideal gas. Specific heat capacity of a substance is defined as the heat supplied per unit mass of that particular substance per unit rise in temperature.
Since the process $CA$ is isobaric i.e. the pressure remains constant throughout the process for this path, therefore the heat rejected by the gas in the path $CA$ will be:
$\Rightarrow d{h_{CA}} = {C_p}({T_{final}} - {T_{initial}})$
$\Rightarrow d{h_{CA}} = {C_p}(\dfrac{{{P_0}{V_0}}}{R} - \dfrac{{2{P_0}{V_0}}}{R})$
$\Rightarrow d{h_{CA}} = \dfrac{{{C_p}}}{R}({P_0}{V_0} - 2{P_0}{V_0})$
$\Rightarrow d{h_{CA}} = \dfrac{5}{2}({P_0}{V_0} - 2{P_0}{V_0})$
Where $d{h_{CA}}$ is the heat rejected during the process.
$\Rightarrow d{h_{CA}} = - \dfrac{5}{2}({P_0}{V_0})$
Since the process $AB$ is isochoric, i.e. the volume remains constant throughout the process for this path, therefore the heat rejected by the gas in the path $AB$ will be:
$\Rightarrow d{h_{AB}} = {C_v}dT$
Where $d{h_{AB}}$ is the heat absorbed by the monatomic gas in the process $AB$.
$\Rightarrow d{h_{AB}} = {C_v}({T_{final}} - {T_{initial}})$
$\Rightarrow {C_v}(\dfrac{{{P_f}{V_f}}}{R} - \dfrac{{{P_i}{V_i}}}{R})$
$ \Rightarrow \dfrac{{{C_v}}}{R}({P_f}{V_f} - {P_i}{V_i})$
$\Rightarrow \dfrac{3}{2}({P_f}{V_f} - {P_i}{V_i})$
$ \Rightarrow \dfrac{3}{2}(3{P_0}{V_0} - {P_0}{V_0})$
$ \Rightarrow 3{P_0}{V_0}$
Therefore, the heat rejected by the gas in the path $CA$ is $ - \dfrac{5}{2}({P_0}{V_0})$ and the heat absorbed by the gas in the path $AB$ is $3{P_0}{V_0}$.
Note: If the heat rejected in the path $CA$ is negative, then this implies that no heat is rejected in this process but there is heat absorption in the process. In the process $AB$ no such negative sign is encountered therefore the process has absorbed heat.
Complete step by step solution:
Since the gas is monatomic, therefore the value of number of moles i.e. $n$ will be $1$. The specific heat capacities at constant volume and constant pressure are:
${C_v} = \dfrac{3}{2}R$
$ \Rightarrow \dfrac{{{C_v}}}{R} = \dfrac{3}{2}$
${C_p} = \dfrac{5}{2}R$
$ \Rightarrow \dfrac{{{C_p}}}{R} = \dfrac{5}{2}$
Where ${C_p}$ and ${C_v}$ are the molar specific heat capacities of the gas at constant pressure and constant volume respectively of an ideal gas. Specific heat capacity of a substance is defined as the heat supplied per unit mass of that particular substance per unit rise in temperature.
Since the process $CA$ is isobaric i.e. the pressure remains constant throughout the process for this path, therefore the heat rejected by the gas in the path $CA$ will be:
$\Rightarrow d{h_{CA}} = {C_p}({T_{final}} - {T_{initial}})$
$\Rightarrow d{h_{CA}} = {C_p}(\dfrac{{{P_0}{V_0}}}{R} - \dfrac{{2{P_0}{V_0}}}{R})$
$\Rightarrow d{h_{CA}} = \dfrac{{{C_p}}}{R}({P_0}{V_0} - 2{P_0}{V_0})$
$\Rightarrow d{h_{CA}} = \dfrac{5}{2}({P_0}{V_0} - 2{P_0}{V_0})$
Where $d{h_{CA}}$ is the heat rejected during the process.
$\Rightarrow d{h_{CA}} = - \dfrac{5}{2}({P_0}{V_0})$
Since the process $AB$ is isochoric, i.e. the volume remains constant throughout the process for this path, therefore the heat rejected by the gas in the path $AB$ will be:
$\Rightarrow d{h_{AB}} = {C_v}dT$
Where $d{h_{AB}}$ is the heat absorbed by the monatomic gas in the process $AB$.
$\Rightarrow d{h_{AB}} = {C_v}({T_{final}} - {T_{initial}})$
$\Rightarrow {C_v}(\dfrac{{{P_f}{V_f}}}{R} - \dfrac{{{P_i}{V_i}}}{R})$
$ \Rightarrow \dfrac{{{C_v}}}{R}({P_f}{V_f} - {P_i}{V_i})$
$\Rightarrow \dfrac{3}{2}({P_f}{V_f} - {P_i}{V_i})$
$ \Rightarrow \dfrac{3}{2}(3{P_0}{V_0} - {P_0}{V_0})$
$ \Rightarrow 3{P_0}{V_0}$
Therefore, the heat rejected by the gas in the path $CA$ is $ - \dfrac{5}{2}({P_0}{V_0})$ and the heat absorbed by the gas in the path $AB$ is $3{P_0}{V_0}$.
Note: If the heat rejected in the path $CA$ is negative, then this implies that no heat is rejected in this process but there is heat absorption in the process. In the process $AB$ no such negative sign is encountered therefore the process has absorbed heat.
Recently Updated Pages
JEE Main 2023 April 6 Shift 1 Question Paper with Answer Key

JEE Main 2023 April 6 Shift 2 Question Paper with Answer Key

JEE Main 2023 (January 31 Evening Shift) Question Paper with Solutions [PDF]

JEE Main 2023 January 30 Shift 2 Question Paper with Answer Key

JEE Main 2023 January 25 Shift 1 Question Paper with Answer Key

JEE Main 2023 January 24 Shift 2 Question Paper with Answer Key

Trending doubts
JEE Main 2026: Session 2 Registration Open, City Intimation Slip, Exam Dates, Syllabus & Eligibility

JEE Main 2026 Application Login: Direct Link, Registration, Form Fill, and Steps

JEE Main Marking Scheme 2026- Paper-Wise Marks Distribution and Negative Marking Details

Understanding the Angle of Deviation in a Prism

Hybridisation in Chemistry – Concept, Types & Applications

How to Convert a Galvanometer into an Ammeter or Voltmeter

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Laws of Motion Class 11 Physics Chapter 4 CBSE Notes - 2025-26

Waves Class 11 Physics Chapter 14 CBSE Notes - 2025-26

Mechanical Properties of Fluids Class 11 Physics Chapter 9 CBSE Notes - 2025-26

Thermodynamics Class 11 Physics Chapter 11 CBSE Notes - 2025-26

Units And Measurements Class 11 Physics Chapter 1 CBSE Notes - 2025-26




