Question

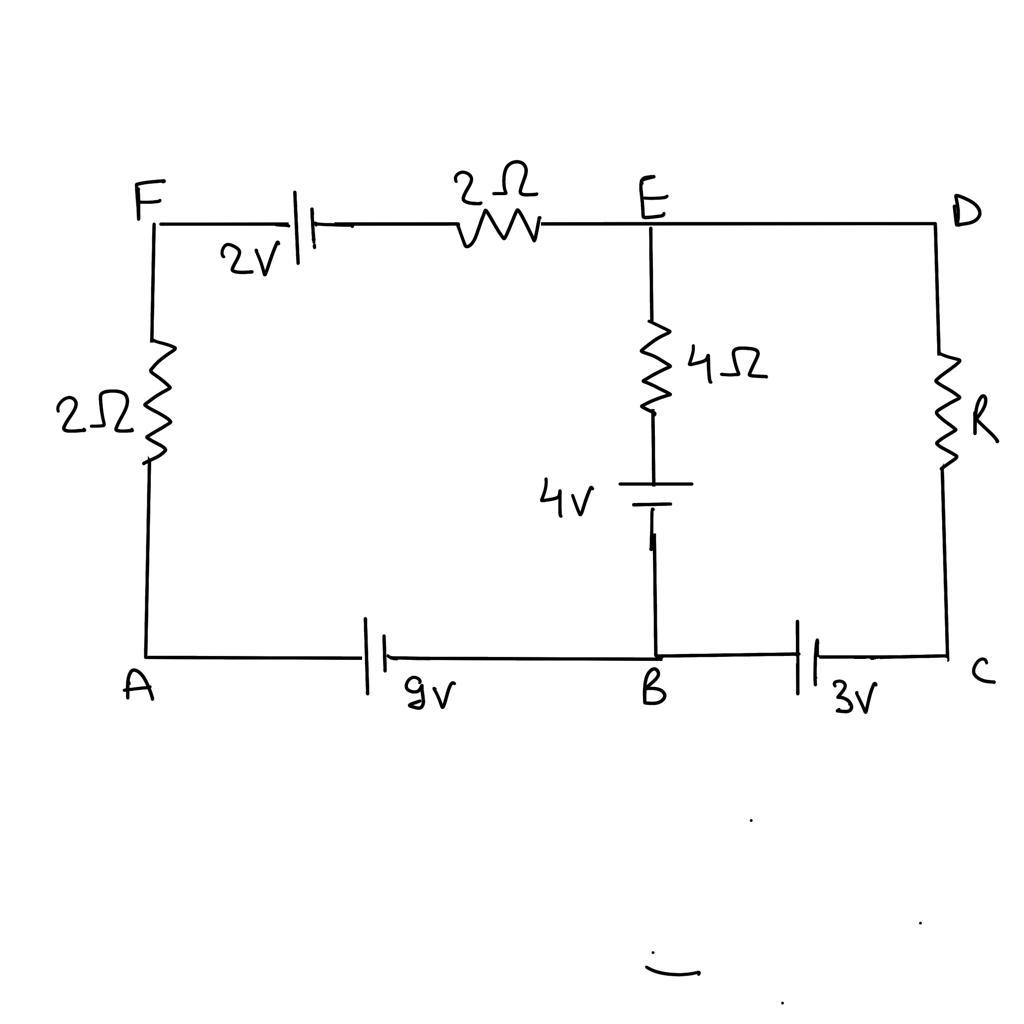
In the electric network shown, when no current flows through the 4$\Omega $ resistor in the arm EB the potential difference between the points A and D will be,

$A.$ 5V
$B.$ 3V
$C.$ 4V
$D.$ 6V

Answer 1

HINT- In series and parallel combination we have to keep in mind that current is same in series combination while the voltage is same in parallel combination. Potential difference is the difference in the amount of energy that charge carriers have between two points in a circuit. It is measured in volts (V) and is also called voltage.

Complete step-by-step answer:
Now from the question, we have
Let the potential of point B = 0
Therefore, the potential of point A and C will be 9V and 3V respectively.
Distributing current across the circuit as shown in figure and applying Kirchhoff law at junction E .

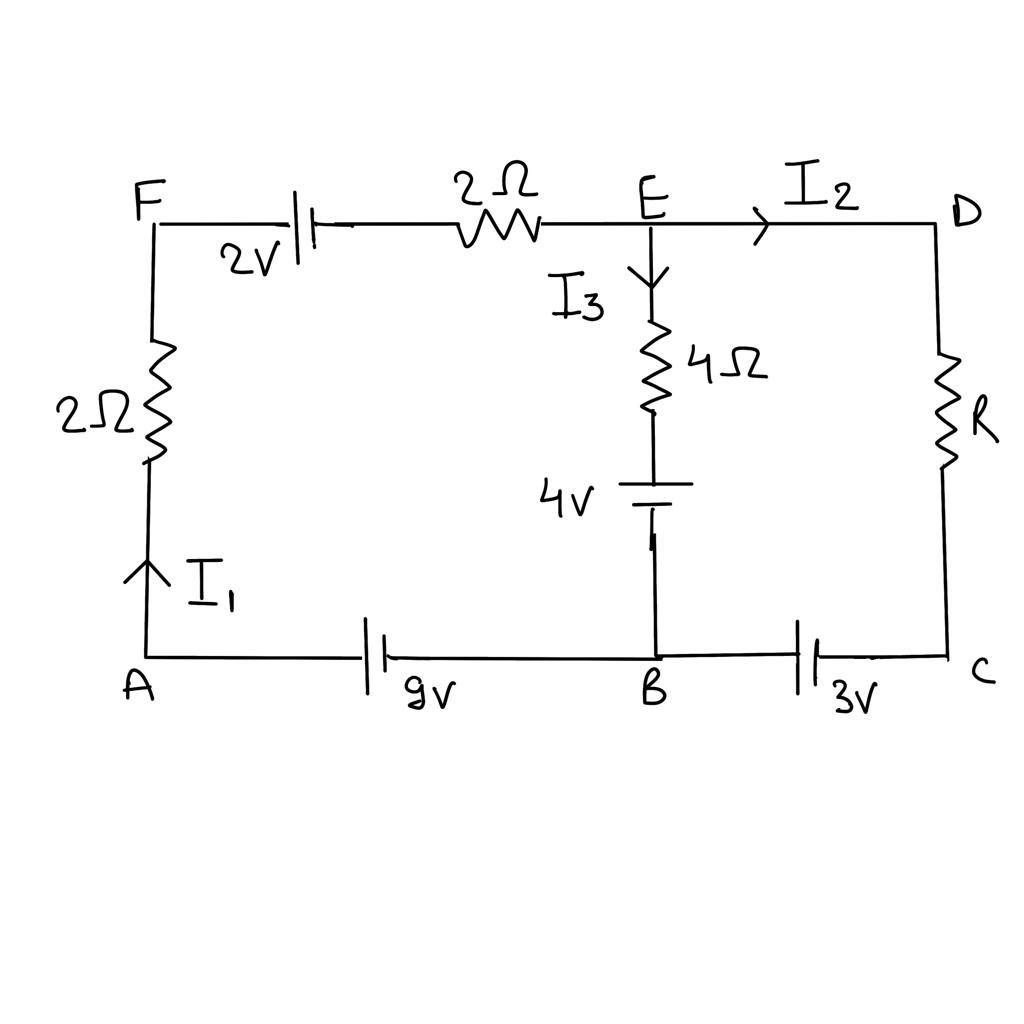
${I_1} = {I_3} + {I_2}$
As, ${I_3} = 0$ (since, there is no potential difference across EB)
Therefore, ${I_1} = {I_2}$
Also as ${I_3} = 0$
${V_E} = {V_B} + 4 = 4volts$
${V_E} = {V_D} = 4volts$
Therefore, potential difference between point A and D will be
= ${V_A} - {V_D}$
= (9-4) volts
= 5volts = 5V
Therefore, the correct option for the above question is option $A.$

NOTE- Kirchhoff’s laws
Kirchhoff’s circuit laws are two equalities that deal with the current and potential difference in the lumped electric model of electric circuits.
Kirchhoff’s current law- This is also called Kirchhoff’s first law, Kirchhoff’s point rule. This law states that, for any node (junction) in an electrical circuit, the sum of currents flowing into that node is equal to the sum of currents flowing out of that node; or equivalently. $\sum\limits_{k = 1}^n {{I_k}} = 0$, where n is the total number of branches with currents flowing towards or away from the node.
Kirchhoff’s voltage law- This law is also called Kirchhoff’s second law, Kirchhoff’s loop rule, and Kirchhoff’s second rule. This law states that the directed sum of the potential differences (voltages) around any closed loop is zero. $\sum\limits_{k = 1}^n {{V_k}} = 0$, here n is the total number of voltages measured.