Question

In an AC circuit, the resistance $R=0.2\Omega $. At a certain instant, ${{V}_{A}}-{{V}_{B}}=0.5V,I=0.5A$, and the current is increasing at the rate of $\dfrac{\Delta I}{\Delta t}=8A{{s}^{-1}}$. The inductance of the coil is:

$A)0.05H$
$B)0.1H$
$C)0.2H$
$D)$none of these

Answer 1

Hint: The given potential difference is used to calculate $emf$of the coil. This is done by determining the potentials of the coil and the resistor separately. From this determined value of induced $emf$, the inductance of the coil can be easily found out.
Formula used:
$1)V=IR$
where
$V$ is the voltage across a resistor
$I$ is the current through the resistor
$R$ is the resistance of the resistor
$2)emf=L\dfrac{dI}{dt}$
where
$emf$ is the potential induced in a coil
$\dfrac{dI}{dt}$ is the rate of change of current in the coil
$L$ is the inductance of the coil

Complete step-by-step solution:
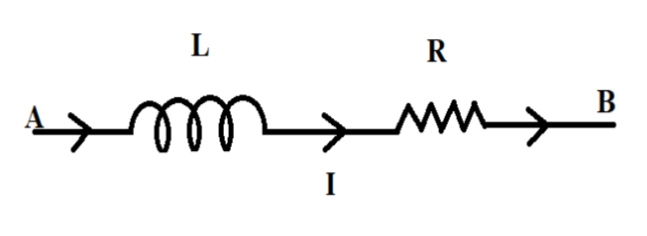
The given diagram consists of a coil and a resistor. We are provided that the potential difference between point $A$ and point $B$ is equal to the difference in potentials between the resistor and the coil. The potential of the coil is nothing but the $emf$ induced in the coil due to the flow of current. At the same time, the potential of the resistor is nothing but the product of the current flowing through the resistor and the value of resistance of the resistor (Ohm’s law). Putting all these facts mathematically, we have:
${{V}_{A}}-{{V}_{B}}={{V}_{coil}}-{{V}_{resistor}}=em{{f}_{coil}}-IR$
Let this be equation 1.
Here,
${{V}_{A}}={{V}_{coil}}=em{{f}_{coil}}$ is the induced $emf$ of the coil
and
${{V}_{B}}={{V}_{resistor}}=IR$ is the voltage across the resistor
The following diagram explains the same.

We are given that ${{V}_{A}}-{{V}_{B}}=0.5V;I=0.5A$ and $R=0.2\Omega $
Substituting these values in equation 1. We have
${{V}_{A}}-{{V}_{B}}=0.5\Rightarrow em{{f}_{coil}}-IR=0.5\Rightarrow em{{f}_{coil}}-(0.5A\times 0.2\Omega)=0.5V\Rightarrow em{{f}_{coil}}=0.6V$
Let this be equation 2.
From equation 2, it is clear that the $emf$induced in the coil is equal to $0.6V$.
Now, we know that $emf$ induced in a coil is related to the inductance of the coil by the relation:
$em{{f}_{coil}}=L\dfrac{\Delta I}{\Delta t}$
where
$em{{f}_{coil}}$ is the potential induced in the coil
$\dfrac{\Delta I}{\Delta t}$ is the rate of change of current in the coil
$L$ is the inductance of the coil
Let this be equation 3.
From the question, we know that the rate of change of current is given by
$\dfrac{\Delta I}{\Delta t}=8A{{s}^{-1}}$
Substituting this value and the value of $emf$ from equation 2, in equation 3, we have
$em{{f}_{coil}}=L\dfrac{\Delta I}{\Delta t}\Rightarrow 0.6V=L\times 8A{{s}^{-1}}\Rightarrow L=\dfrac{0.6V}{8A{{s}^{-1}}}=0.075Vs{{A}^{-1}}=0.075H$
Therefore, the inductance of the coil is given by
$L=0.075H$
Since this answer is not provided in the options, the correct option to be marked is D.

Note: Students need to understand that the inductance of a coil is nothing but the self-inductance of the coil. Self-inductance of a coil is said to be $1H$ when a current change at the rate of $1A{{s}^{-1}}$ through the coil induces and $emf$ of $1V$ in the coil. Mathematically,
$1H=\dfrac{1V}{1A{{s}^{-1}}}=1Vs{{A}^{-1}}$