Question

If \[PQ\] be a normal chord of the parabola and \[S\] be the focus, prove that the locus of the centroid of the triangle \[SPQ\] is the curve \[36a{{y}^{2}}\left( 3x-5a \right)-81{{y}^{4}}=128{{a}^{4}}\].

Answer 1

Hint: If two points \[\left( at_{1}^{2},2a{{t}_{1}} \right)\] and \[\left( at_{2}^{2},2a{{t}_{2}} \right)\] lie on a chord which is normal to the point with parameter \[{{t}_{1}}\], then , \[{{t}_{2}}=-{{t}_{1}}-\dfrac{2}{{{t}_{1}}}\]

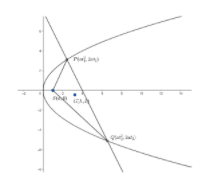
We will consider the equation of parabola be \[{{y}^{2}}=4ax\].
So , the focus of the parabola is \[S\left( a,0 \right)\].
Now, we will consider a point \[P\left( at_{1}^{2},2a{{t}_{1}} \right)\] on the parabola.
We need to find the equation of normal at this point.
We know , the equation of normal at the point \[(a{{t}^{2}},2at)\] is given as \[y=-tx+2at+a{{t}^{3}}\], where \[t\] is a parameter.
So , the equation of normal to the parabola at \[P\left( at_{1}^{2},2a{{t}_{1}} \right)\] is given as
\[y=-{{t}_{1}}x+2a{{t}_{1}}+at_{1}^{3}....\left( i \right)\]
In the question , it is given this normal is also a chord and cuts the parabola at \[Q\].
So , let the coordinates of \[Q=\left( at_{2}^{2},2a{{t}_{2}} \right)\].
\[Q\] lies on the normal chord. So , it should satisfy the equation \[\left( i \right)\].
Also, we know if two point \[\left( at_{1}^{2},2a{{t}_{1}} \right)\] and \[\left( at_{2}^{2},2a{{t}_{2}} \right)\] lie on a normal chord, then,
\[{{t}_{2}}=-{{t}_{1}}-\dfrac{2}{{{t}_{1}}}\]
So, \[Q=\left( a{{\left( {{t}_{1}}+\dfrac{2}{{{t}_{1}}} \right)}^{2}},-2a\left( {{t}_{1}}+\dfrac{2}{{{t}_{1}}} \right) \right)\]
Now, we need to find the locus of the centroid . So , let the centroid be \[G\left( h,k \right)\].
Now , we know the centroid of a triangle formed by the points \[({{x}_{1}},{{y}_{1}}),({{x}_{2}},{{y}_{2}})\] and \[({{x}_{3}},{{y}_{3}})\] is given by
\[\left( \dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3},\dfrac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3} \right)\].
Now, since \[G\] is the centroid of triangle \[SPQ\], so
\[(h,k)=\left( \dfrac{a+at_{1}^{2}+a{{\left( {{t}_{1}}+\dfrac{2}{{{t}_{1}}} \right)}^{2}}}{3},\dfrac{0+2a{{t}_{1}}-2a\left( {{t}_{1}}+\dfrac{2}{{{t}_{1}}} \right)}{3} \right)\]
Now , we will equate the coordinates .
On equating the coordinates , we get
\[h=\dfrac{a+at_{1}^{2}+a{{\left( {{t}_{1}}+\dfrac{2}{{{t}_{1}}} \right)}^{2}}}{3}.....\left( ii \right)\]
and \[k=\dfrac{0+2a{{t}_{1}}-2a\left( {{t}_{1}}+\dfrac{2}{{{t}_{1}}} \right)}{3}.....\left( iii \right)\]
From equation \[\left( iii \right)\], we get
\[3k=2a{{t}_{1}}-2a{{t}_{1}}-\dfrac{4a}{{{t}_{1}}}\]
or, \[k=\dfrac{-4a}{3{{t}_{1}}}\]
\[\Rightarrow {{t}_{1}}=\dfrac{-4a}{3k}\]
Now , we will substitute this value of \[{{t}_{1}}\] in equation \[\left( ii \right)\].
On , substituting this value of \[{{t}_{1}}\] in equation \[\left( ii \right)\] we get,
\[h=\dfrac{a+a{{\left( \dfrac{-4a}{3k} \right)}^{2}}+a{{\left( \dfrac{-4a}{3k}+\dfrac{2}{\dfrac{-4a}{3k}} \right)}^{2}}}{3}\]
\[\Rightarrow h=\dfrac{a+\dfrac{16{{a}^{3}}}{9{{k}^{2}}}+a\left( \dfrac{16{{a}^{2}}}{9{{k}^{2}}}+\dfrac{36{{k}^{2}}}{16{{a}^{2}}}+4 \right)}{3}\]
\[\Rightarrow 3h=\dfrac{9a{{k}^{2}}+16{{a}^{3}}+9a{{k}^{2}}\left( \dfrac{16{{a}^{2}}}{9{{k}^{2}}}+\dfrac{36{{k}^{2}}}{16{{a}^{2}}}+4 \right)}{9{{k}^{2}}}\]
\[\Rightarrow 3h=\dfrac{9a{{k}^{2}}+16{{a}^{3}}+16{{a}^{3}}+\dfrac{81{{k}^{4}}}{4a}+36a{{k}^{2}}}{9{{k}^{2}}}\]
\[\Rightarrow 27{{k}^{2}}h=45a{{k}^{2}}+32{{a}^{3}}+\dfrac{81{{k}^{4}}}{4a}\]
\[\Rightarrow 108a{{k}^{2}}h=180{{a}^{2}}{{k}^{2}}+128{{a}^{4}}+81{{k}^{4}}\]
\[\Rightarrow 36a{{k}^{2}}\left( 3h-5a \right)-81{{k}^{4}}=128{{a}^{4}}.........\]equation\[\left( iv \right)\]
So , the locus of \[G\left( h,k \right)\] is given by replacing \[\left( h,k \right)\] by \[(x,y)\] in equation \[\left( iv \right)\]
So, the equation of locus of the centroid is \[36a{{y}^{2}}\left( 3x-5a \right)-81{{y}^{4}}=128{{a}^{4}}\]

Note: While simplifying the equations , please make sure that sign mistakes do not occur. These mistakes are very common and can cause confusions while solving. Ultimately the answer becomes wrong. So, sign conventions should be carefully taken .