Question

If $f\left( xy \right)=f\left( x \right)+f\left( y \right)\forall x,y\ne 0\And f'\left( 1 \right)=3,$then test the differentiability of $f\left( x \right)$.

Answer 1

Hint: Since we have to test the differentiability, we have to find the derivative of the function. We can find derivatives using first principles and using the functional relation given in the question.

 It is given in the question $f\left( xy \right)=f\left( x \right)+f\left( y \right)\forall x,y\ne 0\text{ }\And f'\left( 1 \right)=3,$
To check differentiability, we have to find $f'\left( x \right)$. To find $f'\left( x \right)$ we have to follow certain no. of steps,
1. Use first principle to find $f'\left( x \right)$
We know by first principle,
$\begin{align}
  & f'\left( x \right)=\underset{h\to 0}{\mathop{\lim }}\,\dfrac{f\left( x+h \right)-f\left( x \right)}{h} \\
 & \Rightarrow f'\left( x \right)=\underset{h\to 0}{\mathop{\lim }}\,\dfrac{f\left( x\left( 1+\dfrac{h}{x} \right) \right)-f\left( x \right)}{h}.........\left( I \right) \\
\end{align}$
Since it is given $f\left( xy \right)=f\left( x \right)+f\left( y \right)$, we can substitute $f\left( x\left( 1+\dfrac{h}{x} \right) \right)=f\left( x \right)+f\left( 1+\dfrac{h}{x} \right)$ in $\left( I \right)$,
$\begin{align}
  & \Rightarrow f'\left( x \right)=\underset{h\to 0}{\mathop{\lim }}\,\dfrac{f\left( x \right)+f\left( 1+\dfrac{h}{x} \right)-f\left( x \right)}{h} \\
 & \Rightarrow f'\left( x \right)=\underset{h\to 0}{\mathop{\lim }}\,\dfrac{f\left( 1+\dfrac{h}{x} \right)}{h} \\
\end{align}$
Now, we cannot proceed further in step 1. So, we proceed to step 2.
2. We will find some boundary values of $f\left( x \right)$.
Given $f\left( xy \right)=f\left( x \right)+f\left( y \right)$
Substituting $x=1,y=1$ in the above functional relation, we get 🡪
$\begin{align}
  & f\left( 1 \right)=f\left( 1 \right)+f\left( 1 \right) \\
 & \Rightarrow f\left( 1 \right)=2f\left( 1 \right) \\
 & \Rightarrow f\left( 1 \right)=0......................\left( II \right) \\
\end{align}$
Now we will go to step 1. Adding/subtracting $0$to any term will not cause any change in value.
So, in the final expression of step1, we will do the following changes,
$f'\left( x \right)=\underset{h\to 0}{\mathop{\lim }}\,\dfrac{f\left( 1+\dfrac{h}{x} \right)-0}{h}$

Now, we will multiple and divide the denominator with $x$. Also, from $\left( II \right)$, we can substitute 0 as f1.
$f'\left( x \right)=\underset{h\to 0}{\mathop{\lim }}\,\dfrac{f\left( 1+\dfrac{h}{x} \right)-f\left( 1 \right)}{x.\dfrac{h}{x}}$
Since limit is of $h$, we can take $\dfrac{1}{x}$ out of the limit.
$f'\left( x \right)=\dfrac{1}{x}\underset{h\to 0}{\mathop{\lim }}\,\dfrac{f\left( 1+\dfrac{h}{x} \right)-f\left( 1 \right)}{\dfrac{h}{x}}$
Since it is given $x\ne 0,$ we can replace $\underset{h\to 0}{\mathop{\lim }}\,\text{ by }\underset{\dfrac{h}{x}\to 0}{\mathop{\lim }}\,$
$f'\left( x \right)=\dfrac{1}{x}\underset{\dfrac{h}{x}\to 0}{\mathop{\lim }}\,\dfrac{f\left( 1+\dfrac{h}{x} \right)-f\left( 1 \right)}{\dfrac{h}{x}}...........\left( III \right)$
If we substitute $x=1$ in the first principle of derivative, we will get,
$\begin{align}
  & f'\left( x \right)=\underset{h\to 0}{\mathop{\lim }}\,\dfrac{f\left( x+h \right)-f\left( x \right)}{h} \\
 & x=1\to \\
 & \Rightarrow f'\left( x \right)=\underset{h\to 0}{\mathop{\lim }}\,\dfrac{f\left( 1+h \right)-f\left( 1 \right)}{h}.........\left( IV \right) \\
\end{align}$
In $\left( IV \right)$, we can write $\underset{h\to 0}{\mathop{\lim }}\,\dfrac{f\left( 1+h \right)-f\left( 1 \right)}{h}=f'\left( 1 \right)$
Similarly, in $\left( III \right)$, we can write
\[\underset{\dfrac{h}{x}\to 0}{\mathop{\lim }}\,\dfrac{f\left( 1+\dfrac{h}{x} \right)-f\left( 1 \right)}{\dfrac{h}{x}}=f'\left( 1 \right)\]
So, substituting in $\left( III \right)$, we get,
\[f'\left( x \right)=\dfrac{1}{x}\times of'\left( 1 \right)\]
It is given \[f'\left( 1 \right)=3\],
$\Rightarrow f'\left( x \right)=\dfrac{3}{x}$
If we draw the graph of $f'\left( x \right)=\dfrac{3}{x}$, we get 🡪

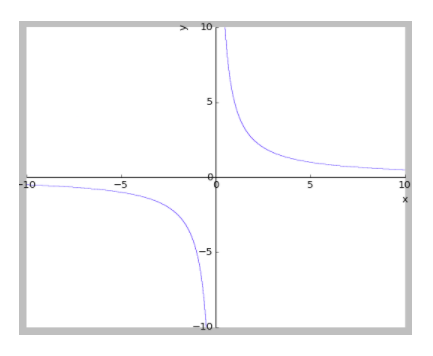
This graph is not continuous at $x=0$ since $\underset{x\to {{0}^{-}}}{\mathop{\lim }}\,f'\left( x \right)\ne \underset{x\to {{0}^{+}}}{\mathop{\lim }}\,f'\left( x \right)$.
So we can say that $f\left( x \right)$ is differentiable $\ for all x\in R-\left\{ 0 \right\}$.

Note: There is a possibility of mistake while finding the boundary value of the function in step 2. The boundary value is to be found by taking help of the information given in the question. For example, it was given in the question that $f'\left( 1 \right)=3$ that is why we found the value of $f\left( 1 \right)$ in step 2.