Question

If \[{C_1} = 20\mu F,\;{C_2} = 30\mu F\;and\;{C_3} = 15\mu F\] and the insulated plate of $C{}_1$ is at a potential of $90 V$, one plate of ${C_3}$ being earthed. What is the potential difference between the plates of ${C_2}$ and the three capacitors being connected in series?

Answer 1

Hint: Capacitors are the electronic component which stores energy. It has the ability to store energy in the form of an electrical charge across the terminals producing the potential difference. When the capacitors are connected one after the other, such an arrangement is known as the capacitors are in series and its capacitance can be found by adding the reciprocals of all the given capacitors in the series.

Complete step by step answer:

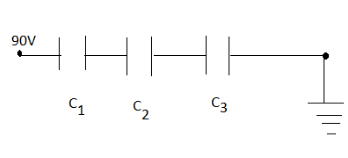
Given that- the three capacitors are connected with each other in the series as shown in the above figure.
Now, Equivalence of the capacitors is –
\[\Rightarrow\dfrac{1}{{{C_{eq}}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}} + \dfrac{1}{{{C_3}}}\]
Since the given values of all the three capacitors are in the same system of units, so place the values directly in the above equation-
\[\Rightarrow\dfrac{1}{{{C_{eq}}}} = \dfrac{1}{{20}} + \dfrac{1}{{30}} + \dfrac{1}{{15}}\]
Simplify the above equation – Take LCM (Least Common Multiple)
 \[\
\Rightarrow \dfrac{1}{{{C_{eq}}}} = \dfrac{3}{{60}} + \dfrac{2}{{60}} + \dfrac{4}{{60}} \\
\Rightarrow \dfrac{1}{{{C_{eq}}}} = \dfrac{9}{{60}} \\
\Rightarrow \dfrac{1}{{{C_{eq}}}} = \dfrac{3}{{20}} \\
\Rightarrow {C_{eq}} = \dfrac{{20}}{3}\mu F \\
\ \]
Now, given that potential at ${C_1} = 90V$ and ${C_3}$ being earthed, $V = 0$
Therefore, the charge $q = {C_{eq}} \times V$
Place values in the above equation – Here convert microfarad into Farad and then place it.
\[\
\Rightarrow q = \dfrac{{20}}{3} \times {10^{ - 6}} \times 90 \\
\Rightarrow q = 600 \times {10^{ - 6}} \\
\Rightarrow q = 600 \times {10^{ - 4}}c \\
\ \]
Therefore we have the charge across all the three capacitors.
Now, potential difference across the ${C_2}$ is –
$\Rightarrow {V_2} = \dfrac{q}{{{C_2}}}$
Place the values in the above equations and simplify –
$\Rightarrow {V_2} = \dfrac{{6 \times {{10}^{ - 4}}}}{{30 \times {{10}^{ - 6}}}}$
When the exponent has the same base and in the form of division, the powers are subtracted. Here the power in the denominator is negative; therefore the negative into negative becomes positive.
$
\Rightarrow {V_2} = \dfrac{{6 \times {{10}^{ - 4 + 6}}}}{{30}} \\
\Rightarrow {V_2} = \dfrac{{6 \times 100}}{{30}} \\
\Rightarrow {V_2} = 20V \\
$
Hence, the required answer - The potential difference between the plates of ${C_2}$ and the three capacitors being connected in series is $90V$.

Note: Always check the given units for all the terms when you substitute its value for the simplification. Always double check the units, and accordingly convert all the values in the same system of units. Remember basic conversational relations for the substitution. Like meter and centimeter relation and like that many more.