
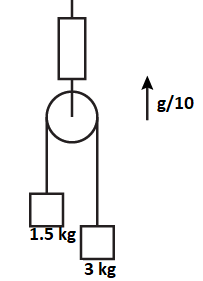
Find the reading of the spring balance shown in figure. The elevator is going up with an acceleration of g/10, the pulley and the string are light and the pulley is smooth.
Answer
233.1k+ views
Hint: For every pulley and the string system question, try to draw a free body diagram (FBD) for the given situation and then with the help of FBD, write relevant equations involving all the forces acting on the body and solve them.
Complete step by step solution:
Given that the elevator is going up with an acceleration of g/10.
Free body diagram (FBD) is a diagram showing all forces acting on a body using arrows, considering body as a point mass.
FBD of the given situation is shown below:
Tension (T): It is an internal molecular force which appear in a string when it is taunt by some external force. Force of tension always acts along the length of the string. Force of tension always act along the length of the string. Direction of tension is always away from the tied ends or points of contact of string. It always has pulling tendency.
Here, $\dfrac{{{{{m}}_{{A}}}{{g}}}}{{{{10}}}}$ and $\dfrac{{{{{m}}_{{B}}}{{g}}}}{{{{10}}}}$are pseudo force.
Let us consider that mass of body A is 3 kg and mass of body B is 1.5 kg (as per given figure)
For body A
${{{m}}_{{A}}}{{a = T - }}{{{m}}_{{A}}}{{g - }}\dfrac{{{{{m}}_{{A}}}{{g}}}}{{{{10}}}}...{{(i)}}$
For body B
${{{m}}_{{B}}}{{a = }}{{{m}}_{{B}}}{{g + }}\dfrac{{{{{m}}_{{B}}}{{g}}}}{{{{10}}}}{{ - T}}...{{(ii)}}$
Adding equations (i) and (ii), we get
$
{{{m}}_{{A}}}{{a + }}{{{m}}_{{B}}}{{a = T - }}{{{m}}_{{A}}}{{g - }}\dfrac{{{{{m}}_{{A}}}{{g}}}}{{{{10}}}}{{ + }}{{{m}}_{{B}}}{{g + }}\dfrac{{{{{m}}_{{B}}}{{g}}}}{{{{10}}}}{{ - T}} \\
\Rightarrow {{(}}{{{m}}_{{A}}}{{ + }}{{{m}}_{{B}}}{{)a = (}}{{{m}}_{{B}}}{{ - }}{{{m}}_{{A}}}{{)g + (}}{{{m}}_{{B}}}{{ - }}{{{m}}_{{A}}}{{)}}\dfrac{{{g}}}{{{{10}}}} \\
$
As ${{{m}}_{{A}}}{{ = 1}}{{.5 kg}}$ and ${{{m}}_{{B}}}{{ = 3 kg}}$
On substituting the values of masses ${{{m}}_{{A}}}$and ${{{m}}_{{B}}}$in above equation, we get
$
{{(1}}{{.5 + 3)a = (3 - 1}}{{.5)g + (3 - 1}}{{.5)}}\dfrac{{{g}}}{{{{10}}}} \\
\Rightarrow 4.{{5a = 1}}{{.5g - 1}}{{.5}}\dfrac{{{g}}}{{{{10}}}} \\
\Rightarrow {{4}}{{.5a = 1}}{{.5g}}\left( {{{1 - }}\dfrac{{{1}}}{{{{10}}}}} \right) \\
\Rightarrow {{4}}{{.5a = 1}}{{.5g \times }}\dfrac{{{9}}}{{{{10}}}} \\
\therefore \dfrac{{{a}}}{{{g}}}{{ = }}\dfrac{{{3}}}{{{{10}}}} \\
$
Now using equation (i), we get
$
{{{m}}_{{A}}}{{a = T - }}{{{m}}_{{A}}}{{g - }}\dfrac{{{{{m}}_{{A}}}{{g}}}}{{{{10}}}} \\
{{Or }} \\ T= {{{m}}_{{A}}}{{(a + g + }}\dfrac{{{g}}}{{{{10}}}}{{)}} \\
$
Reading of the spring balance is given by
$
\dfrac{{{{2T}}}}{{{g}}}{{ = }}\dfrac{{{2}}}{{{g}}}{{{m}}_{{A}}}{{(a + g + }}\dfrac{{{g}}}{{{{10}}}}{{)}} \\
{{Or }} \\ \dfrac{{{{2T}}}}{{{g}}}{{ = 2 \times 1}}{{.5}}\left( {\dfrac{{{a}}}{{{g}}}{{ + 1 + }}\dfrac{{{1}}}{{{{10}}}}} \right) \\
\Rightarrow {{3}}\left( {\dfrac{{{3}}}{{{{10}}}}{{ + 1 + }}\dfrac{{{1}}}{{{{10}}}}} \right){{ = 3(0}}{{.3 + 1 + 0}}{{.1) = 4}}{{.2 Kg}} \\
$
The reading of the spring balance will be 4.2 Kg.
Note: In free body diagram, we draw only those forces by arrows which are experienced by the body. We don’t draw those forces that are applied by the body or not acting on the body.
Complete step by step solution:
Given that the elevator is going up with an acceleration of g/10.
Free body diagram (FBD) is a diagram showing all forces acting on a body using arrows, considering body as a point mass.
FBD of the given situation is shown below:
Tension (T): It is an internal molecular force which appear in a string when it is taunt by some external force. Force of tension always acts along the length of the string. Force of tension always act along the length of the string. Direction of tension is always away from the tied ends or points of contact of string. It always has pulling tendency.
Here, $\dfrac{{{{{m}}_{{A}}}{{g}}}}{{{{10}}}}$ and $\dfrac{{{{{m}}_{{B}}}{{g}}}}{{{{10}}}}$are pseudo force.
Let us consider that mass of body A is 3 kg and mass of body B is 1.5 kg (as per given figure)
For body A
${{{m}}_{{A}}}{{a = T - }}{{{m}}_{{A}}}{{g - }}\dfrac{{{{{m}}_{{A}}}{{g}}}}{{{{10}}}}...{{(i)}}$
For body B
${{{m}}_{{B}}}{{a = }}{{{m}}_{{B}}}{{g + }}\dfrac{{{{{m}}_{{B}}}{{g}}}}{{{{10}}}}{{ - T}}...{{(ii)}}$
Adding equations (i) and (ii), we get
$
{{{m}}_{{A}}}{{a + }}{{{m}}_{{B}}}{{a = T - }}{{{m}}_{{A}}}{{g - }}\dfrac{{{{{m}}_{{A}}}{{g}}}}{{{{10}}}}{{ + }}{{{m}}_{{B}}}{{g + }}\dfrac{{{{{m}}_{{B}}}{{g}}}}{{{{10}}}}{{ - T}} \\
\Rightarrow {{(}}{{{m}}_{{A}}}{{ + }}{{{m}}_{{B}}}{{)a = (}}{{{m}}_{{B}}}{{ - }}{{{m}}_{{A}}}{{)g + (}}{{{m}}_{{B}}}{{ - }}{{{m}}_{{A}}}{{)}}\dfrac{{{g}}}{{{{10}}}} \\
$
As ${{{m}}_{{A}}}{{ = 1}}{{.5 kg}}$ and ${{{m}}_{{B}}}{{ = 3 kg}}$
On substituting the values of masses ${{{m}}_{{A}}}$and ${{{m}}_{{B}}}$in above equation, we get
$
{{(1}}{{.5 + 3)a = (3 - 1}}{{.5)g + (3 - 1}}{{.5)}}\dfrac{{{g}}}{{{{10}}}} \\
\Rightarrow 4.{{5a = 1}}{{.5g - 1}}{{.5}}\dfrac{{{g}}}{{{{10}}}} \\
\Rightarrow {{4}}{{.5a = 1}}{{.5g}}\left( {{{1 - }}\dfrac{{{1}}}{{{{10}}}}} \right) \\
\Rightarrow {{4}}{{.5a = 1}}{{.5g \times }}\dfrac{{{9}}}{{{{10}}}} \\
\therefore \dfrac{{{a}}}{{{g}}}{{ = }}\dfrac{{{3}}}{{{{10}}}} \\
$
Now using equation (i), we get
$
{{{m}}_{{A}}}{{a = T - }}{{{m}}_{{A}}}{{g - }}\dfrac{{{{{m}}_{{A}}}{{g}}}}{{{{10}}}} \\
{{Or }} \\ T= {{{m}}_{{A}}}{{(a + g + }}\dfrac{{{g}}}{{{{10}}}}{{)}} \\
$
Reading of the spring balance is given by
$
\dfrac{{{{2T}}}}{{{g}}}{{ = }}\dfrac{{{2}}}{{{g}}}{{{m}}_{{A}}}{{(a + g + }}\dfrac{{{g}}}{{{{10}}}}{{)}} \\
{{Or }} \\ \dfrac{{{{2T}}}}{{{g}}}{{ = 2 \times 1}}{{.5}}\left( {\dfrac{{{a}}}{{{g}}}{{ + 1 + }}\dfrac{{{1}}}{{{{10}}}}} \right) \\
\Rightarrow {{3}}\left( {\dfrac{{{3}}}{{{{10}}}}{{ + 1 + }}\dfrac{{{1}}}{{{{10}}}}} \right){{ = 3(0}}{{.3 + 1 + 0}}{{.1) = 4}}{{.2 Kg}} \\
$
The reading of the spring balance will be 4.2 Kg.
Note: In free body diagram, we draw only those forces by arrows which are experienced by the body. We don’t draw those forces that are applied by the body or not acting on the body.
Recently Updated Pages
JEE Main 2023 April 6 Shift 1 Question Paper with Answer Key

JEE Main 2023 April 6 Shift 2 Question Paper with Answer Key

JEE Main 2023 (January 31 Evening Shift) Question Paper with Solutions [PDF]

JEE Main 2023 January 30 Shift 2 Question Paper with Answer Key

JEE Main 2023 January 25 Shift 1 Question Paper with Answer Key

JEE Main 2023 January 24 Shift 2 Question Paper with Answer Key

Trending doubts
JEE Main 2026: Session 2 Registration Open, City Intimation Slip, Exam Dates, Syllabus & Eligibility

JEE Main 2026 Application Login: Direct Link, Registration, Form Fill, and Steps

Understanding the Angle of Deviation in a Prism

Hybridisation in Chemistry – Concept, Types & Applications

How to Convert a Galvanometer into an Ammeter or Voltmeter

Understanding Uniform Acceleration in Physics

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Laws of Motion Class 11 Physics Chapter 4 CBSE Notes - 2025-26

Waves Class 11 Physics Chapter 14 CBSE Notes - 2025-26

Mechanical Properties of Fluids Class 11 Physics Chapter 9 CBSE Notes - 2025-26

Thermodynamics Class 11 Physics Chapter 11 CBSE Notes - 2025-26

Units And Measurements Class 11 Physics Chapter 1 CBSE Notes - 2025-26




