Question

Find the locus of the intersection of tangents to the parabola \[{{y}^{2}}=4ax\], the angle between them being always a given angle \[\alpha \].

Answer 1

Hint: If \[\alpha \] is the angle between two lines having slopes \[{{m}_{1}}\] and \[{{m}_{2}}\], then
\[\tan \alpha =\left| \dfrac{{{m}_{1}}-{{m}_{2}}}{1+{{m}_{1}}{{m}_{2}}} \right|\]
 The given equation of the parabola is \[{{y}^{2}}=4ax\].

We will consider two points \[A\left( at_{1}^{2},2a{{t}_{1}} \right)\] and \[B\left( at_{2}^{2},2a{{t}_{2}} \right)\] on the parabola , where \[{{t}_{1}}\] and \[{{t}_{2}}\] are parameters.

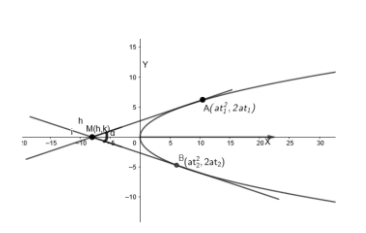
We need to find the equation of tangents at these points.
Now , we know the general equation of tangent at \[\left( a{{t}^{2}},2at \right)\] is given by \[ty=x+a{{t}^{2}}\], where \[t\] is a parameter .
So , the equation of tangent at \[A\left( at_{1}^{2},2a{{t}_{1}} \right)\] is given by substituting \[{{t}_{1}}\] in place of \[t\] in the general equation of tangent .
On substituting \[{{t}_{1}}\] in place of \[t\] in the general equation of tangent , we get
\[{{t}_{1}}y=x+at_{1}^{2}.....\left( i \right)\]
Similarly , the equation of tangent at \[B\left( at_{2}^{2},2a{{t}_{2}} \right)\] is given as
\[{{t}_{2}}y=x+at_{2}^{2}.....\left( ii \right)\]
Now, we need to find their point of intersection . To find the point of intersection , we will substitute the value of \[x\] from equation \[\left( i \right)\] in equation \[\left( ii \right)\].
From \[\left( i \right)\], we have
\[{{t}_{1}}y=x+at_{1}^{2}\]
\[\Rightarrow x={{t}_{1}}\left( y-a{{t}_{1}} \right)....\left( iii \right)\]
On substituting the value of \[x\] in equation \[\left( ii \right)\], we get
\[{{t}_{2}}y={{t}_{1}}\left( y-a{{t}_{1}} \right)+at_{2}^{2}\]
\[\Rightarrow \left( {{t}_{2}}-{{t}_{1}} \right)y=-at_{1}^{2}+at_{2}^{2}\]
\[\Rightarrow \left( {{t}_{2}}-{{t}_{1}} \right)y=\left( {{t}_{2}}-{{t}_{1}} \right)\left( {{t}_{2}}+{{t}_{1}} \right)a\]
\[\Rightarrow y=a\left( {{t}_{1}}+{{t}_{2}} \right).....\left( iv \right)\]
Now , we will substitute \[y=a\left( {{t}_{1}}+{{t}_{2}} \right)\] in equation \[\left( iii \right)\].
On substituting \[y=a\left( {{t}_{1}}+{{t}_{2}} \right)\] in equation \[\left( iii \right)\], we get
\[x={{t}_{1}}\left( a{{t}_{1}}+a{{t}_{2}}-a{{t}_{1}} \right)\]
\[\Rightarrow x=a{{t}_{1}}{{t}_{2}}....\left( v \right)\]
Now , we need to find the locus of the point of intersection.
So , let the point of intersection be\[M\left( h,k \right)\].
Now , from equation \[\left( i \right)\], we can see that the slope of tangent is \[{{m}_{1}}=\dfrac{1}{{{t}_{1}}}\].
From equation \[\left( ii \right)\], we can see that the slope of tangent is \[{{m}_{2}}=\dfrac{1}{{{t}_{2}}}\].
Now , we know if \[\theta \] is the angle between two lines with slope \[{{m}_{1}}\] and \[{{m}_{2}}\] then ,
\[\tan \theta =\dfrac{{{m}_{2}}-{{m}_{1}}}{1+{{m}_{1}}{{m}_{2}}}\]
Now , in the question it is given that the tangents include angle \[\alpha \].
So , \[\tan \alpha =\dfrac{\dfrac{1}{{{t}_{1}}}-\dfrac{1}{{{t}_{2}}}}{1+\left( \dfrac{1}{{{t}_{1}}}.\dfrac{1}{{{t}_{2}}} \right)}\]
\[\tan \alpha =\dfrac{{{t}_{2}}-{{t}_{1}}}{{{t}_{2}}{{t}_{1}}+1}\]

Now , we will square both sides .
On squaring both sides , we get
\[\left( {{\tan }^{2}}\alpha \right){{\left( {{t}_{2}}{{t}_{1}}+1 \right)}^{2}}={{\left( {{t}_{2}}-{{t}_{1}} \right)}^{2}}\]
\[\Rightarrow \left( {{\tan }^{2}}\alpha \right){{\left( {{t}_{2}}{{t}_{1}}+1 \right)}^{2}}={{\left( {{t}_{1}}+{{t}_{2}} \right)}^{2}}-4{{t}_{1}}{{t}_{2}}....\left( vi \right)\]
Now , we know \[M\left( h,k \right)\] is the point of intersection.
So , from equation \[\left( iv \right)\] and equation\[\left( v \right)\] , we get
 \[h=a{{t}_{1}}{{t}_{2}}\Rightarrow {{t}_{1}}{{t}_{2}}=\dfrac{h}{a}\]
\[k=a\left( {{t}_{1}}+{{t}_{2}} \right)\Rightarrow {{t}_{1}}+{{t}_{2}}=\dfrac{k}{a}\]
Now , we will substitute the values of \[{{t}_{1}}{{t}_{2}}\] and \[\left( {{t}_{1}}+{{t}_{2}} \right)\] in equation \[\left( vi \right)\].
On substituting the values of \[{{t}_{1}}{{t}_{2}}\] and \[\left( {{t}_{1}}+{{t}_{2}} \right)\] in equation \[\left( vi \right)\], we get
\[\left( {{\tan }^{2}}\alpha \right){{\left( \dfrac{h}{a}+1 \right)}^{2}}={{\left( \dfrac{k}{a} \right)}^{2}}-\dfrac{4h}{a}\]
\[\Rightarrow \left( {{\tan }^{2}}\alpha \right){{\left( h+a \right)}^{2}}={{k}^{2}}-4ah........\]equation\[(vii)\]
Now, to find the locus of \[M\left( h,k \right)\], we will substitute \[(x,y)\] in place of \[(h,k)\] in equation \[(vii)\].
So , the locus of \[M\left( h,k \right)\] is given as \[\left( {{\tan }^{2}}\alpha \right){{\left( x+a \right)}^{2}}={{y}^{2}}-4ax\]

Note: : While simplifying the equations , please make sure that sign mistakes do not occur. These mistakes are very common and can cause confusions while solving. Ultimately the answer becomes wrong. So, sign conventions should be carefully taken .