Question

Find number of value of $x\in \left[ -2\pi ,2\pi \right]$, If ${{\log }_{0.5}}\sin x=1-{{\log }_{0.5}}\cos x$.

Answer 1

Hint: Use property of logarithm that is \[{{\log }_{a}}a=1\]and ${{\log }_{c}}a-{{\log }_{c}}b={{\log }_{c}}\left( \dfrac{a}{b} \right)$to simplify the given relation. Use a graphical approach to find values of ‘x’ for simplicity.

Complete step-by-step answer:
Here, it is given that ${{\log }_{0.5}}\sin x=1-{{\log }_{0.5}}\cos x$, and then we need to determine all the values of x lying in$\left[ -2\pi ,2\pi \right]$.
We have
${{\log }_{0.5}}\sin x=1-{{\log }_{0.5}}\cos x\ldots \ldots (1)$
As we know the property of the logarithm function that \[{{\log }_{a}}a=1\] where $a>0$and $a\ne 1$.
Or vice-versa is also true. It means we can replace ‘1’ from equation (1) by \[{{\log }_{0.5}}0.5\]for the simplification of the problem.
Hence, equation (1) can be written as
${{\log }_{0.5}}\sin x={{\log }_{0.5}}0.5-{{\log }_{0.5}}\cos x$
We can use property of logarithm ${{\log }_{c}}a-{{\log }_{c}}b={{\log }_{c}}\left( \dfrac{a}{b} \right)$, with the above equation and get
${{\log }_{0.5}}\sin x={{\log }_{0.5}}\left( \dfrac{0.5}{\cos x} \right)\ldots \ldots (2)$
As we know that ‘a’ should be equal to ‘b’ if ${{\log }_{c}}a={{\log }_{c}}b$.
Hence, using the above property with equation (2), we get
$\dfrac{\sin x}{1}=\dfrac{0.5}{\cos x}$
On cross-multiplying, we get
$\sin x\cos x=\dfrac{1}{2}$or $2\sin x\cos x=1\ldots \ldots (3)$
As we know the trigonometric identity of $\sin 2x$as $\sin 2x=2\sin x\cos x$or vice-versa.
Hence, equation (3) can be given as
$\sin 2x=1\ldots \ldots (4)$
Now, we have to find ‘x’ in the interval$\left[ -2\pi ,2\pi \right]$.
So we have $-2\pi \le x\le 2\pi $
Multiplying by ‘2’ on each side we get
$-4\pi \le 2x\le 4\pi $
Now, drawing graph of $\sin x$ from $-4\pi $ to \[4\pi \], we get

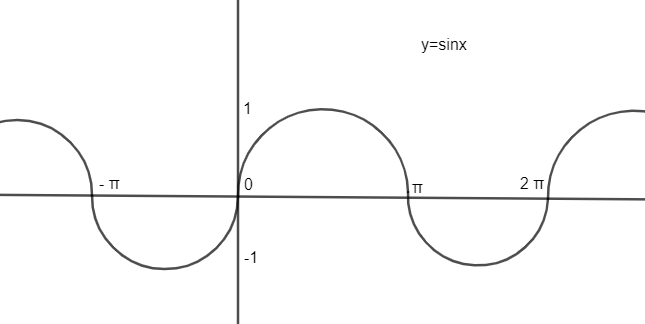
As we can observe that $y=\sin x$ has values of 1 at $\dfrac{\pi }{2},\dfrac{5\pi }{2},\dfrac{-3\pi }{2},\dfrac{-7\pi }{2}$.
Now, we have the equation $\sin 2x=1$.
Hence,
$2x=\dfrac{-7\pi }{2},\dfrac{-3\pi }{2},\dfrac{\pi }{2}.\dfrac{5\pi }{2}$
Or $x=\dfrac{-7\pi }{4},\dfrac{-3\pi }{4},\dfrac{\pi }{4}.\dfrac{5\pi }{4}$

Note: One can get confusion between $y=\sin x$ and equation $\sin 2x=1$. Graph of $y=\sin x$ is representing the general relation between angles and values which is not related to equation$\sin 2x=1$. One can suppose ‘2x’ as ‘t’ as well for the simplicity, so we will get equation $\sin t=1$. Now, t will lie in $\left[ -4\pi ,4\pi \right]$ as \[t=2x\]; hence find all values of ‘t’ then find ‘x’ by using relation $x=\dfrac{t}{2}$.