Question

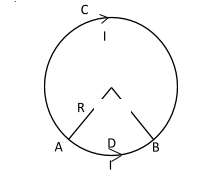
Equal current I flows in two segments of a circular loop in the direction shown in figure. Radius of the loop is a. Magnetic field at the center of the loop is

Answer 1

Hint: A magnetic field is a vector field that describes the magnetic influence on moving electric charge, electric currents, and magnetic materials. A moving charge in a magnetic field experiences a force perpendicular to its own velocity and to the magnetic field. Magnetic fields are represented using magnetic lines. It is a visual tool used to visualize the direction.

Complete answer:
Flow of current I
As we know that magnetic field of circular loop is given by,
$ B = \dfrac{{{\mu _o}I}}{{2R}}$
Here,
I=electric current
R=Radius of circular loop
Magnetic field due to ADB
$ \Rightarrow {B_1} = \left( {\dfrac{\theta }{{2\pi }}} \right)\dfrac{{{\mu _o}I}}{{2R}}$ …(1)
Perpendicular to paper outwards
Now,
And magnetic field due to ACB
$ \Rightarrow {B_2} = \left( {\dfrac{{2\pi - \theta }}{{2\pi }}} \right)\dfrac{{{\mu _o}I}}{{2R}}$ …(2)
Perpendicular to paper inwards
Net magnetic field is given by
$ {B_{net}} = {B_2} - {B_1}$
Put the value
     \[\Rightarrow {B_{net}} = \left( {\dfrac{{2\pi - \theta }}{{2\pi }}} \right)\dfrac{{{\mu _o}I}}{{2R}} - \left( {\dfrac{\theta }{{2\pi }}} \right)\dfrac{{{\mu _o}I}}{{2R}}\]
Simplify
\[ \Rightarrow {B_{net}} = \left( {\dfrac{{2\pi - \theta }}{{2\pi }} - \dfrac{\theta }{{2\pi }}} \right)\dfrac{{{\mu _o}I}}{{2R}}\]
\[ \Rightarrow {B_{net}} = \left( {\dfrac{{2\pi - 2\theta }}{{2\pi }}} \right)\dfrac{{{\mu _o}I}}{{2R}}\]
\[ \Rightarrow {B_{net}} = \left( {\dfrac{{\pi - \theta }}{\pi }} \right)\dfrac{{{\mu _o}I}}{{2R}}\]

Note: The closeness or density of the field lines is directly proportional to the strength of the field. Magnetic field lines appear to emerge or start from the north pole and merge or terminate at the south pole. Inside the magnet, the direction of the magnetic field lines is from the south pole to the north pole. Magnetic field lines never intersect with each other. Magnetic field lines form a closed-loop.