Question

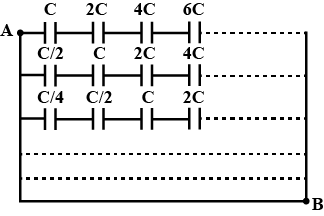
Consider an infinite matrix of capacitors as shown in the figure. The effective capacitance between point A and point B will be:

$(a)C$
$(b)2C$
$(c)\infty $
$(d)$ can’t be determined

Answer 1

Hint: Since A and B are connected in parallel, we will first calculate capacitance in all the rows. Once, capacitance in all the rows is known then the whole system becomes a problem, in which all the capacitances are parallel to each other in a vertical order. Thus, the final capacitance can be known by adding these individual capacitances.

Complete answer:
In all the respective row, the capacitors are in series, therefore their capacitance can be calculated by adding the sum of their individual inverse, i.e.,
$\begin{align}
  & \Rightarrow \dfrac{1}{{{C}_{R1}}}=\left[ \dfrac{1}{C}+\dfrac{1}{2C}+\dfrac{1}{4C}+\dfrac{1}{6C}..................... \right] \\
 & \Rightarrow \dfrac{1}{{{C}_{R1}}}=\dfrac{1}{C}+\dfrac{1}{C}\left[ \dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{6}......................... \right] \\
 & \\
\end{align}$
Here, we can clearly see that the term inside the bracket is a converging series. So, it has a finite value. Let us see if we can calculate the sum of this series.
The given series : $\left[ \dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{6}......................... \right]$ is a Harmonic Progression whose sum cannot be calculated. The only comment that can be made about this Harmonic Series is that it has a finite value.
Thus, the sum of the first row is finite but cannot be determined.
Therefore, even though the sum of the rest of the horizontal rows can be calculated using the sum formula of infinite Geometric Progression, the sum of the first row will still be unknown but finite.
Hence, the net capacitance of the given infinite series is finite but cannot be determined.

Hence, option $(d)$ is the correct option.

Note:
If the problem had capacitance as $8C$in place of $6C$ , the first row then too would have been a case of infinite Geometric progression and then the whole problem would be solvable. But, at times there can be printing errors while giving exams even at the national level, so one should not modify the question and first check if any option satisfies the answer.