
Consider a body of 800 kg moving with a maximum speed $v$ on a road banked at\[\theta = {30^0}\] given \[\cos {30^0} = 0.87\]. Find the normal reaction on the body. Coefficient of friction \[{\mu _s} = 0.2\]. [Take radius, r=10m]
A. 10.4 kN
B. 12.6 kN
C. 11.6 kN
D. 8.3 kN
Answer
233.1k+ views
Hint:When the applied force increases, then the force of friction also increases. The maximum value of static friction is known as limiting friction.
If a body is moving with a maximum speed v on a road banked. Since the circular motion is such that v = vmax the tendency of the body is to move up the inclined plane.
Formula used:
Centripetal force is given as:
\[\dfrac{{m{v^2}}}{r}\]
Where m is the mass of the given body, r is the radius of the circle and v is the maximum speed.
Maximum friction,
\[{f_s} = {\mu _s}N\]
Where \[{\mu _s}\]is the coefficient of friction and N is the normal reaction between the two surfaces.
Complete step by step solution:
Given Coefficient of friction \[{\mu _s} = 0.2\].
Radius of circle, r=10m
\[\cos {30^0} = 0.87\]
Taking g=10m/\[{s^2}\]
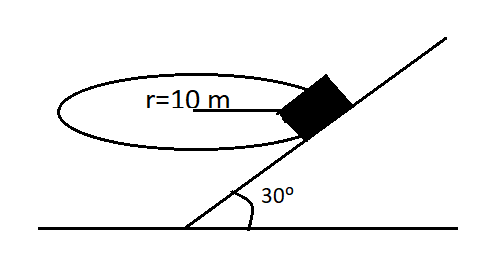
In a body force mg is in downward direction and normal reaction is along incline. Here the incline is in \[{30^0}\](in figure). The friction force is along incline and it is at maximum because it moves its maximum speed. Also a centrifugal force acts on it in an outward direction.
Now the normal reaction will be applied perpendicular to the inclined.
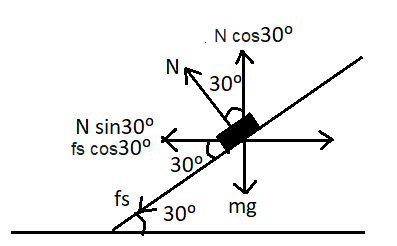
Image: Diagram showing resolving components.
After resolving along X axis and Y axis, we have
\[N\cos {30^0} = mg + {f_s}\sin {30^0}\]
As we know, maximum friction \[{f_s} = {\mu _s}N = 0.2N\]
Substituting all the values, we get
\[N\cos {30^0} = mg + {f_s}\sin {30^0}\]
\[\begin{array}{l} \Rightarrow N \cos {30^0} = mg + {f_s}\sin {30^0}\\0.87{\rm{ N = 800}} \times {\rm{10 + 0}}{\rm{.2N}} \times \dfrac{1}{2}\\ \Rightarrow N = \dfrac{{800}}{{0.77}}\\\Rightarrow N {\rm{ = }}10389.6{\rm{ N}}\\ \Rightarrow N {\rm{ = 10400 N}}\\ \therefore N {\rm{ }} \approx {\rm{ 10}}{\rm{.4 kN}}\end{array}\]
Therefore the normal reaction on the body is 10.4 kN.
Hence option A is the correct answer
Note: The banking of roads is the phenomenon in which the outer edges must curve roads above the inner edge to provide the centripetal force to the vehicles so that they can take safe turns.
If a body is moving with a maximum speed v on a road banked. Since the circular motion is such that v = vmax the tendency of the body is to move up the inclined plane.
Formula used:
Centripetal force is given as:
\[\dfrac{{m{v^2}}}{r}\]
Where m is the mass of the given body, r is the radius of the circle and v is the maximum speed.
Maximum friction,
\[{f_s} = {\mu _s}N\]
Where \[{\mu _s}\]is the coefficient of friction and N is the normal reaction between the two surfaces.
Complete step by step solution:
Given Coefficient of friction \[{\mu _s} = 0.2\].
Radius of circle, r=10m
\[\cos {30^0} = 0.87\]
Taking g=10m/\[{s^2}\]

In a body force mg is in downward direction and normal reaction is along incline. Here the incline is in \[{30^0}\](in figure). The friction force is along incline and it is at maximum because it moves its maximum speed. Also a centrifugal force acts on it in an outward direction.
Now the normal reaction will be applied perpendicular to the inclined.

Image: Diagram showing resolving components.
After resolving along X axis and Y axis, we have
\[N\cos {30^0} = mg + {f_s}\sin {30^0}\]
As we know, maximum friction \[{f_s} = {\mu _s}N = 0.2N\]
Substituting all the values, we get
\[N\cos {30^0} = mg + {f_s}\sin {30^0}\]
\[\begin{array}{l} \Rightarrow N \cos {30^0} = mg + {f_s}\sin {30^0}\\0.87{\rm{ N = 800}} \times {\rm{10 + 0}}{\rm{.2N}} \times \dfrac{1}{2}\\ \Rightarrow N = \dfrac{{800}}{{0.77}}\\\Rightarrow N {\rm{ = }}10389.6{\rm{ N}}\\ \Rightarrow N {\rm{ = 10400 N}}\\ \therefore N {\rm{ }} \approx {\rm{ 10}}{\rm{.4 kN}}\end{array}\]
Therefore the normal reaction on the body is 10.4 kN.
Hence option A is the correct answer
Note: The banking of roads is the phenomenon in which the outer edges must curve roads above the inner edge to provide the centripetal force to the vehicles so that they can take safe turns.
Recently Updated Pages
JEE Main 2023 April 6 Shift 1 Question Paper with Answer Key

JEE Main 2023 April 6 Shift 2 Question Paper with Answer Key

JEE Main 2023 (January 31 Evening Shift) Question Paper with Solutions [PDF]

JEE Main 2023 January 30 Shift 2 Question Paper with Answer Key

JEE Main 2023 January 25 Shift 1 Question Paper with Answer Key

JEE Main 2023 January 24 Shift 2 Question Paper with Answer Key

Trending doubts
JEE Main 2026: Session 2 Registration Open, City Intimation Slip, Exam Dates, Syllabus & Eligibility

JEE Main 2026 Application Login: Direct Link, Registration, Form Fill, and Steps

JEE Main Marking Scheme 2026- Paper-Wise Marks Distribution and Negative Marking Details

Understanding the Angle of Deviation in a Prism

Hybridisation in Chemistry – Concept, Types & Applications

How to Convert a Galvanometer into an Ammeter or Voltmeter

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Laws of Motion Class 11 Physics Chapter 4 CBSE Notes - 2025-26

Waves Class 11 Physics Chapter 14 CBSE Notes - 2025-26

Mechanical Properties of Fluids Class 11 Physics Chapter 9 CBSE Notes - 2025-26

Thermodynamics Class 11 Physics Chapter 11 CBSE Notes - 2025-26

Units And Measurements Class 11 Physics Chapter 1 CBSE Notes - 2025-26




