Question

Calculate the potential difference and the energy stored in the capacitor \[{C_2}\] in the circuit shown in the figure. Given potential at A is \[90V\] , \[{C_1} = 20\mu F\] \[{C_2} = 30\mu F\] and \[{C_3} = 15\mu F\]

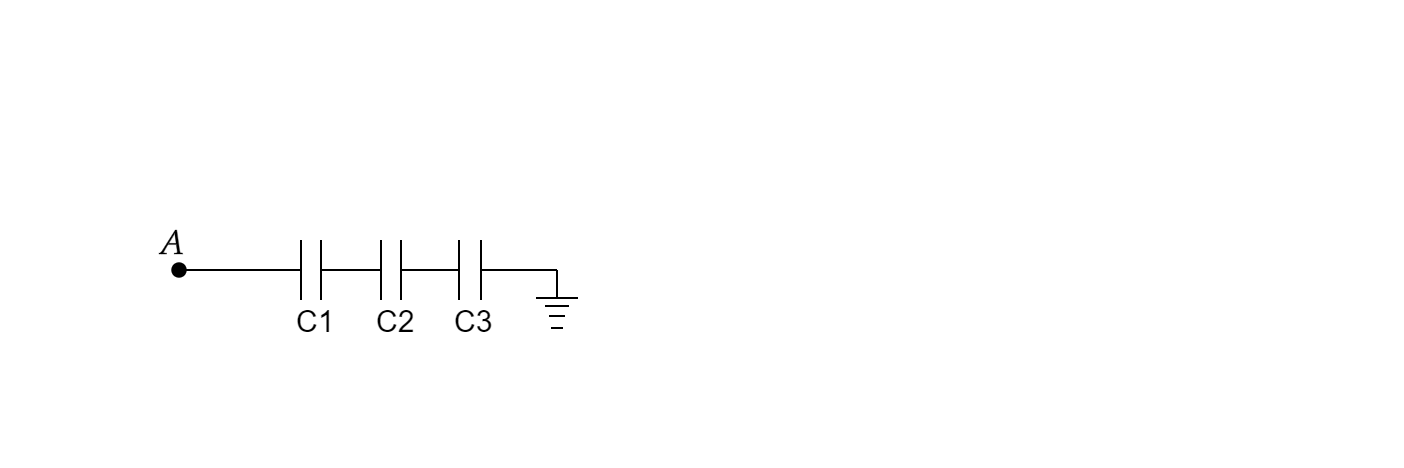
Answer 1

Hint:To find the energy stored in any capacitor, we need to know the value of the capacitance of the capacitor and the potential difference across its plates. We have been given the potential difference across the entire setup of capacitors but we need to find the energy stored only in the capacitor \[{C_2}\] , so firstly, we need to find the potential difference across \[{C_2}\] and then proceed as follows.

Complete step-by-step solution:
Firstly, resolve the given system of capacitors into a single capacitor by finding the equivalent capacitance of the system.
\[\dfrac{1}{{{C_{eq}}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}} + \dfrac{1}{{{C_3}}}\]
\[\therefore \dfrac{1}{{{C_{eq}}}} = \dfrac{1}{{20}} + \dfrac{1}{{30}} + \dfrac{1}{{15}}\] \[ \Rightarrow \dfrac{1}{{{C_{eq}}}} = \dfrac{9}{{60}} \Rightarrow {C_{eq}} = 6.67\mu F\]
This means that charge flowing through the circuit \[Q = {C_{eq}}V = 6.67\mu F \times 90V = 600\mu C\]
Now let’s consider our capacitor \[{C_2}\] ,
The charge flowing through this capacitor will be the same as charge flowing through the setup of capacitors, hence \[Q = {C_2}{V_{_2}} \Rightarrow {V_{_2}} = \dfrac{Q}{{{C_2}}} = \dfrac{{600}}{{30}} = 20V\]
Now we know the potential difference across \[{C_2}\] and its capacitance, so we can easily find the energy stored in it.
Energy of the capacitor $(E) = \dfrac{1}{2}C{V^2}$
By substituting the values in the formula, we get
\[{E_2} = \dfrac{1}{2}{C_2}{V_{_2}}^2 = \dfrac{1}{2} \times 30\mu F \times {(20V)^2} = 6 \times {10^{ - 3}}J\]

Additional Information:
For solving questions having a combination of capacitors or resistors, we need to find the physical quantity that remains the same throughout the entire system, for example, in a series combination of capacitors, charge flowing through the circuit remains the same. Similarly, for a series combination of resistors, the current through the circuit remains constant and for a parallel combination, the potential difference across each component remains the same. Once we have found the constant quantity, we can easily divide current, potential, charge or energy among the individual components.

Note:- One common error made by students is that while calculating energy, they use the equivalent capacitance of the circuit instead of the capacitance of the specific capacitor whose energy is to be calculated. Make sure not to make that error.