Question

Calculate the electric current in the circuit shown.

Answer 1

Hint: In order to solve this question, we are firstly going to find the equivalent resistance for the given circuit by telling whether the two resistances are in series combination or the parallel one. After that the total voltage of the circuit is taken along with equivalent resistance to find the electric current.

Formula used: The formula for the equivalent resistance of the resistors in parallel is given by the formula:
\[{R_{eq}} = {R_1} + {R_2}\]
The electric current in the circuit shown is given by the formula
\[i = \dfrac{V}{{{R_{eq}}}}\]
Where \[V\] is the voltage of the circuit as given.

Complete step by step answer:
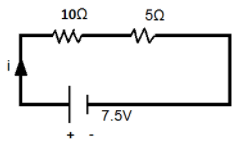
The amount of the current passing through the resistor of resistance \[10\Omega \] will also pass through the resistor of the resistance \[5\Omega \]. Thus, this means that the two resistors are connected in series with each other.
We know that the formula for the equivalent resistance of the resistors in parallel is given by the formula:
\[{R_{eq}} = {R_1} + {R_2}\]
Therefore, their equivalent resistance is equal to
\[{R_{eq}} = 10\Omega + 5\Omega = 15\Omega \]
Thus, the electric current in the circuit shown is given by the formula
\[i = \dfrac{V}{{{R_{eq}}}}\]
Where, \[V\] is the voltage of the circuit as shown .
Thus, putting the values to get the electric current.
\[i = \dfrac{{7.5}}{{15}} = 0.5A\]

Note: It is important to note that in a circuit that consists of the resistors in series they have the same amount of the current passing through all the resistors and the voltage is different. While for the resistors in parallel, the current passing through all is different and the voltages are the same.