Question

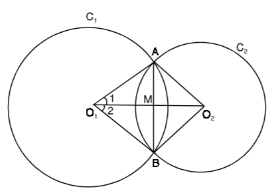
\[{{C}_{1}}\]and \[{{C}_{2}}\] are two circles with center \[{{O}_{1}}\] and \[{{O}_{2}}\] and intersect each other at points \[A\]and \[B\]. If \[{{O}_{1}}{{O}_{2}}\] intersect\[AB\] at\[M\] then show that \[\Delta {{O}_{1}}A{{O}_{2}}\cong \Delta {{O}_{1}}B{{O}_{2}}\]

Answer 1

Hint: We will try to show the two triangles \[\Delta {{O}_{1}}AB\] and \[\Delta {{O}_{2}}AB\] congruent using ‘SSS’ type of triangle congruence.

Given that two circles \[{{C}_{1}}\]and \[{{C}_{2}}\] with center \[{{O}_{1}}\]and \[{{O}_{2}}\] intersect each other at points \[A\]and \[B\].
Also, \[{{O}_{1}}{{O}_{2}}\] intersects \[AB\] at \[M\].
Then, we have to show that \[\Delta {{O}_{1}}A{{O}_{2}}\cong \Delta {{O}_{1}}B{{O}_{2}}\]

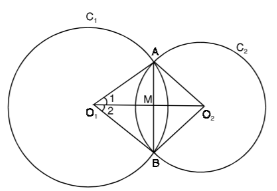
Let us assume that the radius of the circle \[{{C}_{1}}\]be \[r\] and the radius of the circle \[{{C}_{2}}\] be \[s\].
Proof:
In \[\Delta {{O}_{1}}A{{O}_{2}}\] and \[\Delta {{O}_{1}}B{{O}_{2}}\], we have
\[{{O}_{1}}A={{O}_{1}}B.....\left( i \right)\]
Both are radii of the same circle \[{{C}_{1}}\].
\[\Rightarrow {{O}_{2}}A={{O}_{2}}B.....\left( ii \right)\]
Both are radii of the same circle \[{{C}_{2}}\].
Also, \[{{O}_{1}}{{O}_{2}}={{O}_{2}}{{O}_{1}}....\left( iii \right)\]
Common sides of \[\Delta {{O}_{1}}A{{O}_{2}}\] and \[\Delta {{O}_{1}}B{{O}_{2}}\]
So, from equation \[\left( i \right),\left( ii \right)\]and\[\left( iii \right)\], we get both triangles \[\Delta {{O}_{1}}A{{O}_{2}}\]and \[\Delta {{O}_{1}}B{{O}_{2}}\] are congruent with each other by ‘SSS’ type if triangle congruence.
Or,\[\Delta {{O}_{1}}A{{O}_{2}}\cong \Delta {{O}_{1}}B{{O}_{2}}\] by SSS type of triangle congruence.
(Here, ‘SSS’ type means side – side – side type of triangle congruence)
SSS – Theorem

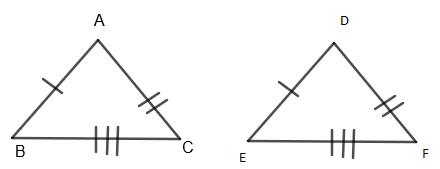
Side - side - side postulate (SSS) states that two triangles are congruent if three sides of one triangle are congruent to the corresponding sides of the other triangle.
Here, from \[\Delta ABC\] and \[\Delta DEF\], we can say that
\[AB=DF....\left( a \right)\]
\[AC=DE....\left( b \right)\]
\[BC=EF....\left( c \right)\]
So, from equation \[\left( a \right),\left( b \right)\] and \[\left( c \right)\], we have \[\Delta ABC\cong \Delta DEF\] by SSS – type triangle congruence.

Note: Visualize the geometry first before attempting the question. Make a clear diagram of the required question which reduces the probability of error in your solution. Using the SSS theorem, we prove the congruence of the required triangles to prove what is given.