Question

An inductor and resistor are connected in series with an AC source. In this circuit,
The current and the PD across resistance lead the PD across the inductance.
(A) The current and the PD across the resistance lag behind the PD across the inductance by angle $\dfrac{\pi }{2}$
(B) The current and the PD across the resistance lag behind the PD across the inductance by an angle $\pi $
(C) The PD across the resistance lags behind the PD across the inductance by an angle (D)$\dfrac{\pi }{2}$ but the current in resistance leads the PD across the inductance by $\dfrac{\pi }{2}$.

Answer 1

Hint Find the impedance for series resistance and inductor AC circuit then, draw the phasor diagram of series inductance and resistance series AC circuit. In the phasor diagram, draw the voltage across resistance and also draw the voltage across inductance. If the angle of voltage across inductance is greater then it leads the voltage across resistance.

Step by Step Solution
Let the resistance and inductance be R and L respectively
Construct a series L-R AC circuit

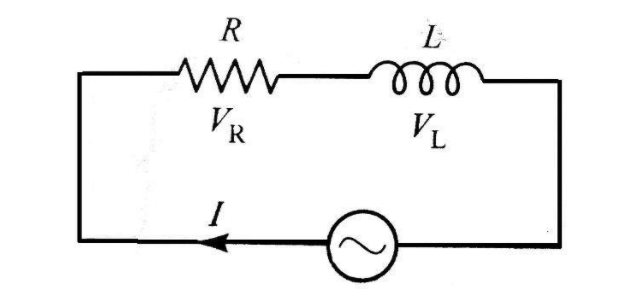
Now, we get
${V_{net}} = {\vec V_L} + {\vec V_R}$
By taking magnitude
\[
  \left| {{{\vec V}_{net}}} \right| = \sqrt {({V^2}_L + {V^2}_R)} \\
  \left| {{{\vec V}_{net}}} \right| = \sqrt {({i^2}{X^2}_L + {i^2}{R^2})} \\
    \\
 \]
By taking ${i^2}$ common
\[\left| {{{\vec V}_{net}}} \right| = i\sqrt {({X^2}_L + {R^2})} \]
To calculate the impedance let impedance be $Z$
$Z = \dfrac{V}{i} = \sqrt {({X_L}^2 + {R^2})} $
Because, ${X_L} = \omega L$ we get
$Z = \sqrt {({\omega ^2}{L^2} + {R^2})} $
This is the impedance for series L-R AC circuit
Now, draw the phasor diagram for series L-R AC circuit

$
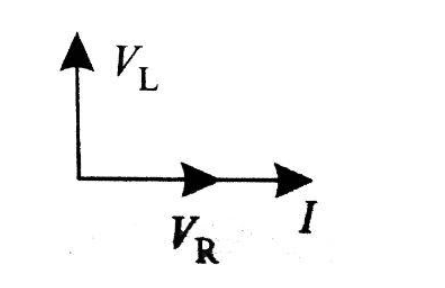
  \tan \varphi = \dfrac{{{V_L}}}{{{V_R}}} \\
  \tan \varphi = \dfrac{{i{X_L}}}{{iR}} \\
    \\
 $
Now, we get
$\varphi = {\tan ^{ - 1}}\left( {\dfrac{{{X_L}}}{R}} \right)$
Therefore, after seeing the phasor diagram we can easily conclude that potential difference across inductance leads the current and potential difference across resistance by an angle $\dfrac{\pi }{2}$

Hence, option (B) is the correct answer.

Note resistance is the measure of the opposition of current in the circuit. It is denoted by R. It is measured in ohms $(\Omega )$.
Inductance is the property of a conductor to oppose the flow of electric current through it. The flow of current makes a magnetic field around the conductor. It is denoted by L. It is measured in Henry $(H)$.