Question

An electric heater which is connected to a 220 V supply line has two resistance coils A and B of 24ohm resistance each. These coils can be used separately (one at a time), in series, or in parallel. Calculate the current drawn when:
(a) only one coil A is used.
(b) Coils A and B are used in series.

Answer 1

Hint: The resistance in the resistance coils and the given voltage can be used in ohm’s law to find how much the current has drawn. When the coils A and B are connected in a series, we just need to find the equivalent resistance in the coils. Then, by using Ohm’s law we can find out how much the current has drawn.


Complete step-by-step solution:
Let us draw an electric circuit, for (a) only one coil A is used.

Now, let the resistance of A be ${R_A}$then the current be${I_1}$ can be found by using ohm's law
$V = {I_1}{R_A} \Rightarrow {I_1} = \dfrac{V}{{{R_A}}}$
$ \Rightarrow {I_1} = \dfrac{{220V}}{{24\Omega }}$
$ \Rightarrow {I_1} = 9.16A$
Therefore, the current drawn by using the electric heater when only one coil A is used is $0.917A$
Next, let us draw the circuit diagram for (b) Coils A and B are used in series.

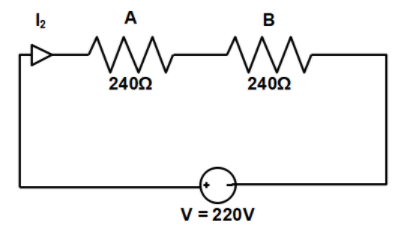
Now, the resistance coils are connected in a series, the equivalent resistance of the circuit coils will be
${R_{eq}} = {R_A} + {R_B}$
$ \Rightarrow {R_{eq}} = 24\Omega + 24\Omega $
$ \Rightarrow {R_{eq}} = 48\Omega $
Let us assume that ${I_2}$is the current drawn when the coils are connected in series, using ohm’s law we have
$V = {I_2}{\operatorname{R} _{eq}}$
$ \Rightarrow {I_2} = \dfrac{v}{{{R_{eq}}}}$
$ \Rightarrow {I_2} = \dfrac{{220V}}{{48\Omega }}$
$\therefore {I_2} = 4.58A$
Therefore, the current drawn when the coils A and B are connected in series is $4.58A$

Note: The resistance coils are used in the electric heaters due to their heat dissipation. Here, let us represent the electric heater as a resistor, here we have only connected with the resistor of the electric heater. This applies to all the problems in heating coils, like an electric kettle.