Question

An aeroplane when flying at a height $2500m$ from the ground passes vertically above another aeroplane. At an instant when the angles of elevation of the two aeroplanes from the same point on the ground are ${45^0}$ and ${30^0}$ respectively, then the vertical distance between the two aeroplanes at that instant is:
$(a){\text{ 1158}}{\text{.5m}}$
$(b){\text{ 1056}}{\text{.5m}}$
$(c){\text{ 1008}}{\text{.5m}}$
$(d){\text{ None of these}}$

Answer 1

Hint: In this question we have to find the vertical distance between the two aeroplanes so firstly draw the pictorial representation using the information provided in the question. Then in order to formulate the required equations which will be formed, use the trigonometric identities to find the answer.

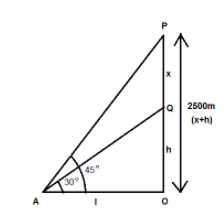
Let us assume $PQ = x$ be the vertical height between the two aeroplanes.
And $OQ = h$ be the vertical height of the second aeroplane from the ground
Such that
$x + h = 2500$ … (1)
We are given that the angles of elevation of the two aeroplanes from the same point on the ground are ${45^0}$ and ${30^0}$.
Now, let us first consider the triangle $OAQ$, we have
$\tan {30^0} = \dfrac{{OQ}}{{0A}}$
$ \Rightarrow \dfrac{1}{{\sqrt 3 }} = \dfrac{h}{l}$
$ \Rightarrow l = \sqrt 3 h$ … (2)
Now, consider the triangle $OAP$, we have
$\tan {45^0} = \dfrac{{OP}}{{0A}}$
$ \Rightarrow \dfrac{{x + h}}{l} = 1$
$ \Rightarrow x + h = l$
Using equation (2), we get
$ \Rightarrow x + h = \sqrt 3 h$ …(3)
Now after equating the equation (1) and equation (3), we get
$ \Rightarrow \sqrt 3 h = 2500$
$ \Rightarrow h = \dfrac{{2500}}{{\sqrt 3 }}$
$ \Rightarrow h = 1443.37m$
After substituting this value in equation (1), we get
$ \Rightarrow x + 1443.37 = 2500$
$ \Rightarrow x = 2500 - 1443.37$
$\therefore x = 1056.63m \approx 1056.5m$
Therefore, the vertical distance between the two aeroplanes at the given distance comes out to be $1056.5m$.
So, the required solution is option $(b){\text{ 1056}}{\text{.5m}}$.

Note: Whenever we face such types of problems, the key point is to have a good understanding of the trigonometric functions like tan, cos, sin, sec etc. After putting the given values in the standard formula of these trigonometric ratios and then equating the results will help you reach the right answer for the problem.