Question

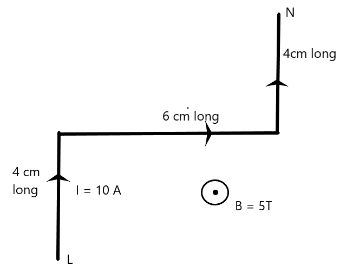
A wire $LN$ bent as shown in figure placed in uniform perpendicular magnetic field of \[5\,T\]. A \[10\,A\] current flows through the wire. Magnetic force experienced by the wire is?

Answer 1

Hint: Force acting on a wire of length \[L\] with current of magnitude \[I\] flowing in it when placed in uniform perpendicular magnetic field is given by the formula \[F=I(L\times B)\]. Use this formula to find the force acting on wire and use vector addition to find the final output.

Complete step by step answer:
Considering the first vertical part of the wire, here direction of length \[L\] is perpendicular to the direction of magnetic field hence angle between them will become ninety degree therefore force magnitude will be,
\[F=I(LB\sin (\frac{\pi }{2})) \\
\Rightarrow F=I(LB)\]

Now let’s find the direction of force, to find the direction point your thumb in the direction of length and rest four fingers towards the direction of the magnetic field. Now the direction of the cross product is normal to your palm. By using this method we will get the direction in positive x direction.
\[F=I(LB)\hat{i}\]

Now considering the horizontal part of the wire, here direction of length $L$ is again perpendicular to the direction of magnetic field but the direction will be different since this time direction of length has changed from positive Y-axis (vertical part) to positive X-axis (horizontal part). Therefore using the above method again this time the force will be
\[F=I({{L}_{1}}B)(-\hat{j})\]
The horizontal part length of the wire is different from the first vertical part.

Now considering the next vertical part, this is similar to that of the first vertical part therefore in this case the force will be the same in magnitude and direction as that of the first vertical part hence \[F=I(LB)\hat{i}\]. Now let’s find the net force using vector addition, two forces are in the same direction hence they will add up simply, while one is perpendicular to it.
\[{{F}_{net}}=2I(LB)\hat{i}-I({{L}_{1}}B)\hat{j}\]
Putting the values of magnetic field, length and current we get ( length in meter)
\[{{F}_{net}}=4\hat{i}-3\hat{j}\]
Now we know for perpendicular system magnitude of force will be square root of sum of squares of its component hence,
\[|{{F}_{net}}|=\sqrt{{{(4)}^{2}}+{{(3)}^{2}}}\]
\[\therefore |{{F}_{net}}|=5\,N\]

Hence the correct option is A.

Note: One can solve this question directly by finding net resultant length and using it in the force equation. This shortcut is helpful since sometimes the question asks to find the force in a closed loop of wire, in this case net length will be zero since the starting point is the same as the ending point which makes net force acting on it zero. However I would suggest avoiding shortcuts and focus more on concepts.