Question

A wall clock uses a simple pendulum and it is accurate at earth surface. If it is taken to a high altitude:
A) It will run fast
B) Its length should be increased to keep it accurate
C) Its length should be decreased to keep it accurate
D) Even if length is changed it cannot be accurate

Answer 1

Hint: Try and recall the factors that the time period of a pendulum depends upon. In other words, we know that the time period is directly proportional to $\sqrt{T}$ and inversely proportional to $\sqrt{g}$.
Now, think of how the acceleration due to gravity g would change for the pendulum if it was taken to an altitude above the surface of the earth. Remember that the force of gravity experienced by a body decreases with increase in height. Depending on your inference here, think of how you can counter the effect with the length of the pendulum using the pendulum’s time period equation.

Formula used:
Time period of a simple pendulum $T = 2\pi\sqrt{\dfrac{L}{g}}$, where L is the length of the string of the pendulum and g is the acceleration due to gravity.
Acceleration due to gravity at a height h from the surface of the earth:
$\Rightarrow g_h = g\left(1+\dfrac{h}{R}\right)^{-2}$, where R is the radius of the earth.

Complete answer:
We know that the time period of a simple pendulum is given as:
$T = 2\pi\sqrt{\dfrac{L}{g}}$, where L is the length of the pendulum’s string and g is the acceleration due to gravity.
Thus, the time period of the pendulum depends on g.
Let us assume that the mass of the pendulum of our wall clock comes entirely from the pendulum bob. To this end, let us look at how the acceleration due to gravity acting on the bob changes with height.
Consider the bob of mass m that is at a height h from the surface of the earth. The force acting on the bob due to gravity is given by the universal law of gravitation:
$F=\dfrac{GMm}{(R+h)^2}$, where R is the radius of the earth, and M is the earth’s mass.

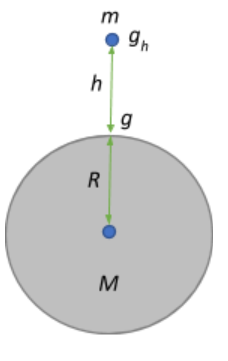
The force due to gravity at a certain height is also given by $mg_h$.
Equating the two $mg_h = \dfrac{GMm}{(R+h)^2} $
$\Rightarrow g_h = \dfrac{GM}{R^2(1+\dfrac{h}{R})^2} $
$\Rightarrow g_h = \left(\dfrac{GM}{R^2}\right)\left( 1+\dfrac{h}{R}\right)^{-2}$
$\Rightarrow g_h = g\left(1+\dfrac{h}{R}\right)^{-2}$
This expression describes the acceleration due to gravity experienced by a body at a certain height h from the surface of the earth. From the above relation we see that the acceleration due to gravity decreases with an increase in height.
Now, from the equation of the time period of the pendulum $T = 2\pi\sqrt{\dfrac{L}{g}}$ we see that since $T \propto \dfrac{1}{\sqrt{g}}$, if g decreases, then T will increase. Thus, to maintain the accuracy of the clock at a high altitude, we counter this decrease in g by decreasing the length of the pendulum’s string since $T \propto \sqrt{L}$.
Thus, the correct option would be C. Its length should be decreased to keep it accurate.

Note: This was a rather quantitative approach to this problem that we’ve taken. However, it is possible to arrive at the same result from a heuristic approach as well. Here, you will still need to know the pendulum’s time period equation, but you can opt out from the $g_h$ calculation by simply thinking in terms of the magnitude of the force of gravity acting between any two bodies with an increasing distance between them. This is given by the Newton’s law of gravitation:
$F = \dfrac{Gm_1m_2}{r^2} \Rightarrow F \propto \dfrac{1}{r^2}$
So if distance between the two bodies increases, then the gravitational force between them decreases. Since we know that $F = mg$, if F decreases it means that g also decreases. From here you can proceed the same way as in the problem to get the T-g-L balance.